 Фролова Е.Д. гр. ПГМ-101 Вариант №9
Лабораторная работа №1
1.1 Задание
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Ввести исходные данные в соответствии с номером варианта.
|
2. Подобрать шаг группирования и выполнить группировку выборки. Записать результат группирования.
|
3. Построить гистограмму частот. Сравнить построенную гистограмму с графиком приведенной плотности нормального распределения.
|
4. Найти выборочные начальные и центральные моменты.
|
5. Указать точечные оценки начальных и центральных моментов, математического ожидания, дисперсии, асимметрии и эксцесса.
|
6. Вычислить доверительные интервалы для математического ожидания и дисперсии для доверительных вероятностей g = 0,9; 0,95; 0,99.
|
7. Проверить соответствие выборки нормальному закону по критерию Хи-квадрат и уровню значимости a = 0,05.
|
8. Включить в отчет о лабораторной работе:
|
– наилучшую группированную выборку;
|
– точечные оценки моментов и других характеристик;
|
– доверительные интервалы для математического ожидания и дисперсии;
|
– гистограмму частот и график приведенной плотности нормального распределения с соответствующими значениями параметров;
|
– выводы о согласии выборочных данных с гипотезой о нормальности распределения генеральной совокупности;
|
– рекомендации о номинальной суточной мощности a нового предприятия и оценку возможных отклонений его суточной нагрузки.
|
1.2 Исходные данные
|
|
Вариант №
|
|
9
|
|
|
Элементы выборки записаны в таблице. Из них будет обработано только первые n =150 элементов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
Номер элемента
|
Элемент выборки
|
1
|
34,51
|
21
|
34,52
|
41
|
34,66
|
61
|
32,96
|
81
|
36,55
|
101
|
34,91
|
121
|
35,22
|
141
|
34,45
|
2
|
32,35
|
22
|
32,99
|
42
|
34,3
|
62
|
32,9
|
82
|
32,81
|
102
|
35,36
|
122
|
34,45
|
142
|
33,56
|
3
|
32,98
|
23
|
34,36
|
43
|
34,61
|
63
|
33,51
|
83
|
34,5
|
103
|
34,21
|
123
|
32,77
|
143
|
34,71
|
4
|
33,51
|
24
|
33,44
|
44
|
36,56
|
64
|
34,87
|
84
|
34,16
|
104
|
34,86
|
124
|
31,6
|
144
|
32,73
|
5
|
33,49
|
25
|
35
|
45
|
33,15
|
65
|
32,74
|
85
|
36,09
|
105
|
34,11
|
125
|
33,57
|
145
|
32,44
|
6
|
33,62
|
26
|
35,25
|
46
|
33,22
|
66
|
33,89
|
86
|
33,66
|
106
|
33,9
|
126
|
34,12
|
146
|
34,87
|
7
|
34,73
|
27
|
35,47
|
47
|
34,52
|
67
|
34,59
|
87
|
31,32
|
107
|
35,89
|
127
|
34,48
|
147
|
36,34
|
8
|
34,61
|
28
|
35,29
|
48
|
34,55
|
68
|
34,11
|
88
|
34,94
|
108
|
36,6
|
128
|
32,67
|
148
|
33,3
|
9
|
34,99
|
29
|
33,06
|
49
|
33,58
|
69
|
34,47
|
89
|
32,24
|
109
|
34,17
|
129
|
34,94
|
149
|
34,62
|
10
|
34,28
|
30
|
33,9
|
50
|
33,63
|
70
|
31,4
|
90
|
33,99
|
110
|
35,84
|
130
|
33,68
|
150
|
32,24
|
11
|
35,3
|
31
|
32,81
|
51
|
33,93
|
71
|
34,28
|
91
|
33,8
|
111
|
33,86
|
131
|
33,1
|
151
|
0
|
12
|
33,66
|
32
|
35,13
|
52
|
34,65
|
72
|
33,5
|
92
|
33,02
|
112
|
34,47
|
132
|
34,49
|
152
|
0
|
13
|
33,61
|
33
|
34,17
|
53
|
33,69
|
73
|
33,31
|
93
|
34,2
|
113
|
34,45
|
133
|
34,31
|
153
|
0
|
14
|
34,86
|
34
|
33,51
|
54
|
32,98
|
74
|
34,25
|
94
|
33,73
|
114
|
34,71
|
134
|
34,08
|
154
|
0
|
15
|
32,73
|
35
|
33,17
|
55
|
33,68
|
75
|
33,99
|
95
|
36,76
|
115
|
33,14
|
135
|
32,73
|
155
|
0
|
16
|
34,16
|
36
|
33,55
|
56
|
32,37
|
76
|
35,45
|
96
|
33,77
|
116
|
35,19
|
136
|
32,2
|
156
|
0
|
17
|
35,57
|
37
|
32,93
|
57
|
34,42
|
77
|
34,99
|
97
|
33,28
|
117
|
32,37
|
137
|
33,06
|
157
|
0
|
18
|
33,93
|
38
|
34,07
|
58
|
32,12
|
78
|
35,47
|
98
|
34,19
|
118
|
33
|
138
|
33,92
|
158
|
0
|
19
|
33,65
|
39
|
33,88
|
59
|
33,96
|
79
|
34,3
|
99
|
34,08
|
119
|
33,63
|
139
|
33,85
|
159
|
0
|
20
|
34,18
|
40
|
33,15
|
60
|
34,52
|
80
|
33,9
|
100
|
34,57
|
120
|
34,62
|
140
|
33,43
|
160
|
0
|
1.3 Сортировка
Составляем вариационный ряд, то есть запишем элементы выборки в порядке возрастания:
x(1 )< x(2) < … < x(n).
|
|
x(1)= A =
|
31,32
|
|
x(n)= B =
|
36,76
|
|
Выборочное среднее =
|
34,0082
|
|
На следующей диаграмме дано визуальное представление ранжированной выборки:
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь символами: ◊ обозначены элементы выборки.
|
|
|
|
|
|
|
Для проведения группировки выборки выберем число k. Разобьем отрезок [x(1), x(n)] на k равных частей. Число элементов выборки, попавших в каждый элемент разбиения, называется частотой ni.
n = 150; k = 18; x(1)= A =31,32; x(n)=B = 36,76 . Шаг разбиения h = 0,3022, размах выборки B–A = 5,44.
Р
езультат группирования представлен ниже в таблице.
Г
истограмма частот и график приведенной плотности нормального распределения:
Для данной группированной выборки мы получаем:
выборочное математическое ожидание =34,004;
выборочную дисперсию s2 = 1,0527;
выборочное среднеквадратичное отклонение s = 1,026.
На графике изображена приведенная функция плотности нормального распределения, отличающаяся от истинной функции в nh раз.
В
ыборочные начальные и центральные моменты:
Д
оверительные интервалы для математического ожидания и дисперсии:
1.5 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию хи-квадрат
В

ыполняем новую группировку выборки. При новой группировке стремимся к тому, чтобы во все интервалы попало примерно равное число элементов выборки, но не менее пяти. На рисунке вертикальные отметки указывают границы выбранных интервалов.
В
ычислим r–1 значений функции Ф0(uj) на правых концах интервалов. Значение Ф0(ur)=Ф0(+∞) полагаем равным 0,5.
Разности между наблюдаемым njи ожидаемым значениями npj(nj– число точек попавших в j-й интервал, pj– вероятность того, что значения
с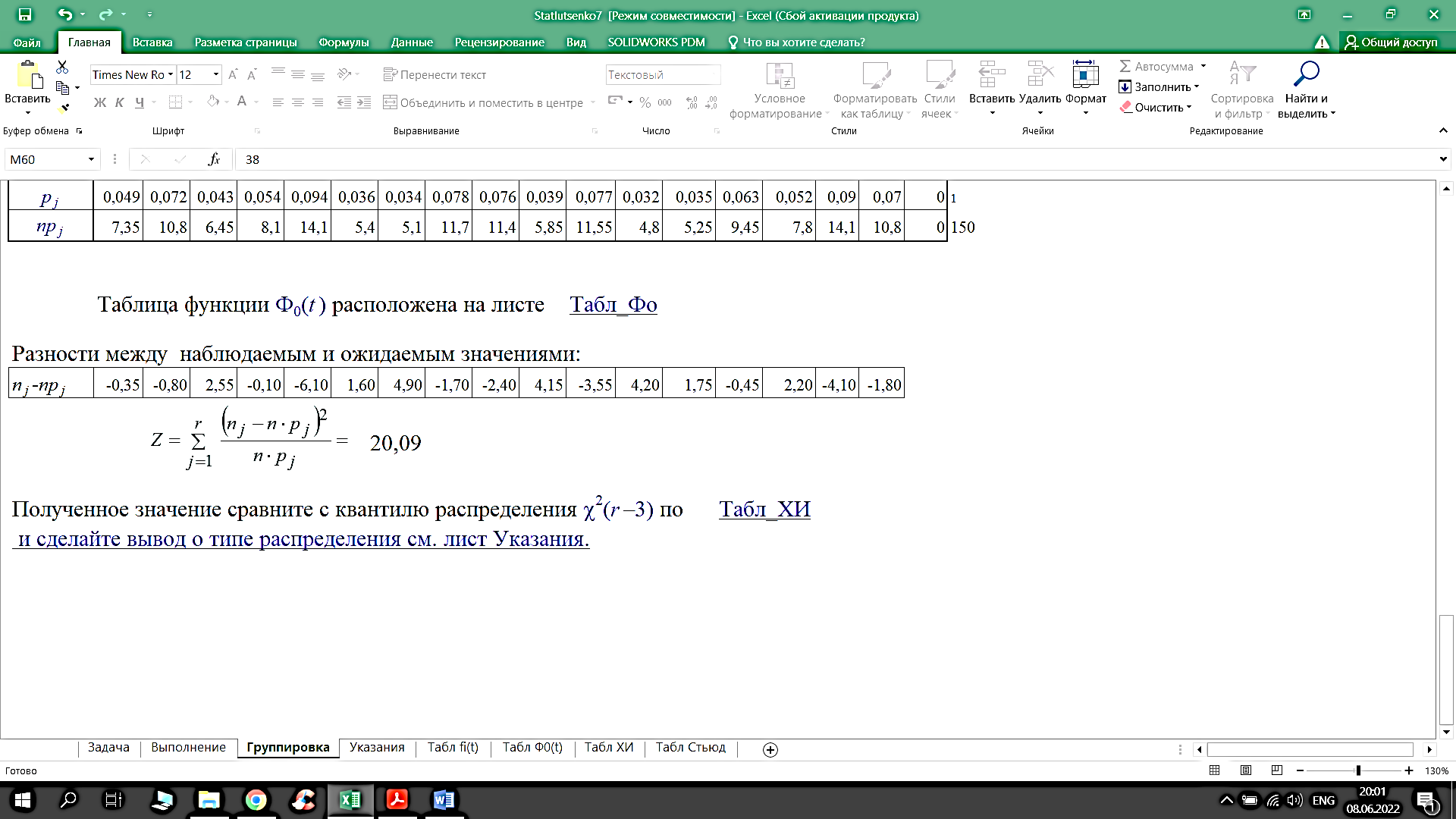
лучайной величины N(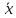 , s) попадут в j-й интервал): , s) попадут в j-й интервал):
Полученное значение сравниваем с квантилем распределения  (r–3). Соответствующее значение для доверительной вероятности (r–3). Соответствующее значение для доверительной вероятности  = 0,95 равно = 0,95 равно  (17–3) = (17–3) =  (14) = 23,68. (14) = 23,68.
1.6 Математические выводы
1. Для выборки объема n=150 найдены значения выборочных начальных и центральных моментов (см. выше).
2. Найдены точечные оценки математического ожидания MX = a, дисперсии DX =  , среднеквадратичного отклонения , среднеквадратичного отклонения 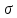 генеральной совокупности X (см. выше). генеральной совокупности X (см. выше).
3. Построены доверительные интервалы для математического ожидания a и дисперсии  для различных значений доверительной вероятности для различных значений доверительной вероятности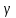 = 0,9; 0,95; 0,99 (см. таблицу) = 0,9; 0,95; 0,99 (см. таблицу)
4. Нет основания отвергнуть гипотезу о нормальности распределения генеральной совокупности X, так как:
– гистограмма частот и график плотности нормального распределения "близки" друг к другу;
– выборочные асимметрия и эксцесс имеют значения "близкие" к нулю;
– по критерию Пирсона (хи-квадрат) критическое значение 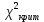 = =  = 23,68 > = 23,68 > 
|
 Скачать 4 Mb.
Скачать 4 Mb.








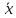 , s) попадут в j-й интервал):
, s) попадут в j-й интервал): (r–3). Соответствующее значение для доверительной вероятности
(r–3). Соответствующее значение для доверительной вероятности  = 0,95 равно
= 0,95 равно  (17–3) =
(17–3) =  (14) = 23,68.
(14) = 23,68. , среднеквадратичного отклонения
, среднеквадратичного отклонения 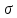 генеральной совокупности X (см. выше).
генеральной совокупности X (см. выше).  для различных значений доверительной вероятности
для различных значений доверительной вероятности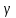 = 0,9; 0,95; 0,99 (см. таблицу)
= 0,9; 0,95; 0,99 (см. таблицу) 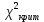 =
=  = 23,68 >
= 23,68 > 

