Лаб_Адиабатический процесс(бригада2). Лабораторная работа 1 адиабатический процесс студент группы твз06110 Ф. И. О. Дьяконов А. Г
 Скачать 158.54 Kb. Скачать 158.54 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 4.1 АДИАБАТИЧЕСКИЙ ПРОЦЕСС Выполнил: студент группы: ТВЗ-06110 Ф.И.О. Дьяконов А.Г. Дата выполнения: 23.01.2021 г. Дата сдачи: 23.01.2021 г. ЛАБОРАТОРНАЯ РАБОТА № 4_1 АДИАБАТИЧЕСКИЙ ПРОЦЕССЦЕЛЬ РАБОТЫ: Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе. Экспериментальное подтверждение закономерностей адиабатического процесса. Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели. КРАТКАЯ ТЕОРИЯ: СОСТОЯНИЕ системы имеет фиксированные значения макроскопических параметров, описывающих систему в целом. Параметры, характеризующие систему в целом, называются ПАРАМЕТРАМИ СОСТОЯНИЯ. Примерами являются температура, давление, объем и т.д. РАВНОВЕСНЫМ называется такое состояние системы, при котором все параметры системы имеют определенные значения, остающееся неизменными сколь угодно долго при неизменных внешних условиях. ОБРАТИМЫМ называется процесс, при реализации которого в обратном направлении система проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Равновесные процессы всегда обратимы. КРУГОВЫМ процессом (ЦИКЛОМ) называется процесс, при котором система после ряда изменений возвращается в исходное состояние. УРАВНЕНИЕ СОСТОЯНИЯ идеального газа (уравнение Менделеева-Клапейрона) 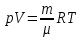 . .ТЕПЛОЕМКОСТЬ тела численно равна отношению количества тепла d’Q, сообщенного телу, к изменению температуры тела dT, которое при этом произошло: СТЕЛА = 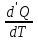 . .УДЕЛЬНОЙ теплоемкостью вещества называется отношение теплоемкости к массе тела. Если тело нем меняет свой объем, то оно не совершает работы, поэтому при постоянном объеме тела переданное телу тепло dQ’ идет на изменение его внутренней энергии dU. ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ОБЪЕМЕ СV = 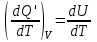 . .ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ идеального газа, молекулы которого имеют i степеней свободы CP = 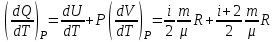 (1). (1).ОТНОШЕНИЕ 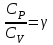 является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты. является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.Формула 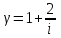 (2) устанавливает связь отношения теплоемкостей с числом степеней свободы молекулы газа i . (2) устанавливает связь отношения теплоемкостей с числом степеней свободы молекулы газа i .ЧИСЛО (количество) СТЕПЕНЕЙ СВОБОДЫ есть минимальное количество независимых координат, необходимых для однозначного описания положения молекулы в пространстве ИЛИ минимальное количество независимых движений, суперпозиция которых дает любое движение молекулы. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ всегда дает 3 степени свободы. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2 степени свободы для линейной молекулы и 3 степени свободы, если атомы в молекуле не расположены на одной линии. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2nКОЛ степеней свободы, где nКОЛ – количество независимых колебаний атомов в молекуле (у двухатомной молекулы nКОЛ = 1). АДИАБАТИЧЕСКИМ называется процесс, происходящий без теплообмена с внешней средой (d’Q = 0). Уравнение адиабаты PV = const (3). Принято также выделять ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и ИЗОХОРИЧЕСКИЙ процессы. Экспериментальная часть: Запустим виртуальную лабораторную установку рис.1. «Адиабатический процесс». Выполним на ней необходимые нам измерения и запишем данные измерений и вычислений в таблицу 1 и 2. 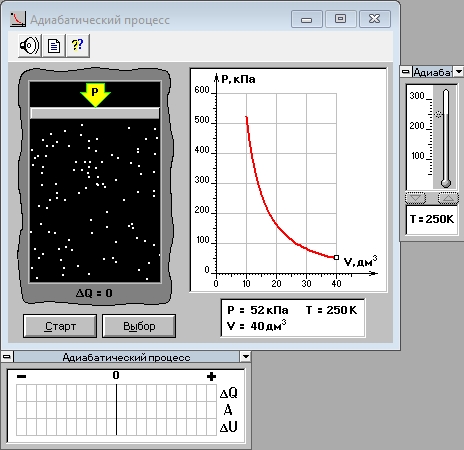 Рис.1. Адиабатический процесс Таблица 1. Измерения и вычисления. 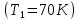
Таблица 2. Измерения и вычисления. 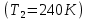
Построим на одном графике зависимости логарифма давления от логарифма объема для обеих адиабат, указав их начальные температуры 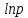 от от 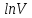 : :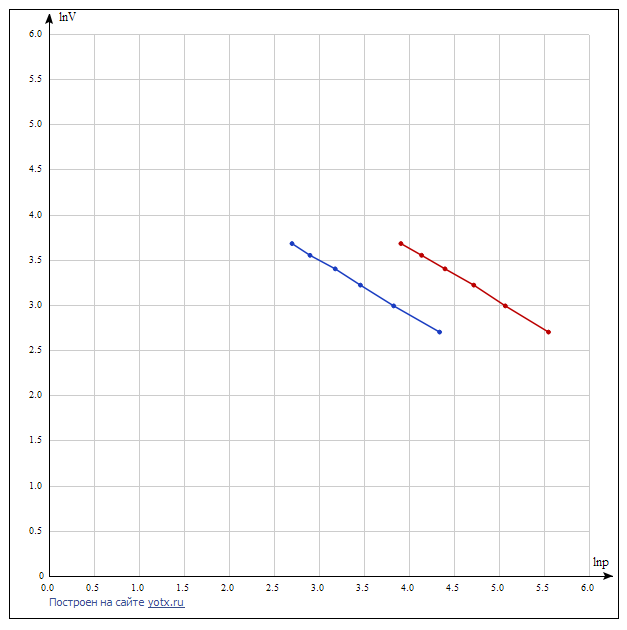 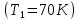 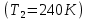 Для каждой адиабаты определим по графику экспериментальное значение показателя по формуле: 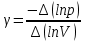 Вычислим значение показателя 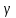 для первой адиабаты для первой адиабаты 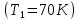 : :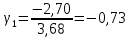 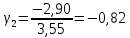 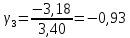 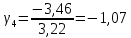 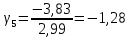 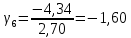 Вычислим значение показателя 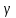 для второй адиабаты для второй адиабаты 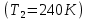 : :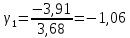 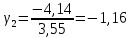 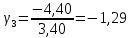 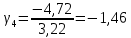 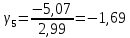 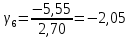 Рассчитаем среднее значение показателя 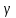 : :для первой адиабаты 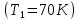 : :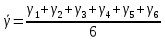 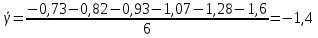 для второй адиабаты 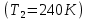 : :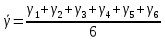 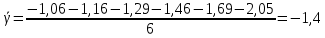 Абсолютная погрешность 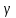 : :для первой адиабаты 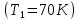 : :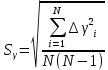 где где 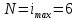 - число опытов, - число опытов,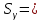 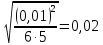 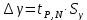 , где , где 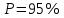 - доверительная вероятность, - доверительная вероятность, 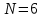 , , 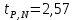 , ,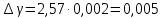 , , Относительная погрешность 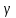 : : 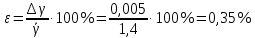 для второй адиабаты 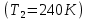 : :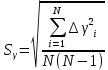 где где 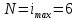 - число опытов, - число опытов,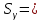 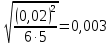 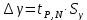 , где , где 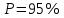 - доверительная вероятность, - доверительная вероятность, 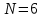 , , 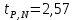 , , , , Относительная погрешность 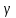 : : 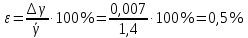 По среднему значению 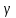 определим число степеней свободы молекулы газа, исследуемого в данной модели: определим число степеней свободы молекулы газа, исследуемого в данной модели: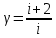 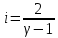 для первой адиабаты 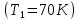 : :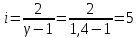 для второй адиабаты 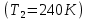 : :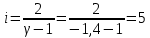 Экспериментально подтвердили число степеней свободы для для двухатомного газа 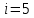 Вывод: познакомились с компьютерной моделью, описывающей адиабатический процесс в идеальном газе. Экспериментально подтверждение закономерности адиабатического процесса. Экспериментально определили показатели адиабаты, количество степеней свободы и структуры молекул газа в данной модели. Вопросы и задания для самоконтроля Дайте определение равновесного состояния системы. ОТВЕТ: Равновесными называют процессы, представляющие собой непрерывную последовательность равновесных состояний системы (равновесное состояние характеризуется, в частности, тем, что все части системы имеют одинаковую температуру и одинаковое давление); Какой процесс называется обратимым? ОТВЕТ: Обратимый процесс считается в физике процессом, который возможен для проведения в обратном направлении таким образом, что система будет подвержена прохождению тех же состояний, но в обратных направлениях. Для какого физического газа можно применить модель «идеальный газ»? ОТВЕТ: Идеальным газом называют модель, состоящую из очень большого количества частиц, которые вне контакта не взаимодействуют друг с другом (движутся свободно), а при контакте сталкиваются абсолютно упруго. Реальные газы ведут себя подобно идеальным при достаточно больших разрежениях, когда расстояния между молекулами во много раз больше их размеров. Опыт показывает, что при давлениях, близких к атмосферному, и температурах, близких к комнатной, многие газы (азот, кислород, водород, пары воды и т.д.) можно считать идеальными. Энергией взаимодействия молекул между собой здесь можно пренебречь потому, что в этих условиях лишь небольшая доля молекул находится в каждый момент времени в состоянии соударения. Что такое показатель адиабаты? ОТВЕТ: Показатель адиабаты по-другому называют коэффициентом Пуассона или фактором изоэнтропийного расширения. Для обозначения этой величины используют греческую букву γ (гамма) или κ (каппа). Показатель адиабаты рассчитывают из отношения между изобарной теплоемкостью газообразного вещества и его изохорной теплоемкостью. 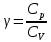 Напишите формулу связи показателя адиабаты с числом степеней свободы молекулы идеального газа. ОТВЕТ: Формула, устанавливающая связь показателя адиабаты γ с числом степеней свободы молекулы газа i: 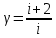 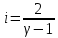 |