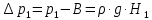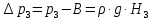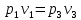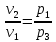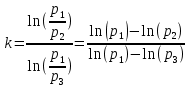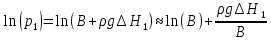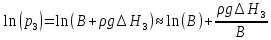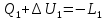Лабораторная работа №2. Лабораторная работа 2 Определение показателя адиабаты воздуха Кожевников М. В. Студент группы пс002
 Скачать 117.54 Kb. Скачать 117.54 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «Петербургский государственный университет путей сообщения Императора Александра I» (ФГБОУ ВО ПГУПС) Кафедра «Электротехника и теплоэнергетика» Лабораторная работа № 2 Определение показателя адиабаты воздуха Выполнил: Кожевников М.В. Студент группы ПС-002 Проверил(а): Митрофанова И. В. Рыжова Е. Л. Санкт – Петербург 2022г. 1. Цель работы: экспериментальное определение показателя адиабаты 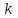 при адиабатном процессе истечения воздуха и сравнение опытных данных с табличными. при адиабатном процессе истечения воздуха и сравнение опытных данных с табличными.Основные теоретические положения Адиабатным называется процесс изменения состояния газа, протекающий без теплообмена с внешней средой ( 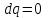 и и 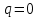 ). С некоторой погрешностью такой процесс можно осуществить при тепловой изоляции системы от внешней среды или при большой скорости протекания процесса, когда теплообмен с внешней средой практически отсутствует. ). С некоторой погрешностью такой процесс можно осуществить при тепловой изоляции системы от внешней среды или при большой скорости протекания процесса, когда теплообмен с внешней средой практически отсутствует.Определить опытным путем показатель адиабаты (коэффициент Пуассона) можно при реализации адиабатного процесса быстрого расширения предварительно сжатого газа в жёсткой ёмкости при открытии клапана, соединяющего ёмкость с атмосферой (рис. 1, процесс 1-2) с измерением его начальных и конечных параметров. В соответствии с уравнением обратимого адиабатного процесса: 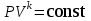 , (1) , (1)где 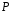 –давление газа, Па; –давление газа, Па; 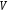 – удельный объем газа, м³/кг; – удельный объем газа, м³/кг;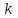 – показатель адиабаты, величина которого зависит от атомности газа и равна отношению изобарной и изохорной теплоемкостей: – показатель адиабаты, величина которого зависит от атомности газа и равна отношению изобарной и изохорной теплоемкостей: 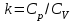 . (2) . (2)При известных параметрах ( 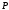 и и 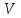 )для двух крайних точек адиабатного процесса уравнение (1) можно записать в виде )для двух крайних точек адиабатного процесса уравнение (1) можно записать в виде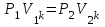 (3) (3)или 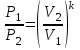 . (4) . (4)Прологарифмировав выражение (1), получим формулу для вычислений коэффициента Пуассона (показателя адиабаты): 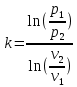 . (5) . (5)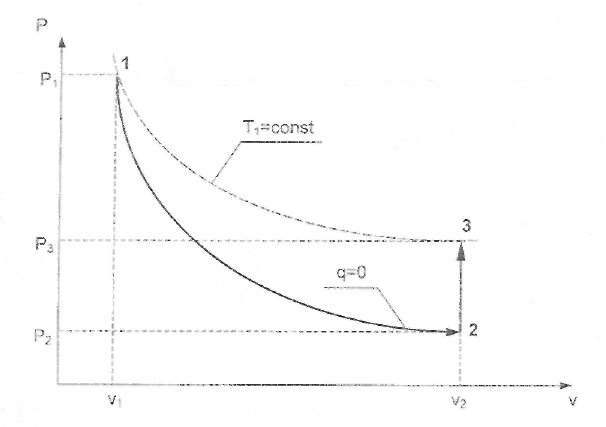 Рис. 1. Адиабатно - изохорный процесс, происходящий в замкнутом объеме при выпуске воздуха из баллона. В соответствии с (5) для определения коэффициента Пуассона необходимо знать два параметра газа в двух точках этого процесса. Однако существует более простой способ экспериментального определения коэффициента Пуассона для газов. При этом достаточно замерить избыточное давление газа в баллоне в нескольких состояниях (рис. 1): первое – ΔН1 при заполненном баллоне и температуре внешней среды (точка 1), второе - ΔНз после изохорного нагрева оставшегося в баллоне газа до температуры внешней среды (точка 3). В установке в первоначальном состоянии (точка 1) газ в баллоне имеет давление больше атмосферного P1>B и температуру, равную температуре внешней среды T1=Toc. При открытии выпускного крана происходит адиабатное расширение газа в баллоне (процесс 1-2) до атмосферного давления Р2=В. В результате реализации адиабатного расширения газа его температура уменьшается до температуры, меньшей, чем у внешней среды Т2<ТОС. При закрытии выпускного крана в баллоне происходит изохорный процесс 2-3 нагрева газа до температуры, равной внешней среды Тз=Т0С. Необходимо обратить внимание на то, что в данном процессе 1-2-3 речь идет только о той части газа, которая находится в баллоне. Поскольку объем баллона не изменяется, то изменение удельного объема газа в баллоне при адиабатном расширении 1-2 происходит за счет выпуска части газа из баллона во внешнюю среду. Реализация такого процесса позволяет определить коэффициент Пуассона на основании выражения (5) и двух избыточных давлений газа в баллоне:
где: 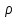 - плотность жидкости в манометре, кг/м3;g - ускорение свободного падения; - плотность жидкости в манометре, кг/м3;g - ускорение свободного падения;
H1 и Н3 - разница высот столбов жидкости в манометре в начале и конце опыта (точки 1 и 3). Выражение (5) можно преобразовать следующим образом. Для условного изотермического процесса 1-3 справедливо равентсво:
Следовательно, поскольку v2 = v3, справедливо соотношение:
Заменив отношение объемов в (5) на отношение давлений в соответствии с (9) получим равенство:
В свою очередь, Р2= В, а логарифмы давлений P1 и Р3 можно разложить в ряд Тейлора, ограничиваясь первыми членами. Это допустимо, поскольку величины избыточных давлений ρgΔН1 и ρgΔН3 малы по сравнению с атмосферным давлением В:
Подставив (11) и (12) в соотношение (10), получим расчетную формулу коэффициента Пуассона для данной экспериментальной установки: 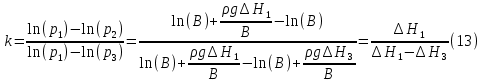 Таким образом, расчет коэффициента Пуассона выполняется на основании (13). Отметим, что процессы, происходящие в ёмкости, не являются равновесными и их нельзя отобразить графически. Приведённые графики являются некоторым приближение к реальным процессам, происходящим в опыте. Применение предложенной методики связано с некоторыми методическими и техническими трудностями, а именно: - в процессе адиабатного расширения участвует только часть воздуха, находящегося в ёмкости в то же время другая часть участвует в неравновесном процессе истечения через проходное сечение клапана во время его открытия; - не возможно осуществить «чистый» адиабатный процесс в предложенной методике, так как для сброса давления в ёмкости необходимо некоторое время τ(пусть даже очень малое). В течение этого времени произойдёт частичный теплообмен той части воздуха которая контактирует со стенками ёмкости вследствие уменьшения его внутренней энергии, то есть воздух в ёмкости получит некоторое количество теплоты от стенок ёмкости Q1.
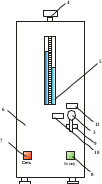
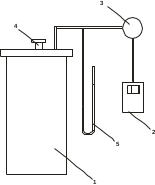
- после закрытия клапана в процессе изохорного нагрева участвует только оставшаяся часть воздуха в ёмкости, которая получит от стенок тепло Q2 = ∆U2 - с другой стороны физически трудно определить момент закрытия клапана в конце неравновесного процесса выравнивания давления в ёмкости с атмосферой.При открытии клапана происходят затухающие колебания жидкости, находящейся в U- манометре, что затрудняет зафиксировать момент закрытия клапана; Но с учётом указанных методических и технических погрешностей этот метод может быть применён для изучения указанных процессов. Полезные выводы: 1.Для уменьшения части воздуха, участвующей в неравновесном процессе истечения через проходное сечение клапана во время его открытия, перепад давления ∆Н1 должен быть не более 15 … 20 см. 2. Стенки ёмкости должны быть жёсткими. 3. Ёмкость должна быть изготовлена из материала с малой величиной теплопроводности. 4. Проходное сечение клапана сброса должно быть максимальным. 5. Момент времени закрытия клапана должен соответствовать моменту времени выравнивания столбов жидкости в U – манометре первой четверти первого колебания. 3. Описание экспериментальной установки: Общий вид лицевой панели лабораторной установки представлен на рис. 2. Принципиальная схема лабораторной установки приведена на рис. 3. В стеклянный баллон (1), соединенный с компрессором (2), через впускной кран (3) накачивается воздух. Клапан сброса воздуха (4), находящийся на верхней крышке установки позволяет резко уменьшить давление в баллоне практически без теплообмена с окружающей средой. Кран (3) имеет следующие положения: «ОТКРЫТ» - положение ручки крана на данной метке открывает линию к компрессору (2); «ЗАКРЫТ» - положение ручки крана на данной отметке перекрывает баллон (1); «РЕГУЛИРОВАНИЕ УРОВНЯ» - положение ручки на данной отметке позволяет отрегулировать уровень воды в U-образном манометре после заполнения баллона воздухом. Установка работает следующим образом. В баллон компрессором (2) закачивается воздух до определенного избыточного давления (разность уровней в коленах U- манометра должна составлять: Dh = (20 … 25) см.). В каждой серии опытов эта разность должна быть одинаковой (регулируется краном (3)). После выравнивания температур воздуха в баллоне и окружающей среды, осуществляется быстрый сброс давления через выпускное отверстие с клапаном. При этих условиях процесс с достаточной точностью можно считать адиабатическим. После того, как клапан сброса закрылся, осуществляется изохорный процесс теплообмена с окружающей средой. Температура воздуха в баллоне приближается к температуре окружающей среды.
3. Порядок выполнения работы: 1. Включить установку тумблером (7) «СЕТЬ», Повернуть ручку крана 3 в положение «ОТКРЫТ»(9). Включить тумблером (8) компрессор. Установить разность уровней воды в манометре составляла 20 … 25 мм. Поле этого закрыть напускной клапан поворотом ручки крана (3) в положение «ЗАКРЫТ» (10). 2. Подождать 2 … 4 минуты до тех пор, пока температура воздуха в баллоне не станет равна температуре окружающей среды. 3. Произвести дополнительную регулировку разности уровней в манометре, стремясь к тому, чтобы в каждом опыте эта разность была постоянной. При этом ручка крана (3) плавно переводится в положение «РЕГУЛИРОВКА УРОВНЯ»(11) и обратно. 4. По нижнему уровню мениска определить уровни H1 и H2 в коленах манометра. Записать эти значения а также их разность в таблицу 1. 5. Резко (Но не сильно!) нажать и отпустить выпускной клапан (4) (баллон соединяется с атмосферой). 6. Через 3 … 4 минуты, после того как уровни воды в манометре стабилизируются, определить значения уровней h1 и h2 и занести результаты в таблицу. 7. Повторить пункты 1 … 6 несколько раз. Следить за тем, чтобы начальная разность уровней в манометре была постоянной (пункт 3). 4. Таблица результатов эксперимента Таблица 1
5. Расчёт основных величин производится по формулам: 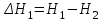 ; ; 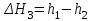 ; ; 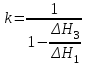 ; ;
По выражению (13) подсчитывают величину показателя адиабаты kдля каждого опыта. Затем вычисляют среднее значение kср (kоп). Погрешность определения показателя адиабаты, %: 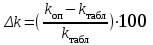 . .Для оценки корректности проведенного опыта необходимо сравнить полученное в опыте значение коэффициента Пуассона со значением коэффициента Пуассона для идеального воздуха, считая его двухатомным газом k = (i + 2) / i, где: i - число степеней свободы молекулы данного газа. 7. Заключение (сформулировать выводы на основании произведенных измерений экспериментальным путем значения показателя адиабаты k = cр / cv для воздуха, сравнивая с табличной величиной): Входе эксперимента погрешность составила ,% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||