COM объекты. ЛБ 1_Com. Лабораторная работа 1 часть 1 взаимодействие с унаследованным программным кодом 1 реализация внутреннего сервера com в delphi 2

• Название: Лабораторная работа 1 часть 1 взаимодействие с унаследованным программным кодом 1 реализация внутреннего сервера com в delphi 2
• Анкор: COM объекты
• Дата: 28.05.2022
• Размер: 0.79 Mb.
• Имя файла: ЛБ 1_Com.doc
• Тип: Лабораторная работа; #554589
• страница: 13 из 13

ШИФРОВАНИЕ МЕТОДОМ ГАММИРОВАНИЯ

Под гаммированием понимают процесс наложения по оп­ределенному закону гаммы шифра на открытые данные. Гамма шифра - это псевдослучайная последовательность, выработанная по заданному алгоритму для зашифрования открытых данных и расшифрования зашифрованных данных.

Процесс зашифрования заключается в генерации гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым образом, например с использованием операции сложения по модулю 2.

Следует отметить, что перед зашифрованием открытые данные разбивают на блоки Т₀⁽ⁱ⁾ одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности блоков Г_ш⁽ⁱ⁾ аналогичной длины.

Уравнение зашифрования можно записать в виде

Т_ш⁽ⁱ⁾ = Г_ш⁽ⁱ⁾  T₀⁽ⁱ⁾ , i = 1 ... М

где Т_ш⁽ⁱ⁾ - i-й блок шифртекста; Г_ш⁽ⁱ⁾ - i-й блок гаммы шифра; Т₀⁽ⁱ⁾ -
i-й блок открытого текста; М - количество блоков открытого текста.

Процесс расшифрования сводится к повторной генерации гаммы шифра и наложению этой гаммы на зашифрованные дан­ные. Уравнение расшифрования имеет вид

Т₀⁽ⁱ⁾ = Г_ш⁽ⁱ⁾  T_ш⁽ⁱ⁾

Получаемый этим методом шифртекст достаточно труден для раскрытия, поскольку теперь ключ является переменным. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого блока. Если период гаммы превышает длину всего шифруемого текста и злоумышленнику неизвестна никакая часть исходного текста, то такой шифр можно раскрыть только прямым перебором всех вариантов ключа. В этом случае криптостойкость шифра определяется длиной ключа.

Методы генерации псевдослучайных последовательностей чисел

При шифровании методом гаммирования в качестве ключа используется случайная строка битов, которая объединяется с открытым текстом, также представленным в двоичном виде (на­пример, А = 00000, В = 00001, С = 00010 и т.д.), с помощью побитового сложения по модулю 2, и в результате получается шифро­ванный текст. Генерирование непредсказуемых двоичных после­довательностей большой длины является одной из важных про­блем классической криптографии. Для решения этой проблемы широко используются генераторы двоичных псевдослучайных по­следовательностей.

Генерируемые псевдослучайные ряды чисел часто назы­вают гаммой шифра или просто гаммой (по названию буквы  греческого алфавита, часто используемой в математических фор­мулах для обозначения случайных величин).

Обычно для генерации последовательности псевдослу­чайных чисел применяют компьютерные программы, которые, хотя и называются генераторами случайных чисел, на самом деле вы­дают детерминированные числовые последовательности, которые по своим свойствам очень похожи на случайные.

К криптографически стойкому генератору псевдослучайной последовательности чисел (гаммы шифра) предъявляются три основных требования:

1. 
   период гаммы должен быть достаточно большим для шифро­вания сообщений различной длины;
   
2. 
   гамма должна быть практически непредсказуемой, что означает невозможность предсказать следующий бит гаммы, даже если известны тип генератора и предшествующий кусок гаммы;
   
3. 
   генерирование гаммы не должно вызывать больших техниче­ских сложностей.
   

Длина периода гаммы является самой важной характери­стикой генератора псевдослучайных чисел. По окончании периода числа начнут повторяться, и их можно будет предсказать. Требуе­мая длина периода гаммы определяется степенью закрытости данных. Чем длиннее ключ, тем труднее его подобрать. Длина периода гаммы зависит от выбранного алгоритма получения псевдослучайных чисел.

Второе требование связано со следующей проблемой: как можно достоверно убедиться, что псевдослучайная гамма конкретного генератора является действительно непредсказуемой? Пока не существуют такие универсальные и практически проверяемые критерии и методики. Чтобы гамма считалась непредсказуемой, т.е. истинно случайной, необходимо, чтобы ее период был очень большим, а различные комбинации битов определенной длины были равномерно распределены по всей ее длине.

Третье требование обусловливает возможность практической реализации генератора программным или аппаратным путем с обеспечением необходимого быстродействия.

Один из первых способов генерации псевдослучайных чи­сел на ЭВМ предложил в 1946 г. Джон фон Нейман. Суть этого способа состоит в том, что каждое последующее случайное число образуется возведением в квадрат предыдущего числа с отбрасы­ванием цифр младших и старших разрядов. Однако этот способ оказался ненадежным и от него вскоре отказались.

Из известных процедур генерации последовательности псевдослучайных целых чисел наиболее часто применяется так называемый линейный конгруэнтный генератор. Этот генератор вырабатывает последовательность псевдослучайных чисел Y₁, Y₂, ..., Y_i-1, Y_i, ..., используя соотношение

Yi = (a*Y_i-1 + b) mod m,
где Yi - i-e (текущее) число последовательности; Y_i-1 - предыду­щее число последовательности; а, Ь и m - константы; m - модуль;
а - множитель (коэффициент); b - приращение; Y₀ - порождающее
число (исходное значение).

Текущее псевдослучайное число Yi получают из предыду­щего числа Y_i-1 умножением его на коэффициент а, сложением с приращением b и вычислением остатка от деления на модуль m. Данное уравнение генерирует псевдослучайные числа с периодом повторения, который зависит от выбираемых значений параметров а, Ь и m и может достигать значения m. Значение модуля m бе­рется равным 2ⁿ либо равным простому числу, например m=2³¹-1. Приращение b должно быть взаимно простым с m, коэффициент а должен быть нечетным числом.

Конгруэнтные генераторы, работающие по алгоритму, предложенному Национальным бюро стандартов США, использу­ются, в частности, в системах программирования. Эти генераторы имеют длину периода 2²⁴ и обладают хорошими статистическими свойствами. Однако такая длина периода мала для криптографи­ческих применений. Кроме того, доказано, что последовательно­сти, генерируемые конгруэнтными генераторами, не являются криптографически стойкими.

Существует способ генерации последовательностей псев­дослучайных чисел на основе линейных рекуррентных соотноше­ний.

Рассмотрим рекуррентные соотношения и их разностные уравнения:

_k

 h_j *a_i+j=0

^j=0

_k-1

a_i+k=- h_j *a_i+j

^j=0
где h₀0, h_k=1 и каждое h_i принадлежит полю GF(q).

Решением этих уравнений является последовательность элементов а₀,а₁,а₂,... поля GF(q). Соотноше­ние определяет правило вычисления a_k по известным зна­чениям величин a₀,a₁,a₂,...,a_k-1.Затем по известным значениям a₀,a₁,a₂,...,a_k находят a_k+1 и т.д. В результате по начальным зна­чениям a₀,a₁,a₂,...,a_k-1можно построить бесконечную последова­тельность, причем каждый ее последующий член определяется из k предыдущих. Последовательности такого вида легко реализу­ются на компьютере, при этом реализация получается особенно простой, если все h_i и а_i, принимают значения 0 и 1 из поля GF(2).

На рис. показана линейная последовательная пере­ключательная схема, которая может быть использована для вы­числения суммы и, следовательно, для вычисления значе­ния a_k по значениям k предыдущих членов последовательности. Исходные величины a₀,a₁,a₂,...,a_k-1 помещаются в разряды сдви­гового регистра, последовательные сдвиги содержимого которого соответствуют вычислению последовательных символов, при этом выход после i-ro сдвига равен а_i. Данное устройство генератором последовательности чисел, построенным на базе сдвигового регистра с линейной обратной связью.

Решения линейных рекуррентных соотношений, реализуе­мые генератором с регистром сдвига, описываются следующей теоремой. Пусть многочлен

h(X)=  hjX^j,

где X - формальная переменная; hj - коэффициент при X^j, при­нимающий значение 0 или 1; h₀ 0, h_k= 1, и пусть n - наименьшее целое положительное число, для которого многочлен Хⁿ - 1 де­лится на h(X).

К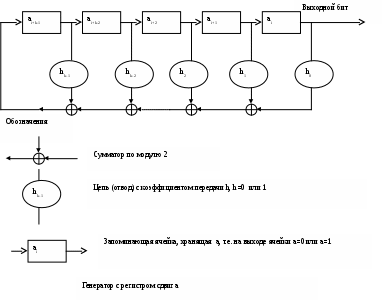
роме того, многочлен g(x)=(Xⁿ-1)/h(X)

Тогда решения рекуррентных соотношений

_k

 h_j *a_i+j=0

^j=0
в виде последовательности элементов а₀,а₁,а_i,...a_n-1 периодичны с периодом n и совокупность, составленная из первых периодов всех возможных решений, рассматриваемых как многочлены по модулю (Хⁿ-1),т.е.

a(X)= а₀*X^n-1+ а₁*X^n-2 + ….+а_n-2*X+ а_n-1.

совпадает с идеалом, порожденным многочленом g (X) в алгебре многочленов по модулю (Хⁿ - 1). Доказательство этой теоремы можно найти в книге Питерсон У, Уэлдон Э. «Коды, исправляющие ошибки».

Заметим, что если при таком определении многочлена а(Х) элементы а₀,а₁,а₂,... вычисляются в порядке возрастания номеров, то коэффициенты многочлена а(Х) вычисляются, начи­ная с коэффициентов при степенях высших порядков. Следует также отметить, что вид многочлена
_k

h(X)= h_j *x^j=0

^j=0

определяет конфигурацию обратных связей (отводов) hj в генераторе со сдвиговым регистром. Другими словами, если у многочлена h(X) коэффициент hj= 1, это означает, что отвод hj в схеме генератора присутствует, если же у многочлена h(X) коэффициент hj = 0, то отвод hj в схеме генератора отсутствует. В [Питерсон У, Уэлдон Э. «Коды, исправляющие ошибки»] показано, что в качестве h(Х) необходимо выбирать неприводимый примитивный многочлен. При таком выборе многочлена h(X) со старшей степенью m генератор обеспечивает выдачу псевдослучайной последовательности двоичных чисел с макси­мально возможным периодом 2^m - 1 .

Рассмотрим в качестве примера трехразрядный сдвиговый регистр с линейной обратной связью, построенный в соответствии с неприводимым примитивным многочленом

h(Х) = X³ + X² + 1,

где коэффициенты h₃=1, h₂ = 1, h₁ = 0, h₀=1.

Пусть ключом является 101. Регистр начинает работать с этого состояния; последовательность состояний регистра приве­дена на рис.

Регистр проходит через все семь ненулевых со­стояний и снова возвращается в свое исходное состояние 101. Это - наиболее длинный период данного регистра с линейной об­ратной связью. Такая последовательность называется последо­вательностью максимальной длины для сдвигового регистра (Maximal Lenght Shift Register Sequence - MLSRS). Питерсон и Уэлдон показали, что при любом целом m существует m-битовая последовательность MLSRS с периодом 2^m - 1. В частно­сти, при m =100 последовательность будет иметь период 2¹⁰⁰ - 1 и не повторится 10¹⁶ лет при передаче ее по линии связи со ско­ростью 1 Мбит/с.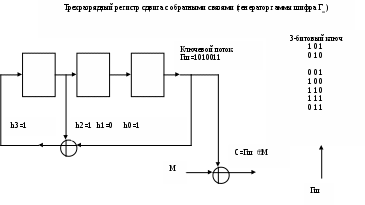


В данном примере выходной последовательностью (гаммой шифра) Г_ш сдвигового регистра с обратной связью является по­следовательность 1010011, которая циклически повторяется. В этой последовательности имеется четыре единицы и три нуля, и их распределение настолько близко к равномерному, насколько это возможно в последовательности, имеющей длину 7. Если рас­смотреть пары последовательных битов, то пары 10 и 01 появ­ляются по два раза, а пары 00 и 11 - один раз, что опять оказы­вается настолько близким к равномерному распределению, насколько это возможно. В случае последовательности максималь­ной длины для m-разрядного регистра это свойство равнораспре­деленности распространяется на тройки, четверки и т.д. битов, вплоть до m-битовых групп. Благодаря такой близости к равно­мерному распределению последовательности максимальной дли­ны часто используются в качестве псевдослучайных последова­тельностей в криптографических системах, которые имитируют работу криптостойкой системы одноразового шифрования.

Хотя такая криптографическая система осуществляет ими­тацию заведомо криптостойкой системы одноразового шифрова­ния, сама она не отличается стойкостью и может быть раскрыта за несколько секунд работы компьютера при условии наличия из­вестного открытого текста [Диффи У. Хеллман М.Э. «Защищенность и имитостойкость. Введение в криптографию»].

Если отводы регистра с обратной связью зафиксированы, то для нахождения начального состояния регистра достаточно знать m битов открытого текста. Чтобы найти m битов ключевого потока, m битов известного открытого текста складывают по мо^: дулю 2 с соответствующими m битами шифртекста. Полученные m битов дают состояние сдвигового регистра с обратной связью в обратном направлении на некоторый момент времени. Затем, мо­делируя работу регистра назад, можно определить его исходное состояние.

Если отводы регистра с обратной связью не фиксированы, а являются частью ключа, то достаточно 2m битов известного от­крытого текста, чтобы сравнительно быстро определить располо­жение отводов регистра и его начальное состояние. Пусть S(i) -вектор-столбец, состоящий из m символов 0 и 1, который опре­деляет состояние регистра в i-й момент времени. Тогда

S(i + 1) = A*S(i) mod 2,

где А — матрица размером m x m, определяющая положение от­водов регистра с обратной связью.

Для трехразрядного регистра

| 1 0 1 |

А = | 1 0 0 |

| 1 0 1 |

Матрица А всегда имеет следующую структуру: в ее пер­вой строке отражена последовательность отводов в регистре, не­посредственно под главной диагональю располагаются единицы, а в остальных позициях располагаются нули.

2m битов известного открытого текста позволяют вычис­лить 2т последовательных битов ключевого потока. Для упрощения обозначений предположим, что это - первые 2 m битов ключевого потока. Следовательно,

• S(1) - первая группа m известных битов ключевого, потока;

• S(2) - следующая группа (начиная с номера 2) из m извест­ных битов ключевого потока;

• S(m+1) - последняя группа из m известных битов ключевой потока.

Далее можно образовать две матрицы размером m x m:

X(1) = [S(1), S(2), ... S(m)]

X(2) = [S(2), S(3), ..., S(m+1)]
которые связаны соотношением X(2) = A*X(1)mod2.

Можно показать, что для любой последовательности мак­симальной длины матрица Х(1) всегда несингулярна, поэтому матрицу А можно вычислить как

А = Х(2)[Х(1)]-¹ mod 2.

Обращение матрицы Х(1) требует (самое большее) поряд­ка m³ операций, поэтому легко выполняется при любом разумном значении m.

Д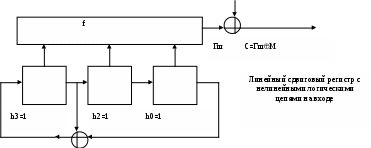
ля криптографии последовательности максимальной длины MLSRS можно сделать более криптостойкими, используя нелинейную логику. В частности, предложен вариант [Диффи У. Хеллман М.Э. «Защищенность и имитостойкость. Введение в криптографию»], в кото­ром в качестве ключевого потока используется нелинейно "фильт­рованное" содержимое сдвигового регистра, а для получения по­следовательности максимальной длины - линейная обратная связь (см. рис.).

Функция f должна выбираться так, чтобы обеспечить хо­роший баланс между нулями и единицами, а фильтрованная по­следовательность имела распределение, близкое к равномерно­му. Необходимо также, чтобы фильтрованная последовательность имела большой период. Если (2^m - 1) является простым числом (как в примере: при m = 3 имеем 2³ - 1 = 7), то фильтрованная последовательность может иметь период (2^m - 1) (при выборе структуры сдвигового регистра в соответствии с неприводимым примитивным многочленом h(Х) степени m).

К таким значениям m относятся, в частности, следующие: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, а полученные таким образом простые числа называются просты­ми числами Мерсенна.

Несмотря на то, что фильтрованную выходную последова­тельность обычно нельзя получить с помощью m-разрядного сдви­гового регистра с линейной обратной связью, ее всегда можно по­лучить с помощью сдвигового регистра большей длины с линей­ной обратной связью [Месси Дж. П. «Введение в современную криптологию»]. Регистр длиной (2^m - 1) всегда позволит это сделать, а иногда пригоден и более короткий регистр.

Еще более привлекательно использование в цепи обрат­ной связи нелинейной логики, однако теория таких схем недоста­точно хорошо освещена (в открытой литературе).