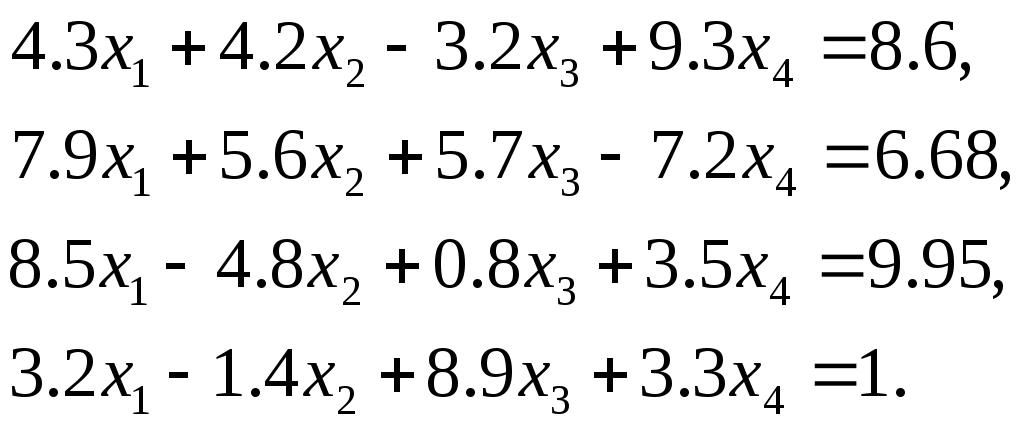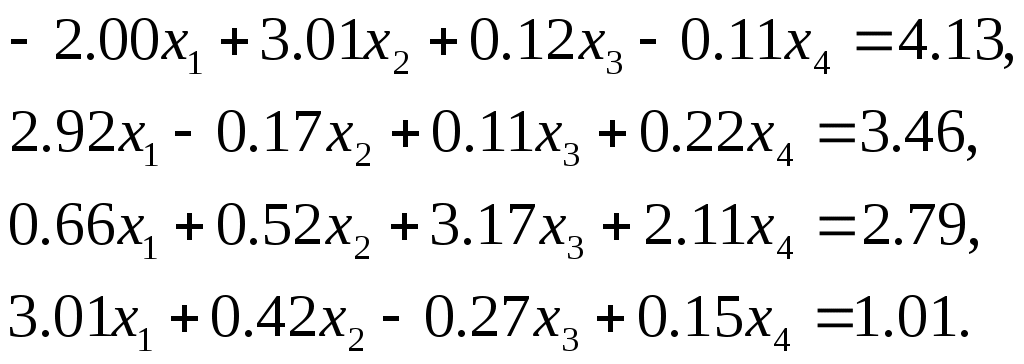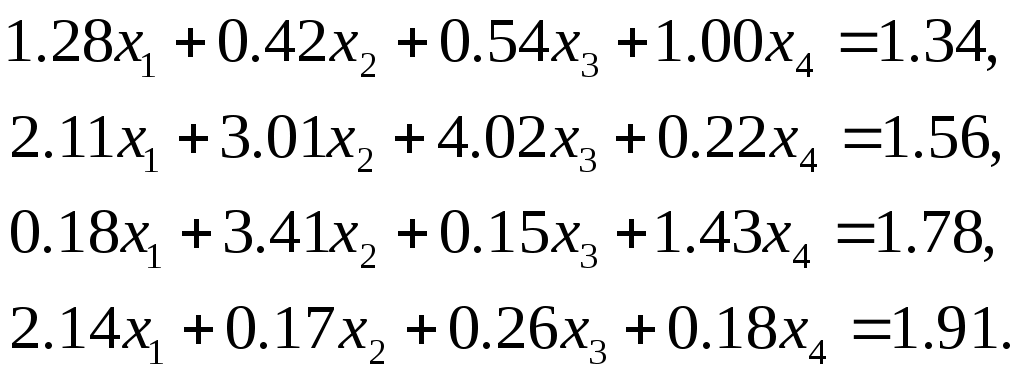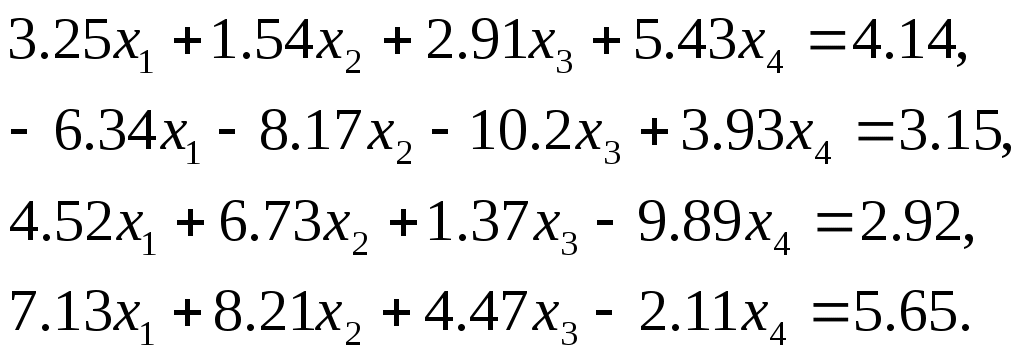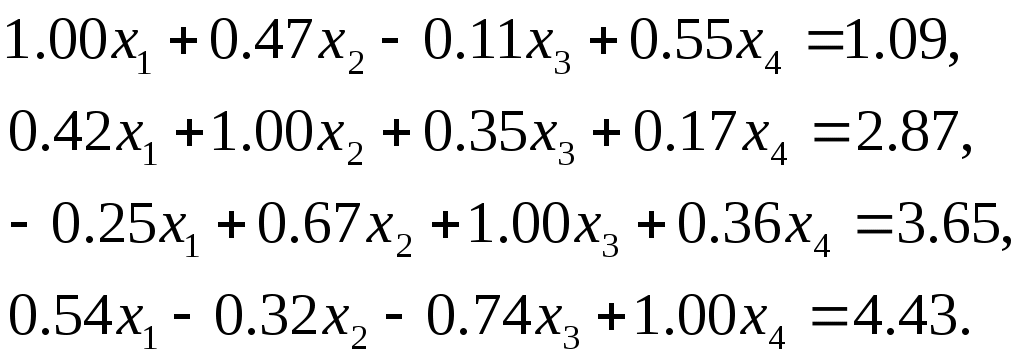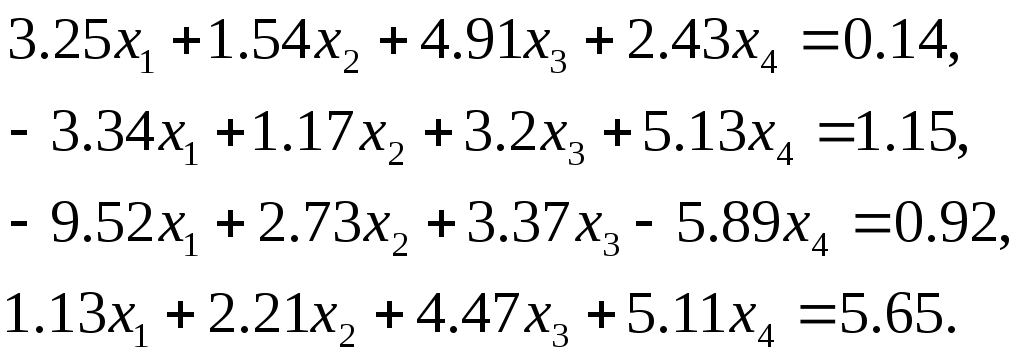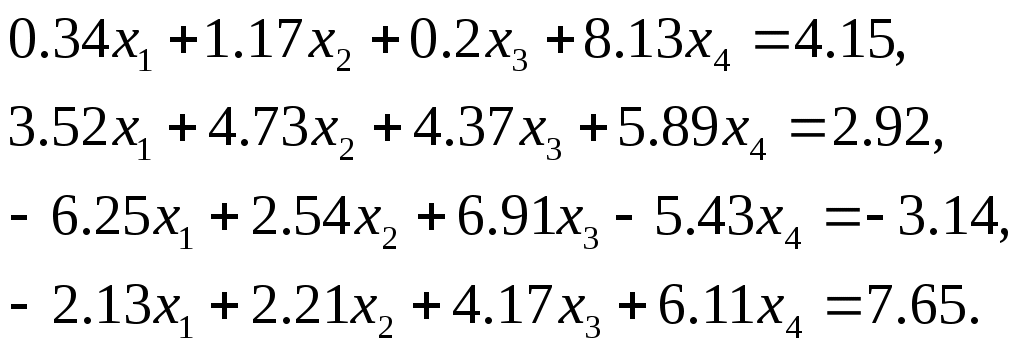Лабораторная работа 1 Численные методы решения систем линейных алгебраических уравнений. Метод Гаусса с выбором главного элемента
 Скачать 89 Kb.
|
|
Лабораторная работа №1 Численные методы решения систем линейных алгебраических уравнений. Метод Гаусса с выбором главного элемента Методы решения систем линейных алгебраических уравнений (СЛАУ) можно разделить на две группы: 1) прямые (точные); 2) итерационные (методы последовательных приближений). С помощью точных методов, проделав конечное число операций, можно получить точные значения неизвестных. При этом предполагается, что коэффициенты и правые части системы известны точно, а все вычисления проводятся без округлений. Примером прямого метода является метод Гаусса. Пусть задана СЛАУ  (1)где A– вещественная квадратная матрица порядка n, а f– заданный и x– искомый векторы. Будем предполагать, что определитель матрицы A отличен от нуля. Тогда для каждого вектора f система (1) имеет единственное решение. Или можно записать систему (1) в развернутом виде 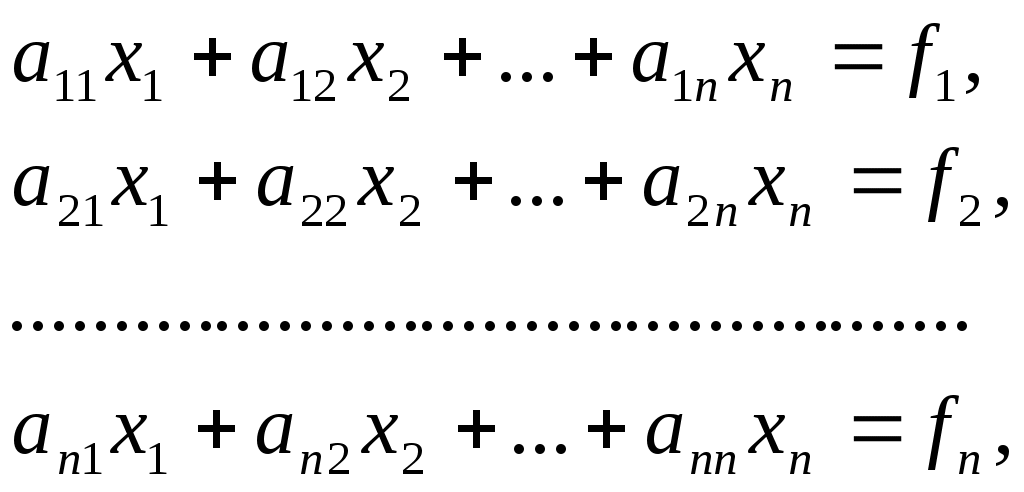 (2)Метод Гаусса решения системы (2) состоит в последовательном исключении неизвестных  из этой системы (курс алгебры). После исключения неизвестных система (2) преобразуется в систему, матрица которой содержит нули всюду ниже главной диагонали. Получение такой системы называется прямой ход метода Гаусса. Обратный ход заключается в нахождении неизвестных из полученной системы.Может оказаться, что система  имеет единственное решение, хотя какой-либо из угловых миноров матрицы A равен нулю. Кроме того, заранее неизвестно, все ли угловые миноры матицы Aотличны от нуля. Избежать указанных трудностей позволяет метод Гаусса с выбором главного элемента. Основная идея состоит в том, чтобы на очередном шаге исключать не следующее по номеру неизвестное, а то неизвестное, коэффициент при котором является наибольшем по модулю. Различают метод Гаусса с выбором главного элемента по строке. Он эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге проводится соответствующая перенумерация переменных. Метод Гаусса с выбором главного элемента по столбцу эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация строк. Иногда применяется и метод Гаусса с выбором главного элемента по всей матрице, когда в качестве ведущего выбирается максимальный по модулю элемент среди всех элементов матрицы системы. Нахождение матрицы, обратной матрицы A, эквивалентно решению матричного уравнения  (3)где E – единичная матрица и X – искомая квадратная матрица. Пусть  ,  . Уравнение (3) можно записать в виде системы  уравнений (4)где  при  и  при  . Далее, можно заметить, что система (4) распадается на n независимых систем уравнений с одной и той же матрицей A, но с различными правыми частями. Эти системы имеют вид (5)где  , у вектора  равна единице j-я компонента и равны нулю остальные компоненты.Указания и требования. 1) Требуется решить систему линейных уравнений с выбором главного элемента по строкам или столбцам:
– метод и система определяются преподавателем. 2) Вычислить вектор невязки  , где  – полученное решение.3) Вычислить определитель матрицы  используя метод Гаусса.4) Найти обратную матрицу  используя метод Гаусса.5) Сделать проверку, умножить матрицу на полученную матрицу .6) Оформить отчет. В отчете должна быть приведена постановка задачи, описан алгоритм решения задачи и приведена теоретическая задача, с подробным решением (дается преподавателем). Литература Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: «Наука», 1970. Самарский А.А., Гулин А.В. Численные методы. – М.: «Наука», 1989. |
