Основы матричного анализа
 Скачать 82.96 Kb.
|
|
Министерство образования Республики Беларусь Учреждение образования «Полоцкий государственный университет» Радиотехнический факультет Кафедра энергетики и электроники Практическое занятие №1 Цифровая обработка сигналов как задача вычисления векторно- матричного произведения. по дисциплине «Основы матричного анализа» Выполнил: Булгак А.А. Группа 17-РТ Проверил: Иванова К.И. Новополоцк 2018 г. Вариант:15 Цель работы: Провести анализ и формализацию задачи синхронизации бинарного сигнала с позиций векторно-матричной алгебры. №1 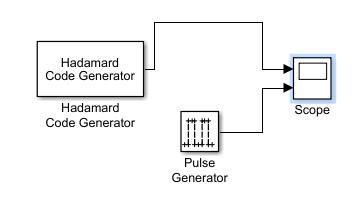 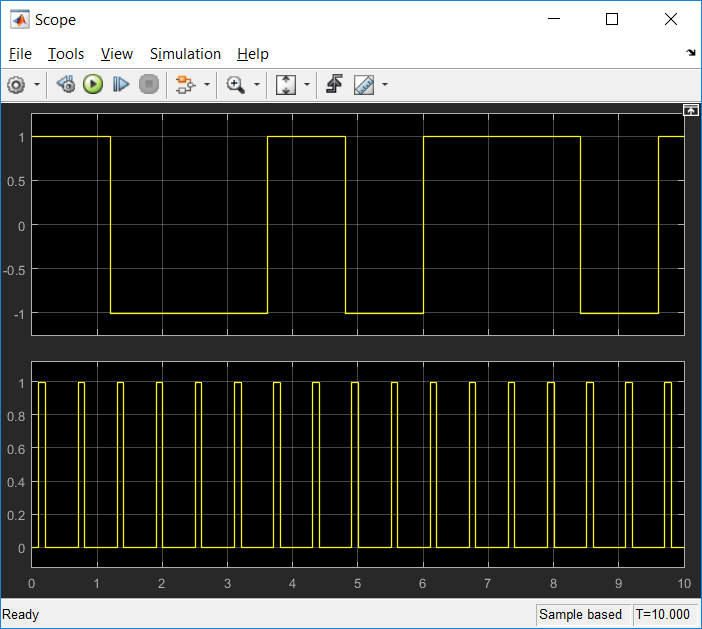 Вектор представляется в двоичном виде в алфавите (0=-1, 1=1): 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1 В программе Matlab пишем код:  В результате получаем код сигнала: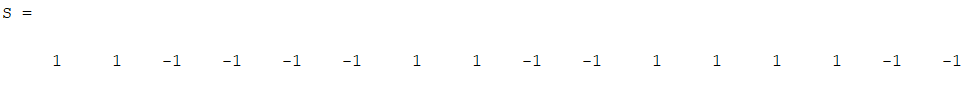 №2 Выводим матрицу Адамара в Matlab Код программы:  Результат: 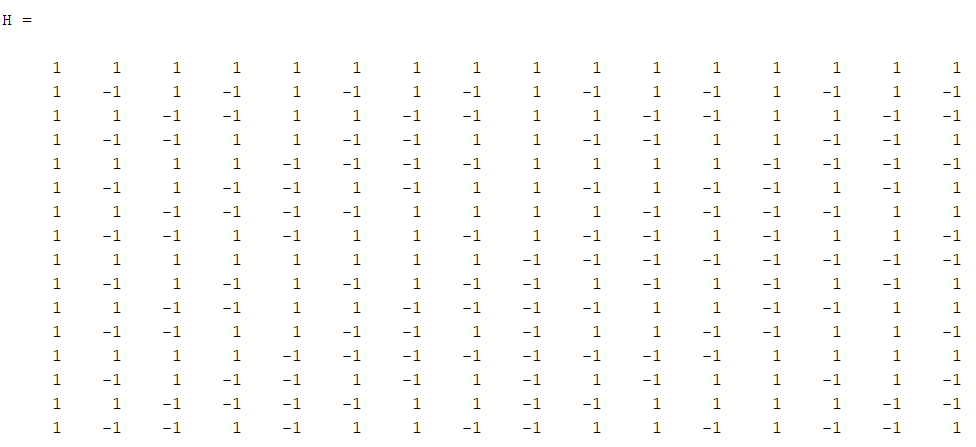 Из пятнадцатой строки матрицы Адамара, получим матрицу- циркулянт, используя программу Matlab: Код программы: H=hadamard(16) i=14 S=H(i+1,:) C(1:)=S For n=2:16 C(n,:)=[C(n-1, 16) C(n – 1,1:15)] end Результат:  Возьмем пятнадцатую строку матрицы- циркулянта, и получим следующий результат: 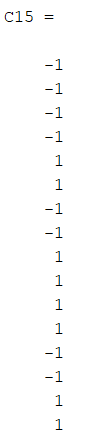 Далее считаем корреляцию, умножив матрицу- циркулянт на полученный столбец: Код программы: >> H=hadamard(16) i=14 S=H(i+1,:) C(1:)=S For n=2:16 C(n,:)=[C(n-1, 16) C(n – 1,1:15)] End M=C*C (i-12,:)’ Результат: M= 4 16 4 -8 -4 0 4 8 -4 -16 -4 8 4 0 -4 -8 Вывод: При произведении матрицы- циркулянта на вторую строку получили корреляцию. Местоположение корреляционного максимума соответствует местоположению обнаруживаемого сигнала. При этом величина максимума корреляции служит мерой близости входного сигнала и эталонов. |