лаба. Лабораторная работа 1 испытание на растяжение до разрушения образца из малоуглеродистой стали. Механические характеристики материалов

• Название: Лабораторная работа 1 испытание на растяжение до разрушения образца из малоуглеродистой стали. Механические характеристики материалов
• Дата: 11.12.2021
• Размер: 312 Kb.
• Имя файла: Laba__1 (1).doc
• Тип: Лабораторная работа; #300480

Лабораторная работа № 1
ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ ДО РАЗРУШЕНИЯ ОБРАЗЦА ИЗ МАЛОУГЛЕРОДИСТОЙ СТАЛИ. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
Цель работы:1) изучение поведения стального образца при растяжении до разрушения;

2) получение диаграммы растяжения и установление ос­новных механических

характеристик прочности и плас­тичности.

1. 
   Общие положения
   

Испытание на растяжение является наиболее распространен­ным видом испытания материалов, так как при нем наиболее яр­ко выявляются характеристики прочности и пластичности мате­риалов.

Методы испытаний на растяжение черных и цветных метал­лов и изделий из них регламентируются ГОСТом 1497-84.

При статических испытаниях на растяжение определяются следующие основные механические характеристики материалов:

предел пропорциональности – σ_пц;

предел упругости – σ_у;

предел текучести физический — σ_т;

временное сопротивление – σ_в;

отно­сительное удлинение после разрыва – ε_;

относительное сужение поперечного сечения после разрыва – ψ_;

истинный предел про­чности – σ_ист;

удельная работа, затраченная на разрыв –а.

Испытание на растяжение является одним из основных видов механических испытаний, позволяющих определять указанные выше характеристики материалов. Производятся аналогичные испыта­ния и для других видов деформирования. Такое испытание заклю­чается в статическом растяжении образца вплоть до его разру­шения. Статическим называют нагружение, при котором усилие к испытываемому образцу прикладывается медленно, с постепенным непрерывным нарастанием, без толчков и ударов.

Эксперименты произ­водятся на образцах из различных материалов при температуре окружающей среды.

Для сравнимости механических характеристик, получаемых при испытаниях, используются специальные образцы, форма и размеры которых предусмотрены ГОСТом.

Образец должен обладать такой формой, чтобы в пределах оп­ределенной части его объема во время испытания осуществлялось линейное напряженное состояние (центральное растяжение). Эта часть образца носит название рабочей части. Она представляет собой стержень прямоугольного или чаще круглого постоянного поперечного сечения с прямой осью. Силы, растягивающие образец, прикладываются в центре тяжес­ти двух концевых сечений рабочей его части по одной прямой. Это обеспечивается симметричной формой головок образца, встав­ляемых в зажимы испытательных машин.

Обеспечение линейного на­пряженного состояния дает возможность пользоваться для подсче­та напряжений простейшей формулой.

2. 
   Образцы для испытаний на растяжение
   

Размеры и типы образцов установлены ГОСТом 1497-84, а правила отбора образцов установлены ГОСТом 7564-73. Для испытаний применяют цилиндрические образцы диаметром d₀ от 3 мм и более (рис. 1,а) или плоские толщиной а₀ от 0,5 мм и более (рис. 1,б), с на­чальной расчетной длиной для цилиндрических образцовl₀ = 5d₀ (короткие образцы), l₀ = 10d₀ (длинные).



Рис. 1. Образцы для испытания на растяжение по ГОСТ 1497-84:

а) цилиндрический; б) плоский.
Для плоских длинных образцовl₀ = 11,3√А₀, для плоских коротких образцовl₀ = 5,65√А_0,

где А₀ — первоначальная площадь поперечного сечения образца.

Применение коротких образцов предпочтительнее.
1.3. Подготовка образцов к испытанию
Размеры поперечного сечения образца измеряют с погрешно­стью до 0,01 мм, рабочую длину образца l с погрешностью до 0,1 мм. На рабочей длине образца с помощью делительной ма­шины ДМ наносят риски, таким образом, отмечая начальную расчетную длинуl₀.

Измерение поперечных размеров образца проводят в трех местах: в средней части и на границах рабочей длины образца. По наименьшему из полученных результатов измерений определяют начальную площадь А₀ в его рабочей части с отклонением не бо­лее 0,01 мм².
1.4. Испытательные машины
Испытания на растяжение осуществляется на серийно выпус­каемых испытательных машинах, которые должны соответствовать требованиям ГОCT 7855-84.

При проведении испытаний на растяжение можно исполь­зовать испытательные машины ИМ-4Р, ИМ-4А, WPM-1000 (Германия, рис. 2) или другие испытательные машины с механи­ческим или гидравлическим приводом, имеющие диаграммный аппарат для регистрации результатов испытаний. При вычерчивании диаграммы растяжения по вертикаль­ной оси откладывается нагрузка, по горизонтальной - абсолют­ное удлинение.

При испытании на растяжение записывают кривую измене­ния величины абсолютного удлинения образца в зависимости от нагрузки, действующей на образец. Диаграмма растяжения мало­углеродистой стали приведена на рис. 3.

Рис. 2. Разрывная машина WPM-1000 (Германия).
1.5. Подготовка и проведение испытаний
1. Измерить поперечные размеры образца.

2. Отметить на поверхности образца расчетную длину.

3. Проверить готовность к испытанию машины и диаграммного аппарата.

4. Установить образец в захваты испытательной машины.

5. Включить нагружающее устройство испытательной машины и, плавно нагружая образец, провести его испытание до раз­рушения. При испытании скорость перемещения подвижно­го захвата машины не должна превышать:

до предела текучести — 2 мм/мин, за пределом текучести - 10 мм/мин.

6. В процессе испытания наблюдать за поведением образца, ав­тозаписью диаграммы растяжения и внимательно следить за показаниями стрелки силоизмерительного устройства маши­ны. При проведении испытания необходимо зафиксировать:

• нагрузку F_т, соответствующую физическому пределу теку­чести (стрелка силоизмерителя на короткое время явно ос­танавливается, а на автодиаграмме появляется площадка текучести);

• максимальную нагрузкуF_в соответствующую пределу проч­ности (временному сопротивлению). Максимальная нагруз­ка определяется по контрольной стрелке силоизмерителя;

• нагрузку в момент разрываF_р, соответствующую истинно­му сопротивлению разрыву.

7. После разрушения образца выключить испытательную маши­ну, извлечь из захватов обе половины образца и снять авто­диаграмму;

8. Произвести обмер разрушенного образца. Для этого плотно сложить обе части образца так, чтобы их оси образовали пря­мую линию, и измерить штангенциркулем длину расчетной части образца после разрываl_1,а также минимальные разме­ры образца в месте разрыва (в шейке).

9. Определить площадь поперечного сечения в «шейке».

10. Результаты испытаний записать в соответствующие графы протокола.
1.6. Анализ диаграммы растяжения
Рассмотрим основные осо­бенности, характерные точки и участки диаграммы растяжения.

Вначале испытания на диаграмме растяжения наблюдаются не­большие горизонтальный и криволинейный участки, которые объясняются обтяжкой всех устройств и устранением зазоров в механизмах машины, а также между головками образца и захватами машины. Вслед за этим кри­волинейным участком наблюдается быстрое возрастание нагрузки. На диаграмме при этом вычерчивается прямая линия ОА, соответ­ствующая пропорциональной зависимости между нагрузкой и удли­нением образца (деформацией). Эта прямолинейная зависимость отражает закон пропорциональности - закон Гука.

Прямолинейный участок диаграммы продолжается до некоторой точки А, за которой прекращается действие закона Гука. Нагруз­ка F_пц, соответствующая точке А, служит для вычисления предела пропорциональности. Точка А (рис. 3) соответствует напряжению предела пропорци­ональности σ_пц.

Предел пропорциональностиσ_пц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):

(1)

Площадь поперечного сечения образца на участке ОА практичес­ки не изменяется.

Если приостановить испытание при нагрузке, меньшей F_пциразгрузить образец, то можно заметить линейную зависимость Δl= f(F), и в процессе разгрузки она будет выражаться той же прямой АО. Следовательно, процесс разгрузки подчиняется зако­ну Гука. Причем после разгрузки полностью восстановятся пер­воначальные размеры и форма образца. Таким образом, в данный момент наблюдаются лишь упругие деформация. Отсюда зона ОА именуется зоной упругости материала.

В непосредственной близости от точки А находится точка В, соответствующая пределу упругости σ_у.



Рис. 3. Диаграмма растяжения малоуглеродистой стали.
Предел упругости σ_у — напряжение, после которого появляется остаточное удлинение.В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу про­порциональности.

За точкой А на диаграмме растяжения закон пропорциональнос­ти сначала нарушается, а после некоторой точки В наблюдается рост деформации без заметного возрастания растягивающей силы и на диаграмме появляется криволинейный участок. За­тем криволинейная часть диаграммы переходит в почти горизон­тальный участок — площадку текучести. Здесь деформации рас­тут практически без увеличения нагрузки (участок ВС).

Здесь обнаруживается процесс текучести материала: усилие в основном неизменно, в то вреда как удлинение существен­но возрастает. В период текучести материал претерпевает существенные структурные изменения, обусловленные массовы­ми сдвигами отдельных его частиц. Если поверхность образца пред­варительно тщательно отшлифована, то в период текучести можно заметить ее потускнение, а в увеличительное стекло увидеть сет­ку из мелких линий, наклоненных под углом, близким к 45°, так как по этим площадкам действуют максимальные касательные напря­жения. Эти линии представляет собой следы смещения отдельных частиц материала, обусловленного большими деформациями образца. Они называются линиями Чернова по имени знаменитого русского металлурга, впервые обнаружившего их.

В период текучести происходит накопление пластических смещений металла по наклонным сечениям, которые переходят в необратимые структурные изменения материала, определяемые как самоупрочнение испытываемого образца.

Соединение железа с углеродом представляет прочные включения, образующие в смеси с железом тонкие прослойки на поверхности кристаллических зерен, состоящих из чистого же­леза, и образуют так называемую перлитовую решетку. В начале загружения стали нагрузка воспринимается в основном пер­литовыми прослойками, пока при достижении предела пропор­циональности не начнется их постепенное разрушение.

В процес­се текучести наблюдается массовое разрушение перлитовой ре­шетки, в результате которого происходят большие пластические деформации ферритовых зерен, выражающиеся в сдвигах по косым площадкам внутри зерен. Внешне эти сдвиги проявля­ются на поверхности шлифованного образца в виде так называе­мых линий Чернова.

Явление текучести присуще небольшой группе сталей с содержанием углерода 0,1…0,3%. При большем содержании углерода перлитовая решетка оказывается настолько прочной, что массового разрушения ее не происходит. То же наблюдается при испытании многих легиро­ванных сталей, поэтому площадка текучести в диаграмме теку­чести этих сталей отсутствует. В сталях с малым содержанием углерода перлитовая решетка не оказывает значительного со­противления и площадка текучести также не возникает.

Приведем некоторые механические характеристики распространенных марок сталей.
Характеристики Марки сталей
Ст. 2 Ст. 3 Ст. 4

Относи­тельное остаточное удлинение, % 26 21 19

Предел прочности, кГ/мм² 38 44 52

Предел текучести, кГ/мм² 23 33 40
Часто понимают, что относительное остаточ­ное удлинение должно быть не больше указанных значений. По­этому следует пояснить, что чем больше пластичность стали, тем лучше она сопротивляется ударным, переменным и различным случайным воздействиям, и поэтому желательно, чтобы пластич­ность стали была как можно выше.

Точка С соответствует пределу текучести σ_т.

Предел текучестиσ_т — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):

(2)

Зона ВС называется зоной общей текучести. На участке текучести ВС происходит существенная пластичес­кая деформация порядка 1…2 %.

Известно, что не любые материалы имеют в процессе деформирования ярко выраженную площадку текучести на кривой растяжения. Такие материалы, как дюралюминий, легированные стали, стали с повышенным содержанием углерода и другие, практически не имеют площадки текучести. Заметим, что у стали в обычных условиях склонной к текучести, после холодной или тепловой обработки давлением явление текучести может не наблюдаться.

На рис. 4 показаны примерные диаграммы растяжения для стали 45 и стали 30, на которых не обнаруживаются площадки теку­чести.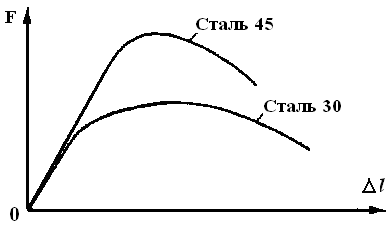


Рис. 4. Диаграммы растяжения многоуглеродистой стали.
В таких случаях следует определять условный предел текучес­ти - это то напряжение, при котором относительное удлинение дос­тигает 0,2 % от длины расчетной части образца. Для вычисления условного предела текучести на оси абсцисс в масштабе, соответ­ствующем диаграмме, откладывается величина, равная 0,002l₀Затем, учитывая то обстоятельство, что при разгрузке материал подчиняется закону Гука, проводится линия параллельно участку упругости ОА (рис. 5), На пересечении этой прямой, (на рис. 5 она изображена пунктиром) с диаграммой растяжения получается точка С, ордината которой и определяет нагрузку F₀₂, соответствующую условному пределу текучести σ₀₂, равному σ₀₂ = F₀₂/А₀.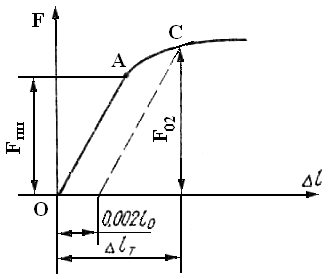


Рис. 5. Разгрузка материала.
После завершения текучести дальнейшее деформирование про­исходит при увеличении нагрузки, так как материал упрочнился, приобрел возможность опять сопротивляться возрастающей нагруз­ке до значенияF_max. Прямой пропорциональности здесь уже не наблюдается, а ди­аграмма имеет криволинейный характер c максимумом в точке D (точка D на диаграмме соответствует напряжению предела прочности — временного сопротивления σ_в).

Временное сопротивление σ_вявляется основным показателем прочности материала и представляет собой наибольшее напряже­ние, которое выдерживает материал перед разрушением (МПа):

⁽³⁾

Зона CD называется зоной распределения. До точки D удлине­ние образца происходит по всей длине. В процессе эксперимента можно наблюдать, что за пределом прочности поперечные деформации в образовало его объему рас­пределяются не равномерно, а сосредоточиваются в одном, самом слабом месте. При достижении макси­мальной нагрузки на образце образуется местное утоньшение, именуе­мое «шейкой». По мере дальнейшего растяжения сечение шейки умень­шается и, наконец, происходит разрушение образца. За точкой Dнагрузка, приходящаяся на образец, падает, так как при уменьшении поперечного сечения образца в области шейки требует­ся меньшая сила для его разрыва, т.е. F_р < F_В, Дальнейшее растяжение происходит в зоне шейки, после чего наступает раз­рушение образца (точка К соответствует истинному пределу про­чности σ_ист):

(4)

где А_к - площадь поперечного сечения образца в месте разрыва (шейки), мм².

Если в процессе испытания за площадкой текучести разгрузить образец, скажем в произвольной точке Nдиаграммы (рис. 6),то разгрузка будет идти по прямой, параллельной упругой линии ОА, ввиду справедливости закона Гука при разгрузке. Это показы­вает, что в рассматриваемый момент испытания в образце наблюдаются упругие (отрезок RM)и пластические (отрезок OR)де­формации. Если же образец подвергнуть повторному нагружению, то оно не будет практически совладать с прямой NRразгрузки. Образуется некоторая "петля". Ее возникновение связано с необ­ратимыми потерями энергии в материале образца, к которым сле­дует еще добавить и влияние люфтов в испытательной машине и в диаграммном устройстве. При повторном нагружении получается укороченная диаграмма растяжения (рис. 6, б) с повышенным значением F_пци F₀₂,а также с уменьшенной величиной оста­точной деформации. Таким образом, в результате предварительно­го пластического деформирования материал становится иным с дру­гими механическими характеристиками: повышенными σ_пц,σ₀₂и уменьшенной пластичностью. Такое явление носит название накле­па.

Рассматриваемое при испытании стали явление наклепа часто объясняется как упрочнение в процессе загружения за пределом текучести. Такое объяснение верно с той точки зрения, что за предельное напряжение для стали обычно принимается предел текучести. Так как при наклепе площадка текучести ис­чезает, а условный предел текучести повышается, допускаемое напряжение или расчетное сопротивление могут быть повыше­ны. Однако выражение «повышение прочности» иногда создает неправильное представление об увеличении предела прочности при наклепе. Оно основано на неправильном понима­нии причин явления наклепа. Иногда понимают наклеп как результат разгрузки, которая производится для установле­ния изменения свойств стали при наклепе. Поэтому необходимо помнить о необратимых изменениях, происходящих в структуре стали при загружении, рассмотренных выше. Они, а не разгрузка, являются причиной наклепа. Разгрузка же и повтор­ное загружение позволяют проследить за этими изменениями. Часть диаграммы, соответствующая дальнейшему загружению, вместе с ее характеристикой — пределом прочности — остается без изменения. Поэтому лучше явление наклепа характеризо­вать не как упрочнение, а как изменение свойств стали при за­гружении за пределом текучести, которое выражается в увели­чении предела пропорциональности и в ухудшении важнейшей характеристики пластичности — в уменьшении относительного остаточного удлинения.

Нередко путают явление наклепа с упрочнением ма­териала в шейке при разрыве. Это явление носит другой харак­тер и имеет другие причины, при этом материал в шейке именно получает упрочнение, так как предел прочности его увеличива­ется в два-три раза. Это устанавливается путем определения истинных напряжений при разрыве. Иногда возникает сомнение: можно ли считать, что материал в шейке выдержал эти большие напряжения, если именно в этом месте и произошел разрыв. Но если перед самым разрушением снять нагрузку, образец с образо­вавшейся шейкой останется неразрушенным, следовательно, мате­риал в шейке выдержал действовавшую в этот момент нагрузку.

Можно привести практические примеры применения явления упрочнения материала в шейке. Аналогичное упрочнение наблю­дается при калибровании и холодном волочении проволоки, т. е. при пропускании ее через ряд уменьшающихся отверстий. При­меняемая в железобетонных предварительно напряженных кон­струкциях высокопрочная проволока изготовляется таким путем из высокоуглеродистой стали. Ее нормативное сопротивление, или браковочный минимум, по пределу прочности при диаметре 5 ммсоставляет 17 000 кГ/см²,а при диаметре 3 мм— 19 000 кГ/см². Увеличение числа операций по калиброванию приводит к дальнейшему увеличению прочности.

Дамасская сталь или булат, а также применявшаяся для ружейных стволов так называемая «букет­ная сталь» тоже делалась из проволоки, сваренной кузнечным способом в цельный кусок металла, что сообщало стали дополни­тельную прочность.

По диаграмме растяжения можно подсчитать полное удлинение образца в момент разрыва. На диаграмме оно выражается отрезком ОО₂(см. рис. 3).Чтобы выделить остаточную иди упругую де­формацию, достаточно из точки К провести прямую КО₁ ׀׀OA. Тогда отрезок OО₁будет представлять собой остаточную деформацию в момент разрыва образца, а отрезок О₁О₂ - упругую деформацию. Последняя исчезает после разрыва образца. Остаточная же остается, благо­даря чему удлинение, вычисленное как разность между длиной, l разорванного образца, полученной путем непосредственного заме­ра его OО₁после окончания эксперимента, и начальной длиной l₀, соответствует на диаграмме отрезку OО₁.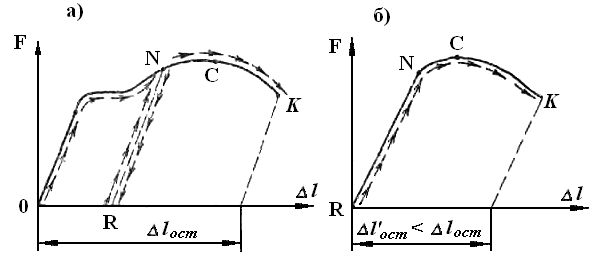


Рис. 6. Повторное нагружение образца.
Величины остаточных деформаций в момент разрушения образца (удлинение, сужение) служат мерой пластичности материала. Таким образом, в процессе испытания образцов на растяжение можно получить характеристики пластичности материала: остаточное удлинение образца после разрыва ε, % и остаточное относительное сужение ψ, %_.

Чем больше эти величины, тем материал пластичней.

Интересен характер разрушения образца из малоуглеродистой стали (рис. 7, а). В месте разрыва образуется "чашечка",так как поверхность разрушения состоит из двух зон: центральной поверхности (дно чашечки), которая перпендикулярна оси образца и краевой, конической, наклоненной к оси образца под углом 45°. Это объясняется наличием сложного напряженного состояния в об­ласти шейки образца. Исследования показывают, что в плоскости поперечного сечения шейки напряжения распределены по сложному параболическому закону с максимумом на оси образца. Поэтому разрыв образца из пластичного материала и начинается с централь­ной части. Оставшаяся кольцевая часть образца разрушается от наибольших касательных напряжений. Такой тип разрушения приня­то называть разрушением путем сдвига или вязким разрушением.

Для сравнения на рис. 7, б показан характерный вид раз­рушения цилиндрических образцов из хрупких материалов. Такие материалы при растяжении разрушаются по плоскости поперечного сечения. Этот тип разрушения называется хрупким разрушением или разрушением путем отрыва.

Испытание хрупких материалов на растяжение обычно не производится, так как в конструкциях хрупкие материалы ис­пользуются, как правило, при работе на сжатие. Разрыв таких материалов происходит при небольших удлинениях и без образования шейки.


Рис. 7. Разрушение пластичного а) и хрупкого б) материалов.
По диаграмме растяжения можно подсчитать работу, затрачен­ную на разрыв образца. Она выражается площадью диаграммы, за­ключенной между кривой деформирования ОАВСDК (рис. 3) и осью абсцисс. Чем больше работа, затраченная на разрыв образ­ца, тем больше энергии может поглотить образец без разрушения и тем лучше он будет сопротивляться ударным нагрузкам. Для по­лучения величины, характеризующей не образец, а его материал, подсчитывается удельная работа разрыва а, т.е. количество работы, приходящееся на единицу объема образца:

₍₅₎

Площадь диаграммы растяжения (т.е. полная работа А) может быть определена при помощи различных методов, в том числе приближенных. Один из них заключается в применении формулы вида

A = ηΔl_р· F_В , ₍₆₎

где η - коэффициент полноты диаграммы. Он зависит от мате­риала образца. Этот коэффициент показывает, какую часть площа­ди огибающего диаграмму прямоугольника OLNTсоставляет диаг­рамма растяжения (рис. 8,а). Для пластичных сталей коэффи­циент η принимается в пределах 0,8…0,9. В частности, для малоуглеродистой стали он равен 0,85.


Рис. 8. Определение полной работы.

Площадь диаграммы растяжения можно подсчитать и путем сум­мирования площадей отдельных простейших фигур, на которые пред­ставляется возможным разбить эту площадь. С достаточной степенью точности площадь диаграммы растяжения можно представить в виде прямоугольника ω₁ и параболы ω₂ (рис. 8,б).

Тогда


или

(7)

В таблице приведены ориентировочные значения механи­ческих характеристик и характеристик пластичности для некоторых распространенных материалов.

Материал	σТ · 108 Па	σВ · 108 Па	ε, %	ψ, %
Сталь 08	2,0	3,2…4,0	33	60
Сталь 10	2,1…2,2	3,4…4,2	32	55
Сталь 15	2,3	3,8…4,5	31	55
Сталь 20	2,3…2,5	4,0…5,0	31	50
Сталь 25	2,4…2,6	4,2…5,2	27	50
Сталь 30	2,7…3,0	5,0…6,0	25	50
Сталь 35	3,0…3,2	5,4…6,6	24	45
Сталь 40	3,3…3,5	5,8…7,2	24	45
Сталь 45	3,6	6,1…7,6	19	40
Сталь 50	3,8	6,4…8,0	17	40
Сталь 55	3,9	6,6…8,3	16	35
Сталь 60	4,1	6,9…8,5	14	35
Сталь 65	4,2	7,1…7,2	10	30
Сталь 70	4,3	7,3	9	30
Сталь хромистая 15Х	5,0	7,0	16	50
Сталь марганцевистая 25Г	3,0	5,0	26	50
Сталь марганцевистая 30Г	3,2	5,5	24	45
Сталь марганцевистая 60Г	4,2	7,1	11	35
Сталь марганцевистая 65Г	4,4	7,5	9	30
Сталь марганцевистая 40Г2	3,9	6,7	14	40
Сталь марганцевистая 50Г	4,0	6,6	16	25
Сталь хромомолибденовая	3,0	8,0	14	50
30ХГСА	8,5	11,0	10	40
Медь	2,9	3,0	28	80
Дюралюминий	3,8	5,0	20	25

По оси абсцисс диаграммы растяжения определяются харак­теристики пластичности образца.

Полная деформация образца ∆l_полн складывается из остаточной деформации ∆l_ост (ОО₁ на рис. 3), не исчезающей после разрушения и упругой деформации ∆l_У (отрезок О₁О₂), исчезающей после разрушения образца:

∆l_полн = ∆l_ост + ∆l_У (5)

Относительное удлинение ε — отношение абсолютного удлине­ния к первоначальной длине, выраженное в процентах:

(6)

Относительное сужение ψ — отношение уменьшения площади поперечного сечения образца после разрушения к первоначальной площади поперечного сечения, выраженное в процентах:

(7)

Работа стали в конструкциях допускается, как правило, с напряжениями, значительно мень­шими предела пропорциональности, и использование остальной криволинейной части диаграммы возможно лишь в отдельных точках элементов конструкций, например в местах концентрации напряжений, ударных воздействий.
1.7. Обработка результатов
По диаграмме растяжения определяются механические харак­теристики: σ_пц, σ_т, σ_в, σ_ист, ε, ψ.

1. На диаграмму наносят координатные оси. Ось абсцисс сов­мещают с нулевой линией диаграммы, а для проведения оси ординат находят начало координат - точку О, продолжая прямолинейный участок диаграммы до пересечения с осью абсцисс. Таким образом, из рассмотрения исключается на­чальный криволинейный участок диаграммы, который воз­никает вследствие первоначального обмятия головок образца в захватах машины.

2. Определить масштаб записи диаграммы по оси нагрузок μ_F, кн/мм. Для этого величину максимальной нагрузкиF_max кН, определенной по шкале силоизмерительного прибора, делят на ординату точки D, мм, диаграммы растяжения.

3. Для определения величиныF_пц ординату точки А умножают на масштаб μ_F, кн/мм. Предел пропорциональности σ_пц вычис­ляют по формуле (1).

4. Для определения нагрузки, соответствующей площадке теку­честиF_т, ординату точки С, мм, умножают на масштаб по оси нагрузок μ_F, кн/мм. Затем по формуле (2) вычисляют предел текучести σ_т.

5. По формуле (3) вычисляют временное сопротивление σ_в.

6. Разрушающую нагрузкуF_р, соответствующую точке К, опре­деляют, умножив ординату этой точки на масштаб μ_F. По формуле (4) вычисляют истинное сопротивление разрывуσ_ист.

7. Определяют остаточное удлинение образца ∆l_ост = ∆l_к + ∆l_У, мм.

8. Относительное удлинение ε определяется по формуле (6).

9. Относительное сужение ψ определяется по формуле (7), где А_к — площадь поперечного сечения образца в месте разрыва (шейки), мм².

1.8. Журнал испытаний
Эскизы образцов до и после испытаний

Образец	Эскизы образцов до испытаний	Эскизы образцов после испытаний
Цилиндрический образец
Плоский образец

Размеры цилиндрического образца до испытания

Начальный диа­метр, d0 мм	Начальная расчетная длина, l0 мм	Начальная площадь попе­речного сечения, А0 мм2

Размеры плоского образца до испытания

Начальные размеры			Начальная площадь попе­речного сечения, А0 мм2
а0, мм	в0 = За0, мм	l0 мм

Размеры цилиндрического образца после испытаний

Диаметр в месте шейки, после разрыва, dK, мм	Конечная расчет­ная длина,lк мм	Конечная площадь попе­речного сечения, Ак мм2

Размеры плоского образца после испытаний

Конечные размеры образца			Конечная площадь поперечного сечения в месте шейки, Ак мм2
а0, мм	вк, мм	lк, мм

Диаграмма растяжения


Результаты испытаний образцов при растяжении

	Fпц, кН	Fт, кН	Fmax, кН	Fр, кН	σпц, МПа	σт, МПа	σв, МПа	σр, МПа
Цилиндрический
Плоский

	∆lост, мм	ε, %	∆А, мм2	ψ, %
Цилиндрический
Плоский

Контрольные вопросы
1. Какова цель испытания материалов на растяжение?
Определить основные механические характеристики металлов
2. Какую форму имеет образцы для испытания на растяжение металлов? Чем объясняется принимаемая форма образцов?
Как правило сечения с одинаковой площадью поперечного сечения вдоль всего образца, цилиндрические, призматические, плоские
3. Какие механические характеристики материалов характери­зуют его прочность?
Прочность - это возможность сопротивляться напряжению от нагрузки без разрушения, соответственно основной характеристикой прочности является временное сопротивление, а также истинный предел про­чности – σ_ист, и условный предел прочности, принимаемый для расчетов
4. Какие параметры характеризуют пластические свойства ма­териалов?

Пластичность - это свойство материала менять форму при приложении нагрузки и оставлять эту форму после прекращения действия этой нагрузки, соответственно пластические свойства определяются Пределом текучести.

5. Чем характеризуются упругие и остаточные деформации?

Упругие деформации - пропадают при прекращении действия нагрузки, остаточные - нет.

6. Как по диаграмме растяжения образца определить величину остаточной и упругой деформации в любой момент испыта­ния?

7. Сформулируйте закон Гука. Для какого участка диаграммы справедлив закон Гука?

8. Как определяются предел пропорциональности, предел теку­чести, временное сопротивление?

9. Что такое условный предел текучести и как его определяют?

10. Какова природа возникновения линий Чернова?

11. На каком участке диаграммы в образце обнаруживается шей­ка?

12. Что такое фиктивное и действительное напряжения в момент разрыва? Какое из них оказывается большим?

13. Как определяется удельная работа деформации растяжения и что она характеризует?

14. Как определяется по диаграмме растяжения остаточная де­формация в момент разрыва?

15. Что такое наклеп и как его можно использовать в тех­нике?

16. Как разрушаются образцы из хрупкого и пластичного метал­лов? В чем различия между характером разрушения этих материалов?