Лабораторная работа 1 Исследование движения тела под действием постоянной силы
 Скачать 0.69 Mb.
|
Вывод:_______________________________________________________________________________________________________________________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ Вопросы для защиты работы1. Изложить цель работы. 2. Опишите рабочую установку и ход эксперимента. 3. Поясните смысл и метод определения всех величин, вносимых в таблицу.
ЛАБОРАТОРНАЯ РАБОТА № 3 Сохранение механической энергии при движении тела под действием силы упругости и силы трения Цель работы: исследовать явление превращения потенциальной энергии упругой деформации пружины в кинетическую энергию поступательного движения тела. Оборудование: два штатива, динамометр, шар с отверстием, нить, линейка, белая и копировальная бумага, весы, гири. Теоретическая часть По закону сохранения и превращения механической энергии при любых взаимодействиях тел силами всемирного тяготения и упругости механическая энергия системы тел не изменяется. Поэтому если скорость некоторого тела изменяется под действием пружины, то изменение кинетической энергии тела ∆Еk должно быть равно изменению потенциальной энергии пружины с противоположным знаком: ∆Еk = - ∆Ер , ∆Еk + ∆Ер = 0. Если пружина жесткостью k имеет деформацию х , то ее потенциальная энергия упругой деформации равна : Ер = 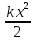 .Если потенциальная энергия полностью расходуется при взаимодействии пружины жесткостью k и тела массой m , то это тело из состояния покоя должно приобрести такую скорость , при которой выполняется равенство 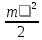 = 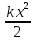Ход работы 1. Установил(а) динамометр и шар на одинаковой высоте h от поверхности стола. Нить длиной 60 – 80 см одним концом зацепить за крючок динамометра, другим концом привязать к шару. 2. Придерживая шар, отодвинул(а) штатив настолько, чтобы деформация пружины х была равна 10 см и снял(а) показания динамометра F . Определил(а) жесткость пружины 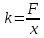 3. По найденной жесткости k пружины и её деформации x вычислил(а) изменение потенциальной энергии упругой деформации: ∆Ер = 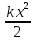.4. Отпустил(а) шар. В месте падения шара положить листы белой и копировальной бумаги. Место падения отмечается при ударе по копировальной бумаге. Повторил(а) опыт три раза. 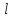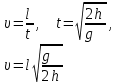Измерил(а) среднее значение дальности полёта  шара при падении с высоты h М 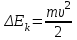 ассу шара измерил(а) с помощью весов.Вычислил(а) изменение кинетической энергии шара: Результаты измерений и вычислений занес в отчетную таблицу:
5. Сравнил(а) полученные значения и сделал(а) вывод. 6. Оценил(а) границы погрешности определения потенциальной энергии растянутой пружины и кинетической энергии шара. Вывод:________________________________________________________________ ________________________________________________________________ ________________________________________________________________ ________________________________________________________________ Контрольные вопросы Каким выражением определяется потенциальная энергия деформированной пружины? Каким выражением определяется кинетическая энергия тела? 3. При каких условиях выполняется закон сохранения механической энергии? Ответы на вопросы 1.___________________________________________________________________ ___________________________________________________________________ 2.___________________________________________________________________ ____________________________________________________________________ 3.___________________________________________________________________ ____________________________________________________________________
ЛАБОРАТОРНАЯ РАБОТА № 4 Измерение зависимости периода маятника от длины нити _____________________________________________________________________________ Цель работы: состоит в экспериментальной проверке формулы, связывающей период колебаний маятника с длиной его подвеса. Оборудование:штатив с перекладиной и муфтой, нить с петлями на концах, груз с крючком, линейка, электронный секундомер Теоретическая часть Рассмотрим колебания нитяного маятника, т.е. небольшого тела (например, шарика), подвешенного на нити, длина которой значительно превышает размеры самого тела. Если шарик отклонить от положения равновесия и отпустить, то он начнет колебаться. Сначала маятник движется с нарастающей скоростью вниз. В положении равновесия скорость шарика не равна нулю, и он по инерции движется вверх. По достижении наивысшего положения шарик снова начинает двигаться вниз. Это будут свободные колебания маятника. 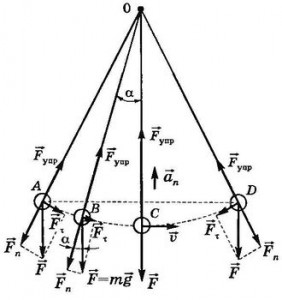 Свободные колебания – это колебания, которые возникают в системе под действием внутренних сил, после того, как система была выведена из положения устойчивого равновесия. Колебательное движение характеризуют амплитудой, периодом и частотой колебаний. Амплитуда колебаний - это наибольшее смещение колеблющегося тела от положения равновесия. Обозначается А. Единица измерения - метр [1м]. Период колебаний - это время, за которое тело совершает одно полное колебание. Обозначается Т. Единица измерения - секунда [1с]. Частота колебаний - это число колебаний, совершаемых за единицу времени. Обозначается ν. Единица измерения - герц [1Гц]. Тело, подвешенное на невесомой нерастяжимой нити называют математическим маятником.  Период колебаний математического маятника определяется формулой: 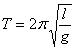 (1), где l – длина подвеса, а g – ускорение свободного падения. Период колебаний математического маятника зависит: от длины нити. Период колебаний математического маятника пропорционален корню квадратному из длины нити  . Например при уменьшении длины нити в 4 раза, период уменьшается в 2 раза; при уменьшении длины нити в 9 раз, период уменьшается в 3 раза. от ускорения свободного падения той местности, где происходят колебания. Период колебаний математического маятника обратно пропорционален корню квадратному из ускорения свободного падения 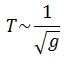 .Тело, подвешенное на пружине, называют пружинным маятником.  Период колебаний пружинного маятника определяется формулой  , где m - масса тела, k - жесткость пружины.Период колебаний пружинного маятника зависит: от массы тела. Период колебаний пружинного маятника пропорционален корню квадратному из массы тела  .от жесткости пружины. Период колебаний пружинного маятника обратнопропорционален корню квадратному из жесткости пружины 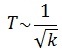 .В работе мы исследуем колебания математического маятника. Из формулы 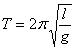следует, что период колебаний изменится вдвое при изменении длины подвеса в четыре раза.Это следствие и проверяют в работе. Поочередно испытывают два маятника, длины подвесов которых отличаются в четыре раза. Каждый из маятников приводят в движение и измеряют время, за которое он совершит определённое количество колебаний. Чтобы уменьшить влияние побочных факторов, опыт с каждым маятником проводят несколько раз и находят среднее значение времени, затраченное маятником на совершение заданного числа колебаний. Затем вычисляют периоды маятников и находят их отношение. ХОД РАБОТЫ 1. Подготовил(а) таблицу для записи результатов измерений и вычислений:
2. Закрепил(а) перекладину в муфте у верхнего края стержня штатива. Штатив разместил(а) на столе так, чтобы конец перекладины выступал за край поверхности стола. Подвесил(а) к перекладине с помощью нити один груз из набора. Расстояние от точки повеса до центра груза должно быть 25-30 см. 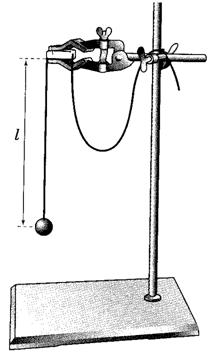 3. Подготовил(а) секундомер к работе в ручном режиме. 4. Отклонил(а) груз на 5-6 см от положения равновесия и замерил(а) время, за которое груз совершит 30 полных колебаний (при отклонении груза следил(а), чтобы угол отклонения не был велик). 5. Повторил(а) измерение 3-4 раза и определил(а) среднее время tср1=(t1+t2+t3+t4)/4 6. Вычислил(а) период колебания груза с длиной подвеса 25-30 см по формуле 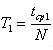 .7. Увеличил(а) длину подвеса в четыре раза. 8. Повторил(а) серию опытов с маятником новой длины и вычислил(а) его период колебаний по формуле  .9. Вычислил(а) частоты колебаний для обеих маятников по формулам  и  .10. Сравнил(а) периоды колебаний двух маятников, длины которых отличались в четыре раза, и сделал(а) вывод относительно справедливости формулы (1). 11. Ответил(а) на контрольные вопросы. Заполнил(а) таблицу: Результаты измерений
Вывод: __________________________________________________________________ __________________________________________________________________ __________________________________________________________________ __________________________________________________________________ Контрольные вопросы 1. Что называют периодом колебаний маятника? 2. Что называют частотой колебаний маятника? Какова единица частоты колебаний? 3. От каких величин и как зависит период колебаний математического маятника? 4. От каких величин и как зависит период колебаний пружинного маятника? 5. Какие колебания называют собственными? Ответы на вопросы: 1.___________________________________________________________________________________ ____________________________________________________________________________________ 2.___________________________________________________________________________________ ____________________________________________________________________________________ 3.___________________________________________________________________________________ ____________________________________________________________________________________ 4.___________________________________________________________________________________ _____________________________________________________________________________________ 5.___________________________________________________________________________________ _____________________________________________________________________________________
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
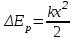