Лабораторная работа 1 Исследование движения тела под действием постоянной силы
 Скачать 0.69 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2 Изучение закона сохранения импульса Цель работы:экспериментальное исследование процесса соударения упругих тел и проверка выполнения в системе соударяющихся тел законов сохранения импульса и энергии. Оборудование:лабораторная установка FPM-08. Теоретическое введение В природе существует несколько законов сохранения, которые являются следствием свойств симметрии Вселенной. Известны законы сохранения энергии, импульса, момента импульса, электрического заряда, барионного числа (заряда), лептонного числа (заряда), четности и некоторых других величин. В механике фундаментальную роль играют первые три из перечисленных законов. Важность законов сохранения определяется следующими их свойствами. Законы сохранения не зависят от вида траектории и от характера действующих сил, поэтому они позволяют получать весьма общие и существенные выводы из уравнений движения. Законы сохранения могут быть использованы даже в тех случаях, когда силы не известны, как это имеет место в физике элементарных частиц. Законы сохранения помогают определить невозможные явления и указать неосуществимость разработки некоторых конструкций – например, вечного двигателя или спутника, приводимого в движение одними внутренними силами. В тех случаях, когда сила в точности известна, закон сохранения может оказать существенную помощь при решении задач о движении частиц. Для решения задач физики обычно следуют такому порядку: прежде всего один за другим применяются соответствующие законы сохранения, и только после этого, если в задачах ничего не упущено, переходят к решению дифференциальных уравнений, использованию вариационного принципа или метода возмущений, применению вычислительных машин и других средств. Напомним основные понятия, которыми мы будем здесь пользоваться. Механической энергией системы материальных точек или частиц называется следующая функция их координат и скоростей:  где тi,υi – соответственно масса и скорость i-ой материальной точки,  - некоторая функция взаимного расположения точек.Первое слагаемое в (1) называется кинетической энергией системы, а величина Ei=miυi2/2 – кинетической энергией материальной точки. Второй член в (1), т.е. называется потенциальной энергией системы. Эта величина зависит только от характера взаимодействия между частицами и их относительного расположения в системе. Например, потенциальная энергия материальной точки массой m, находящейся в поле сил тяжести на высоте h над поверхностью Земли, равна где g– ускорение свободного падения. А потенциальная энергия упругой силы  (3)Закон сохранения механической энергии утверждает, что для замкнутой системы частиц, в которой не действуют диссипативные силы, полная механическая энергия системы, определяемая формулой (1), остается постоянной во времени. Система является замкнутой, если на нее не действуют внешние силы. Диссипативными называются силы, работа которых при перемещении частиц зависит от пути, по которому происходит это перемещение. Действие диссипативных сил всегда связано с переходом механической энергии и другие виды энергии. Типичным примером диссипативных сил являются силы трения, сопротивления. В противоположность им консервативными называются силы, работа которых не зависит от формы пути, а зависит от начального и конечного положения частицы. Действие консервативных сил в системе не нарушает закон сохранения полной механической энергии. Консервативными силами является сила тяжести, упругие силы, гравитационные силы и др. Импульсом материальной точки или частицы массой т называется векторная величина  , равная Суммарный импульс системы, состоящей из п частиц:  где  - импульс i-ой частицы.В замкнутой механической системе сумма импульсов взаимодействующих частиц не меняется во времени. Это утверждение является законом сохранения импульса, т.е.  При соударении тела в большей либо меньшей мере деформируются. Абсолютно неупругим считается удар, после которого тела сохраняют деформацию и не восстанавливают первоначальную геометрическую форму. При этом кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. После удара тела движутся с одинаковой скоростью (т.е. как одно тело) либо покоятся. При неупругом ударе выполняется только закон сохранения импульса, а закон сохранения механической энергии не выполняется, т.к. механическая энергия переходит во внутреннюю. Абсолютно упругим называется такой удар, после которого тела восстанавливают первоначальную геометрическую форму и при котором деформация тел полностью исчезает. При абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии. Ниже проверяем эти законы на опыте для упругих ударов. Описание рабочей установки и метода измеренийПри абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии. Ниже проверяем эти законы на опыте для упругих ударов. Э 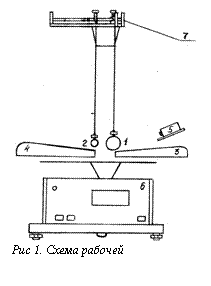 кспериментальные измерения импульса и механической энергии проводятся на установке FРМ-08, схема которой приведена на рис.1. Конструкция установки предусматривает возможность укрепления на длинных нитях металлических шаров 1 и 2. Стержни, на которых фиксируются шары, имеют заостренные концы, которые служат указателями для определения угла отклонения нити подвеса. Отсчет угла отклонения производится по шкалам 3 и 4. Один из шаров можно фиксировать в отклоненном положении с помощью электромагнита 5.Метод измерения импульса и кинетической энергии шаров до и после удара основывается на использовании закона сохранения механической энергии. Масса шаров измеряется взвешиванием на аналитических весах. Скорости же шаров в моменты времени непосредственно перед и после удара можно определить по углу отклонения нити подвеса. Действительно, в положении максимального отклонения полная энергия шара равна потенциальной энергии  , где  – масса шара,  – ускорение свободного падения,  – высота поднятия центра масс шара над уровнем положения равновесия (см.рис.2).Потенциальная энергия шара в нижней точке положения равновесия переходит в кинетическую энергию   тогда  Таким образом  Высоту можно найти, зная угол отклонения нити подвеса и длину подвеса  .Из чертежа на рис.1 видно, что  поэтому: 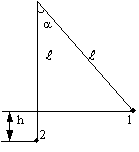  Рис. 2 Определяем импульсы шаров до  и после соударения  а так же кинетические энергии шаров до соударения  и после  .где  -скорость 1 шара до удара,  - скорость шара 1 после удара,  -скорость шара 2 после удара.При выполнении законов сохранения  и  .Ход работы1. Провел(а) корректировку осевой установки шаров. 2. Измерил(а) длину нитей от точки подвеса до метки на середине шаров.3. Ослабив фиксирующие гайки, установил(а) шкалы 3,4 таким образом, чтобы указатели подвесов занимали на шкалах нулевое положение, затянул(а) фиксирующие гайки. 4. Нажал(а) клавишу «СЕТЬ». 5. Отжал(а) клавишу «ПУСК». 6. Правый шар отодвинул(а) в сторону электромагнита и блокировал(а) его в этом положении, записал(а) значение угла отклонения подвеса правого шара от вертикали . 7. Нажал(а) клавишу «СБРОС». 8. Нажал(а) клавишу «ПУСК». 9. После столкновения шаров измерил(а) по шкале углы отклонения шаров  .10. Измерения повторил 3 раза. 11. Взвесил(а) шары на весах. 12. Вычислил(а) среднее значение <  > и< >.13. По формуле (8) вычислил(а) скорости шаров до и после соударения  14. Результаты занес(ла) в таблицу: 15. Поставив средние значения скорости шаров <υ>, <u1> и <u2> в (9 – 12), вычислил(а) сумму импульсов и кинетическую энергию до и после ударов. Затем сравнил(а) их значения. 16. Рассчитал(а) относительную погрешность формуле  .Таблица результатов
|