фИЗИКА. Лабораторная работа 1. Измерение линейных размеров и объемов твердых тел правильной формы студент гр. Фм1219
 Скачать 38.93 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Чувашский государственный университет имени И.Н. Ульянова» (ФГБОУ ВО «ЧГУ им. И.Н. Ульянова») Факультет прикладной математики, физики и информационных технологий Лабораторная работа №1. ИЗМЕРЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ И ОБЪЕМОВ ТВЕРДЫХ ТЕЛ ПРАВИЛЬНОЙ ФОРМЫ Выполнил: студент гр. ФМ-12-19 Кабаков Александр Владимирович Принял: доц. Петров Н. И. г.Чебоксары 2022. Приборы и принадлежности: штангенциркуль, микрометр, масштабная линейка, цилиндрическое кольцо. Цель работы – ознакомление с основными положениями теории погрешностей, статистической обработкой результатов измерений, а также правилами и приемами измерений линейных и угловых величин. Краткая теория: Для определения линейных размеров тел применяются самые различные измерительные приборы, выбор которых определяется необходимой точностью и условиями эксперимента. Наиболее простым их них является масштабная линейка с миллиметровыми делениями. Цена деления масштабной линейки 1 мм. При измерениях такой линейкой максимальная погрешность не превосходит половины цены деления, т.е. 0,5 мм. Если необходимо произвести измерения с большой точностью, пользуются приборами, снабженными нониусами. Нониусом называется дополнительная шкала к обычному масштабу, позволяющая повысить точность измерений в 10-20 раз. Линейный нониус представляет собой небольшую шкалу, скользящую вдоль основной шкалы. Деления на нониусе наносятся так, чтобы длина m делений нониуса была равна длине m-1 делений основной шкалы. Если число делений нониусной шкалы m, а цена деления основной шкалы y, тогда xm=(m-1)y, (1) где x– цена деления нониуса. Величина, определяемая разностью: y – x= 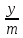 (2)называется точностью нониуса. Точность нониуса равна отношению цены деления основной шкалы к числу делений нониуса. Она определяет максимальную погрешность нониуса. При достаточно мелких делениях основной шкалы (масштаба) деления нониуса делают более крупными, например:  (3)Штангенциркуль служит для линейных измерений, не требующих высокой точности, и состоит из линейки с миллиметровым делением, вдоль которой может перемещаться подвижная рамка. На подвижной рамке нанесен линейный нониус с числом делений m. При измерении предмет зажимается между губками с помощью подвижной рамки. Микрометр. Для более точных измерений применяют микрометрические винты с малым и очень точно выдержанным шагом. Такие винты применяются в микрометрах, измерительных микроскопах и т.д. Микрометр имеет вид тисков, в которых измеряемый предмет зажимается с помощью винта. На стержне винта укреплен барабан с нанесенной на нем шкалой. Измерения:
Обработка результатов измерений:  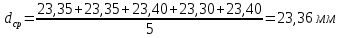 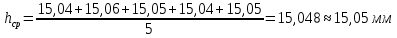 Δ D = Dср – D; Δ d = dср – d; Δ h = hср – h. Вычислим среднеквадратичные погрешности отдельных измерений, мм: 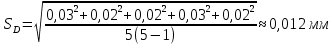 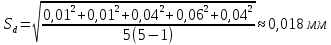 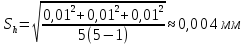 Принимаем значение надёжности Р = 0,95 и коэффициент Стьюдента для пяти измерений 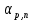 = 2,8.Вычислим случайные погрешности, мм: ΔD= 2,8 * 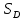 =0,033ммΔd=2,8 *  =0,050ммΔh=2,8*  =0,011ммПолная погрешность с учетом приборной, мм: ΔD= 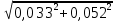 ≈0,059ммΔd=  ≈0,070ммΔh=  ≈0,014ммЗапишем результаты прямых измерений, мм: D=(63,42±0,059)мм; d=(23,36±0,070)мм; h=(15,05±0,014)мм Среднее значение объема кольца,  : Относительную погрешность объема вычислим по формуле:   Абсолютную погрешность измерения объема кольца, : 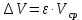;  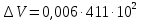; Записываем окончательный результат измерения объема, :V = (411 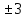 ) 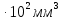, P = 0,95Вывод: Истинное значение объёма данного кольца с вероятностью 95% лежит в найденном интервале. Я ознакомился с основными положениями теории погрешностей, статистической обработкой результатов измерений, а также правилами и приемами измерений линейных и угловых величин, методом Стьюдента. Контрольные вопросы и задания 1. Что такое доверительный интервал и доверительная вероятность? Интервал значений от  до  , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностью измерений.2. Как находится абсолютная погрешность прямых измерений? Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:  3. Как вычислить абсолютные и относительные погрешности косвенных измерений? Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:  Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:  Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше. Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов. 4. Как оцениваются приборные погрешности? Инструментальная погрешность - определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.). Инструментальная погрешность измерений принимается равной половине цены деления прибора: 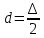 5. Чему равна погрешность табличных значений? Погрешность констант (табличных значений) равна половине их абсолютной погрешности. 6. Как устроен линейный нониус, где он применяется и чему равна его точность? Если измерение длины проводят с точностью до долей миллиметра, то пользуются вспомогательной шкалой измерительного инструмента – нониусом. Нониус бывает линейным – для измерения линейных величин и угловым – для измерения угловых величин. Линейный нониус (рис.1) представляет собой небольшую линейку С со шкалой, m делений которой равны m–1 делениям шкалы масштабной линейки А. Нониус С может перемещаться по линейке А. Если а – цена деления нониуса, b – цена деления масштабной линейки, m – число делений на нониусе, то связь между указанными делениями линейки и нониуса следующая: am=(m-1)b. 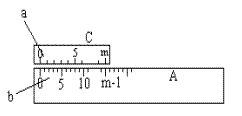 Получаемая из формулы разность   ,называется точностью нониуса, т.е. точность нониуса равна (b/m) –отношению цены наименьшего деления масштаба к числу делений на нониусе. Точность нониуса часто бывает равна 1/10 мм, в этом случае b=1мм, m=10. 7. Получить формулу относительной и абсолютной погрешности     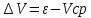  |