ИЗУЧЕНИЕ И ИССЛЕДОВАНИЕ ПРИНЦИПОВ ОБРАЗОВАНИЯ КОДОВ И КОДИРУЮЩИХ УСТРОЙСТВ. Лабораторная работа 1 изучение и исследование принципов образования кодов и кодирующих устройств Проверил
 Скачать 190.75 Kb.
|
|
Министерство образования Республики Беларусь Учреждение Образования БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра ПИКС Лабораторная работа № 1 «ИЗУЧЕНИЕ И ИССЛЕДОВАНИЕ ПРИНЦИПОВ ОБРАЗОВАНИЯ КОДОВ И КОДИРУЮЩИХ УСТРОЙСТВ» Проверил: Выполнил: Бересневич А.И. Бересневич А.И. Минск 2021 Цель работы: 1. Изучить базовые принципы кодирования, методы кодирования информации, простейшие варианты кодов. 2. Выполнить кодирование заданной последовательности цифр различными кодами. 3. Проанализировать целесообразность использования тех или иных кодов. 4. Сделать вывод о помехозащищенности кодов и простоте применения кодов и кодирующих устройств. Вариант задания: С помощью специальной программы были получены числа, показанные на рисунке 1. 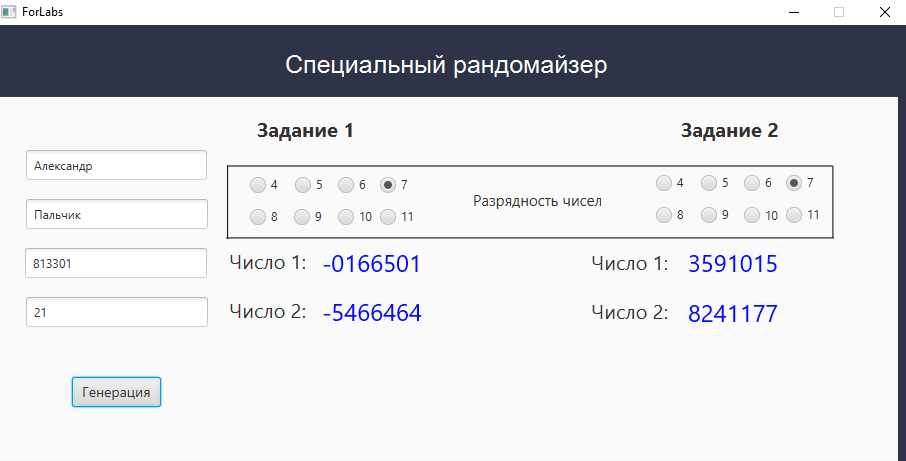 Рисунок 1 – Вариант задания Для задания 1 необходимо осуществить преобразование чисел следующими типами кодов: а) перевести последовательность в прямой код; Представим числа 0166501 и 5466464 в двоичном коде. 0166501(10) = 000000101000101001100101(2) 5466464(10) = 010100110110100101100000(2) Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1. Таким образом, число -0166501 в прямом двоичном коде записывается как 1,000000101000101001100101, а число -5466464 в прямом двоичном коде записывается как 1,010100110110100101100000. б) перевести в обратный код; Обратный код для положительных чисел совпадает с прямым кодом. Для отрицательных чисел все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица. Таким образом, число -0166501 имеет обратный код 1,111111010111010110011010, а число -5466464 в обратном двоичном коде записывается как 1,101011001001011010011111. в) перевести в дополнительный код; Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы. Число -0166501 в двоичном дополнительном коде будет 1,111111010111010110011011, а число -5466464 будет 1,101011001001011010100000. г) дополнительный код перекодировать в NRZ, NRZI; Для числа -0166501 код в NRZ (прямой) представлен на рисунке 2.  Рисунок 2 – код в NRZ (прямой) числа -0166501Для числа -5466464 код в NRZ (прямой) представлен на рисунке 3. 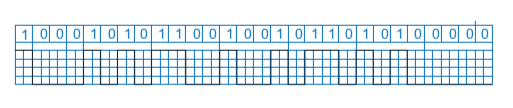 Рисунок 3 – код в NRZ (прямой) числа -5466464 Для числа -0166501 код в NRZ (перевёрнутый) представлен на рисунке 4.  Рисунок 4 – код в NRZ (перевёрнутый) числа -0166501Для числа -5466464 код в NRZ (перевёрнутый) представлен на рисунке 5. 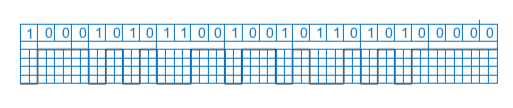 Рисунок 5 – код в NRZ (перевёрнутый) числа -5466464 Для числа -0166501 код в NRZI представлен на рисунке 6.  Рисунок 6 – код в NRZI числа -0166501Для числа -5466464 код в NRZI представлен на рисунке 7.  Рисунок 7 – код в NRZI числа -5466464 д) дополнительный код перекодировать в RZ; Для числа -0166501 код в RZ представлен на рисунке 8.  Рисунок 8 – код в RZ числа -0166501 Для числа -5466464 код в RZ представлен на рисунке 9.  Рисунок 9 – код в RZ числа -5466464 е) дополнительный код перекодировать методом Манчестерского кодирования, дифференциального манчестерского кодирования; Для числа -0166501 код методом Манчестерского кодирования представлен на рисунке 10.  Рисунок 10 – Манчестерское кодирование числа -0166501 Для числа -5466464 код методом Манчестерского кодирования представлен на рисунке 11.  Рисунок 11 – Манчестерское кодирование числа -5466464 Для числа -0166501 код методом дифференциального Манчестерского кодирования представлен на рисунке 12.  Рисунок 12 – дифференциальное Манчестерское кодирование числа -0166501 Для числа -5466464 код методом дифференциального Манчестерского кодирования представлен на рисунке 13.  Рисунок 13 – дифференциальное Манчестерское кодирование числа -5466464 ж) дополнительный код перекодировать в HDB3; Для числа -0166501 код в HDB3 представлен на рисунке 14.  Рисунок 14 – код в HDB3 числа -0166501 Для числа -5466464 код в HDB3 представлен на рисунке 15.  Рисунок 15 – код в HDB3 числа -5466464 з) дополнительный код перекодировать в АMI. Для числа -0166501 код в АMI представлен на рисунке 16.  Рисунок 16 – код в АMI числа -0166501 Для числа -5466464 код в АMI представлен на рисунке 17.  Рисунок 17 – код в АMI числа -5466464Выполнить арифметические действия сложения и вычитания для полученных кодов чисел в п.п. 4а, 4б, 4в. Так как числа -0166501 и -5466464 отрицательные, то необходимо перевести их в ДК(взять ОК и добавить единицу): Сложение числа 1 и числа 2: -0166501 + (-5466464) = 1000 0000 0010 1000 1010 0110 0101 = -0166501 ПК 1000 0101 0011 0110 1001 0110 0000 = -5466464 ПК Числа отрицательные – необходимо перевести в ДК 1111 1111 1101 0111 0101 1001 1011 = -0166501 ДК 1111 1010 1100 1001 0110 1010 0000 = -5466464 ДК Складываем два числа: 1111 1111 1101 0111 0101 1001 1011 + 1111 1010 1100 1001 0110 1010 0000 1111 1010 1010 0000 1100 0011 1011 Перенос из знакового разряда отбрасываем Инверсия: 1000 0101 0101 1111 0011 1100 0100 +1 1000 0101 0101 1111 0011 1100 0101 = -5632965 Результат: -0166501 + (-5466464) = -5632965 Вычитание числа 1 из числа 2: -5466464 + 0166501 = 0000 0000 0010 1000 1010 0110 0101 = 0166501 ПК 1000 0101 0011 0110 1001 0110 0000 = -5466464 ПК Число отрицательное – необходимо перевести в ДК 1111 1010 1100 1001 0110 1010 0000 = -5466464 ДК Складываем два числа: 0000 0000 0010 1000 1010 0110 0101 + 1111 1010 1100 1001 0110 1010 0000 1111 1010 1111 0010 0001 0000 0101 Инверсия всех разрядов, кроме знакового 1000 0101 0000 1101 1110 1111 1010 +1 1000 0101 0000 1101 1110 1111 1011 = -5299963 Результат: -5466464 + 0166501 = -5299963 Вычитание числа 2 из числа 1: 5466464 - 0166501 = 1000 0000 0010 1000 1010 0110 0101 = -0166501 ПК 0000 0101 0011 0110 1001 0110 0000 = 5466464 ПК Число отрицательное – необходимо перевести в ДК 1111 1111 1101 0111 0101 1001 1011 = -0166501 ДК Складываем два числа: 0000 0101 0011 0110 1001 0110 0000 + 1111 1111 1101 0111 0101 1001 1011 0000 0101 0000 1101 1110 1111 1011 Перенос из знакового разряда отбрасываем Число является положительным в ПК 0000 0101 0000 1101 1110 1111 1011 = 5299963 Результат: 5466464 - 0166501 = 5299963 Ход работы для задания 2 В таблице 1 показан перевод десятичных цифр с помощью кода Айкена (2-4-2-1) и кода с избытком 3 (8-4-2-1). Число 1: 3591015(10) = 0011 0110 1100 1011 0110 0111(2); Число 2: 8241177(10) = 0111 1101 1100 0000 0001 1001(2). Таблица 1 – Перевод десятичных цифр с помощью кода Айкена (2-4-2‑1) и кода с избытком 3 (8-4-2-1)
Кодирование с помощью кода Айкена (код 2-4-2-1): Число 1: 3591015(10) = 0011 1011 1111 0001 0000 0001 1011(2-4-2-1); Число 2: 8241177(10) = 1110 0010 0100 0001 0001 1101 1101(2-4-2-1). Кодирование с помощью кода с избытком 3 (код 8-4-2-1): Число 1: 3591015(10) = 0110 1000 1100 0100 0011 0100 1000(8-4-2-1 + 3); Число 2: 8241177(10) = 1011 0101 0111 0100 0100 1010 1010(8-4-2-1 + 3). Вывод: В ходе лабораторной работы были изучены базовые принципы кодирования, методы кодирования информации, простейшие варианты кодов. Выполнили кодирование заданной последовательности цифр (число 1: ‑9877417; число 2: -2349252) различными кодами (ПК, ОК, ДК, NRZ, NRZI, RZ, метод Манчестерского кодирования, метод дифференциального Манчестерского кодирования, HDB3, AMI). Прямой код (ПК) достаточно удобен, так как позволяет определить знак двоичного числа с помощью бита знака (если бит знака равен 0, то двоичное число положительное, если бит знака равен 1, то двоичное число отрицательное). На мой взгляд, HDB3 кодирование является самым сложным и неудобным, другие же методики кодирования примерно одинаково эффективны. При помехоустойчивом кодировании в поток передаваемых символов вводятся дополнительные (избыточные) символы для исправления возникающих на приемной стороне ошибок. Это требует увеличения скорости передачи по каналу, что при выбранном типе модема эквивалентно расширению полосы частот сигнала и уменьшению энергии посылки. Поэтому следует ожидать повышения достоверности передачи при заданной скорости и отношении сигнал/шум в канале при внесении избыточности. Кодирующим устройствам достаточно просто применять ПК, ОК, ДК, NRZ-, NRZI-, RZ-коды и метод Манчестерского кодирования, однако метод дифференциального Манчестерского кодирования, HDB3- и AMI-коды применять гораздо сложнее, так как они используют большее количество ресурсов для кодирования чисел, текста и др. |