Лабораторная работа 1 Математическое моделирование. Лабораторная работа 1 Линейное программирование. Симплексметод Вариант 11 Преподаватель Коннова Н. С
 Скачать 34.27 Kb. Скачать 34.27 Kb.
|
|
Министерство образования Российской Федерации МОСКВОСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Н.Э.БАУМАНА Факультет: Информатика и системы управления (ИУ) Кафедра: Информационная безопасность (ИУ8) МЕТОДЫ ОПТИМИЗАЦИИЛабораторная работа №1: «Линейное программирование. Симплекс-метод» Вариант – 11 Преподаватель: Коннова Н.С. Студент: Киселев В.А. Группа: ИУ8-34 Москва, 2021 Цель работыИзучить постановку задачи линейного программирования (ЛП); овладеть навыками решения задач ЛП с помощью симплекс-метода. Постановка задачиТребуется найти решение следующей задачи линейного программирования (ЛП): F = cx → max, Ax ≤ b, x ≥ 0. Здесь x = [x1, x2, …, xn]T – искомый вектор решения; c = [c1, c2, …, cn] – вектор коэффициентов целевой функции (ЦФ) F; [𝑎₁₁ ⋯ 𝑎₁ₙ 𝐀 = … … … - матрица системы ограничений 𝑎ₘ₁ ⋯ 𝑎ₘₙ] b = [b1, b2, …, bn]T – вектор правой части системы ограничений Задачу ЛП требуется записать в канонической форме. Затем следует решить задачу ЛП симплекс-методом, продемонстрировав на каждом этапе все преобразования симплекс-таблиц. Получив оптимальное решение, необходимо выполнить его проверку подстановкой. Ход работыДаны матрицы: c = [5 3 8]; [[2 1 1] A = [1 1 0] [0 0,5 2]] b = [3 6 3]; Решим следующую задачу ЛП: F = 5x1 + 3x2 + 8x3 → max 2𝑥₁ + 𝑥₂ + 𝑥₃ ≤ 3 𝑥₁ + 𝑥₂ ≤ 6 0,5𝑥₂ + 2𝑥₃ ≤ 3 x1, x2, x3 ≥ 0 Приведем к каноническому виду F = 5x1 + 3x2 + 8x3 → max: F = -5x1 - 3x2 - 8x3 → min 2𝑥₁ + 𝑥₂ + 𝑥₃ + 𝑥₄ = 3 𝑥₁ + 𝑥₂ + 𝑥₅ = 6 0,5𝑥₂ + 2𝑥₃ + 𝑥₆ = 3 x1, x2, x3, x4, x5, x6 ≥ 0 Пусть x4, x5, x6 – базисные переменные, x1, x2, x3 – свободные переменные. Тогда имеем F = -(2x1 + 5x2 + 3x3) → min 𝑥₄ = 6 − (2𝑥₁ + 𝑥₂ + 𝑥₃) 𝑥₅ = 6 − (𝑥₁ + 2𝑥₂) 𝑥₆ = 2 − (0,5𝑥₂ + 2𝑥₃) x1, x2, x3, x4, x5, x6 ≥ 0 Исходная симплекс-таблица:
Все элементы столбца si0 неотрицательны поэтому имеем опорное решение: x1=x2=x3= 0, x4= 3, x5= 6, x6= 3 Целевая функция F = 0 Разрешающий столбец – x3, разрешающая строка – x6. Изменим базис, поменяв местами переменные x3 и x6. Получим преобразованную симплекстаблицу:
Разрешающий столбец – x1, разрешающая строка – x4. Изменим базис, поменяв местами переменные x1 и x4. Получим преобразованную симплекстаблицу:
В строке F больше нет положительных коэффициентов, значит оптимальное решение найдено: x1 = 0.75, x2 =0 , x3 =1.5 Целевая функция: F = -(-15.75) = 15.75 Выполним проверку решения подстановкой: 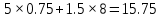 ВыводыВ ходе проделанной работы был изучен симплекс-метод решения задач линейного программирования. Мы научились приводить задачу к каноническому виду, искать опорное решение и оптимальное решение. При проверке значение целевой функции совпало. Приложение_А'>Приложение А Файл “Simple.h” #pragma once #include #include #include #include #include #include #include "nlohmann/json.hpp" class Simplex { int sizex, sizey, sizec, sizea; std::vector std::vector std::vector double funcMax; std::vector std::vector bool canSolve; bool infinite; Simplex(); bool optimal(); int findRow(); int findColumn(); void doTransform(int row, int col); void endless (int column); public: Simplex(std::vector void calculate(); void print(); void print2(); }; Приложение B Файл “Simple.cpp” #include "simplex.h" template std::string toString (const T val) { std::stringstream ss; ss << val; return ss.str(); } void swap(std::string &a, std::string &b) { std::string c = b; b = a; a = c; } Simplex::Simplex() {} Simplex::Simplex(std::vector { sizey = a.size(); sizea = a[0].size(); sizex = sizea + sizey; sizec = c.size() + sizey; funcMax = 0; canSolve = true; infinite = false; A.resize(sizey, std::vector B.resize(b.size()); C.resize(sizec); for (int i = 0; i < sizey; i++) for(int j = 0; j < sizea; j++) A[i][j] = a[i][j]; for (int i = 0; i < sizey; i++) for(int j = sizea; j < sizex; j++) { if (i == j - sizea) A[i][j] = 1; else A[i][j] = 0.0; } for (int i = 0; i < b.size(); i++) B[i] =b[i]; for (int i = 0; i < c.size(); i++) { //C[i] = -1 * c[i]; C[i] = c[i]; } titleCol.resize(sizey); titleRow.resize(sizex); for (int i = 0; i < sizey; i++) titleCol[i] = 'x' + toString(i + sizea + 1); for (int i = 0; i < sizex; i++) titleRow[i]='x'+ toString(i+1); } void Simplex::print() { std::cout << std::fixed << std::setprecision(3) << "B = {"; for (int i = 0 ; i < B.size(); i++) { std::cout << B[i]; if (i != B.size()-1) std::cout << ", "; } std::cout << "}\n"; std::cout << "C = {"; for (int i = 0 ; i < C.size(); i++) { std::cout << C[i]; if (i != C.size()-1) std::cout << ", "; } std::cout << "}\n"; std::cout << "A = {\n"; for (int i = 0 ; i < sizey; i++) { std::cout << " {"; for (int j = 0; j < sizex; j++) { std::cout << A[i][j]; if (j != sizex-1) std::cout << ", "; } std::cout << "}"; if (i != sizey-1) { std::cout << ",\n"; } } std::cout << "\n}\n***************************************************************************\n"; } bool Simplex::optimal() { for (int i = 0; i < C.size(); i++) if (C[i] > 0) { return false; } return true; } int Simplex::findColumn() { double max = 0; int index = 0; for (int i = 0; i < C.size(); i++) if (C[i] > max) { max = C[i]; index = i; } return index; } void Simplex::endless (int column) { int Count = 0; for (int i = 0 ; i < B.size(); i++) { if (A[i][column] < 0) Count++; } if (Count == B.size()) { infinite = true; } } int Simplex::findRow() { int index = 0; int col = findColumn(); double min = B[index] / A[index][col]; int Count = 0; for (int j = 0; j < B.size(); j++) { for (int i = 0; i < B.size (); i++) { if (A[j][i] >= 0 && B[j] < 0) Count++; } } if (Count == B.size()) { canSolve = false; } for (int i = 1; i < B.size(); i++) { if (B[i] / A[i][col] < min) { min = B[i] / A[i][col]; index = i; } } return index; } void Simplex::doTransform(int row, int col) { double elem = A[row][col]; std::vector std::vector std::vector std::vector funcMax = funcMax - (C[col]*(B[row]/elem)) ; for (int i = 0; i < sizex; i++) oldRow[i]=A[row][i]; for (int i = 0; i < sizey; i++) oldCol[i]=A[i][col]; for (int i = 0; i < sizex; i++) newRow[i] = oldRow[i]/elem; for (int i = 0; i < sizey; i++) newCol[i] = -1 * oldCol[i]/elem; for (int i = 0; i < sizey; i++) for(int j = 0; j < sizex; j++) A[i][j] = A[i][j] - oldCol[i]/elem * oldRow[j] + 0.0; for (int i = 0; i < sizey; i++) A[i][col] = newCol[i] + 0.0; for (int i = 0; i < sizex; i++) A[row][i] = newRow[i] + 0.0; B[row]=B[row]/elem + 0.0; for (int i = 0; i < sizey; i++) if (i!=row) B[i]= B[i] - oldCol[i]* B[row] + 0.0; for (int i = 0; i < sizex; i++) if (i!=col) C[i]=C[i]-C[col]/elem*oldRow[i] + 0.0; C[col] = -1 * C[col]/elem + 0.0; swap(titleCol[col], titleRow[row]); } void Simplex::calculate() { int step = 0; while ( !optimal() && canSolve) { endless(findColumn()); if (infinite) break; step++; print2(); doTransform(findRow(), findColumn()); } if (canSolve && !infinite) { std::cout << "Function maximum value: " << -funcMax << "\n"; print2(); for (int i = 0; i < sizey; i++) { for (int j = 0; j < sizey; j++) { if (titleCol[i] == 'x' + toString(j + 1)) { std::cout << " X" << toString(i + 1) << " = " << B[i] << " "; break; } else if (j == sizey - 1) { std::cout << " X" << toString(j) << " = 0"; } } } } else if (infinite) { std::cerr << "Function has infinite number of solutions" << "\n"; } else { std::cerr << "Can't solve..."; } } void Simplex::print2() { std::cout << std::fixed << std::setprecision(3) << " \t S0\t"; for (int i = 0; i < sizex-sizea; i++) { std::cout << " " << titleRow[i] << "\t"; } std::cout << "\n"; for (int i = 0; i < sizey; i++) { std::cout << titleCol [i] << "\t"; B[i] < 0 ? std::cout << B[i]: std::cout << " " << B[i]; std::cout << "\t"; for (int j = 0; j < sizex-sizea; j++) { A[i][j] < 0 ? std::cout << A[i][j] << "\t" : std::cout << " " << A[i][j] << "\t" ; } std::cout << "\n"; } std::cout <<"F\t"; funcMax < 0 ? std::cout << funcMax : std::cout << " " << funcMax; std::cout << "\t"; for (int i = 0; i < sizex-sizea; i++) { C[i] < 0 ? std::cout << C[i] << "\t" : std::cout << " " << C[i] << "\t" ; } std::cout << "\n\n***************************************************************************\n"; } Приложение C Файл “main.cpp” #include #include "simplex.h" #include "nlohmann/json.hpp" using json = nlohmann::json; int main(int argc, char * argv[]) { if (argc < 2) { throw std::runtime_error ("Path is required as parameter!"); } std::string jsonPath = argv[1]; std::ifstream file{jsonPath}; if (!file) { throw std::runtime_error{"unable to open json: " + jsonPath}; } json data; try { file >> data; } catch (std::exception & e) { throw std::runtime_error{"Wrong json format"}; } std::vector std::vector std::vector if (data.at("C").is_array()) { c = data.at("C").get b = data.at("B").get a = data.at("A").get } Simplex s (a, b, c); s.calculate(); return 0; } |
