Лаба Методы экспертных оценок. лаба 1. Лабораторная работа 1 Методы экспертных оценок Выполнил студент группы Принял Громов С. В. Москва 2020 Задание
 Скачать 138.33 Kb. Скачать 138.33 Kb.
|
|
Министерство образования и науки РФ Федеральное государственное автономное образовательное учреждение «Национальный исследовательский технологический университет «МИСиС» Институт ИТАСУ Каф. АСУ Лабораторная работа № 1 «Методы экспертных оценок» Выполнил студент группы Принял: Громов С. В. Москва 2020 Задание Эксперты провели оценку шести альтернатив, используя собственные шкалы в баллах.
Определить групповую экспертную оценку каждой альтернативы. Теоретическая часть Групповая экспертная оценка Пусть 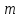 экспертов произвели оценку экспертов произвели оценку 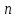 альтернатив по альтернатив по  показателям. Результаты оценки представим в виде величин показателям. Результаты оценки представим в виде величин 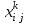 , где , где 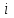 – номер эксперта ( – номер эксперта ( ), ),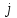 – номер альтернативы ( – номер альтернативы (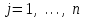 ), ), 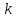 – номер показателя (признака) сравнения. Если оценка альтернатив произведена методом ранжирования, то величины – номер показателя (признака) сравнения. Если оценка альтернатив произведена методом ранжирования, то величины 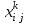 представляют собой ранги. Если оценка альтернатив выполнена методом непосредственной оценки, то величины представляют собой ранги. Если оценка альтернатив выполнена методом непосредственной оценки, то величины 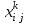 представляют собой числа из некоторого отрезка числовой оси или баллы. представляют собой числа из некоторого отрезка числовой оси или баллы.Рассмотрим случай, когда величины 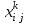 являются числами или баллами. Для получения групповой оценки альтернатив в этом случае можно воспользоваться средним значением оценки каждого объекта: являются числами или баллами. Для получения групповой оценки альтернатив в этом случае можно воспользоваться средним значением оценки каждого объекта: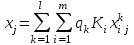 , , 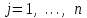 , ,где 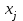 – групповая оценка – групповая оценка 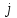 -й альтернативы, -й альтернативы, 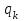 – коэффициенты весов показателей сравнения альтернатив; – коэффициенты весов показателей сравнения альтернатив;  – коэффициенты компетентности экспертов. – коэффициенты компетентности экспертов.Обычно используют нормированные коэффициенты весов показателей и компетентности экспертов:  , , 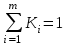 . .Коэффициенты весов показателей могут быть определены экспертным путем. Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, т. е. по результатам оценки альтернатив. Основной идеей этого вычисления является предположение о том, что компетентность экспертов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов. Пусть 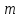 экспертов оценили экспертов оценили 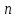 альтернатив, используя одну и ту же шкалу интервалов. Тогда мы имеем матрицу оценок альтернатив, используя одну и ту же шкалу интервалов. Тогда мы имеем матрицу оценок 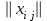 , , 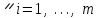 , , 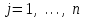 , где , где 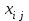 – оценка – оценка 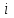 -го эксперта для -го эксперта для 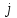 -го объекта. -го объекта.Алгоритм 2.1 (Евланова Л.Г. и Кутузова В.А.), основан на итеративной процедуре корректировки коэффициентов компетентности 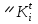 , ,  , , 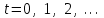 – номер итерации. – номер итерации.Алгоритм 2.1  , начальные значения коэффициентов компетентности , начальные значения коэффициентов компетентности  , ,  . .Затем на шагах 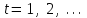 коэффициенты компетентности корректируются по формулам: коэффициенты компетентности корректируются по формулам: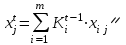 , ,  , , 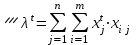 , , 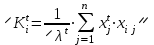 , , 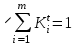 . .Коэффициент конкордации Кендалла Оценка согласованности мнений экспертов, когда число экспертов больше двух. Пусть 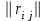 – матрица результатов ранжировки, полученной в результате оценки – матрица результатов ранжировки, полученной в результате оценки 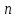 альтернатив альтернатив 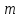 экспертами, т. е. экспертами, т. е. 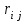 – ранг, присваемый – ранг, присваемый 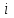 -м экспертом -м экспертом 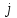 -й альтернативе. -й альтернативе.Составим суммы рангов по каждому столбцу. В результате получим вектор с компонентами: 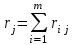 , , 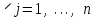 . .Величины 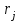 рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой: рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой: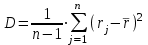 , ,где 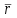 – оценка математического ожидания, равная – оценка математического ожидания, равная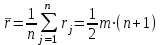 . .Дисперсионный коэффициент конкордации определяется как отношение оценки дисперсии к максимальному значению этой оценки: 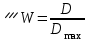 , (2.9) , (2.9)где 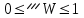 , так как , так как 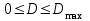 . .Для случая отсутствия связанных рангов (все альтернативы разные) дисперсионный коэффициент конкордации определяется по формуле Кендалла: 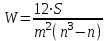 , , 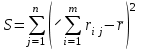 . (2.10) . (2.10)При наличии связанных рангов дисперсионный коэффициент конкордации вычисляется по следующей формуле:  , ,  (2.11) (2.11)где  – показатель связанных рангов в – показатель связанных рангов в 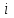 -й ранжировке; -й ранжировке; 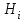 – число групп равных рангов в – число групп равных рангов в 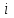 -й ранжировке; -й ранжировке;  – число равных рангов в – число равных рангов в 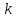 -й группе связанных рангов в -й группе связанных рангов в 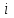 -й ранжировке. -й ранжировке.Если совпадающих рангов нет, то 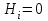 , , 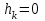 и, следовательно, и, следовательно, 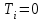 . В этом случае формула (2.11) совпадает с формулой (2.10). . В этом случае формула (2.11) совпадает с формулой (2.10).Коэффициент конкордации 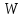 равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т. е. совершенно нет совпадения. равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т. е. совершенно нет совпадения.Расчетная часть Групповая экспертная оценка
Находим максимум у каждого эксперта. Так максимумы разные, то шкалы тоже могут быть разные, тогда проводим нормализацию оценок экспертов (разделяем оценки на идеальную). Тогда получаем:
 , начальные значения коэффициентов компетентности , начальные значения коэффициентов компетентности  , ,  . Затем на шагах . Затем на шагах 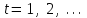 коэффициенты компетентности корректируются по формулам: коэффициенты компетентности корректируются по формулам: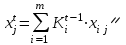 , ,  , , 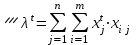 , , 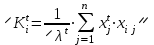 , , 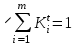 , получаем: , получаем:
Рассчитаем разницу значений при t=0 и t=1
Так как разница очень мала, то можно остановиться. Коэффициент конкордации Кендалла Матрица результатов ранжировки и суммы рангов по каждому столбцу. В результате получим вектор с компонентами: 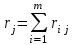 , , 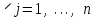 . .
Оценка математического ожидания равна: 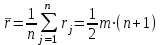 = =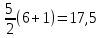 Оценка дисперсии: 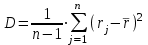 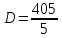 = 81 = 81Дисперсионный коэффициент конкордации по формуле Кендалла 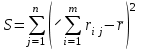 = 405 = 405У нас имеютя связанные ранги, поэтому дисперсионный коэффициент конкордации вычисляется по следующей формуле:  , ,  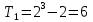 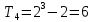 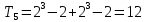 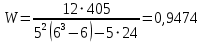 Используем таблицу 7П (т.к. 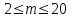 , ,  ), при входных данных n=6 и m=5, тогда ), при входных данных n=6 и m=5, тогда 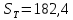 . . Следовательно,  , поэтому следует отвергать гипотезу об отсутствии связей между ранжировками (признавать их статистическую значимость). , поэтому следует отвергать гипотезу об отсутствии связей между ранжировками (признавать их статистическую значимость).Вывод В результате выполнения лабораторной работы мы научились использовать метод экспертных оценок для решения сложных проблем. Так же была доказана статистическая значимость и ,в результате обработки, было получено обобщенное мнение экспертов, которое считается решением проблемы. Список литературы Методы экспертных оценок. Теория и практика. (Гуцыкова Светлана) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
