Лабора. Лабораторная работа 1 Моделирование на эвм дискретных и квантованных сигналов
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
2.Что называется спектром детерминированного сигнала? 3.Какие базисные функции называются ортогональными, ортонормированными? 4.Что называется нормой базисной функции и чему она равна для тригонометрических функций? 5.Как выглядят спектры для одного и того же сигнала по системе экспоненциальных и тригонометрических функций? 6.Назовите физический смысл спектральной плотности для непериодического сигнала? 7.В чем заключается идея БПФ и какой частоте кратны гармоники спектра, полученного с помощью БПФ? 8.Что понимается под энергетическим спектром случайного сигнала и как он связан корреляционной функцией? 6. Литература. 1. Гоноровский И.С. " Радиотехнические цепи и сигналы" . 2. Конспект лекций по курсу "Теоретические основы информационной техники". 3. Баскаков С.И. " Радиотехнические цепи и сигналы". Лабораторная работа № 3 рекурсивный цифровой фильтр Цель работы. Целью настоящей работы является исследование алгоритмов работы простейших рекурсивных цифровых фильтров, а также расчет их АЧХ и ФЧХ. В работе исследуются рекурсивные цифровые фильтры первого и второго порядков. 2. Краткие теоретические сведения. В настоящее время широко используются методы обработки радиотехнических сигналов с помощью микроэлектронных вычислительных устройств и систем. Рассмотрим простейший, наиболее изученный и внедренный класс систем дискретной обработки сигналов — так называемые линейные стационарные цифровые фильтры. Выполняя, подобно аналоговым цепям, операцию частотной фильтрации, цифровые фильтры (ЦФ) обладают рядом существенных преимуществ. Сюда относятся, например, высокая стабильность параметров, возможность получать самые разнообразные формы АЧХ и ФЧХ. Цифровые фильтры не требуют настройки и легко реализуются на ЭВМ программными методами. На рис. 3.1 приведена основная структурная схема цифровой обработки сигналов. 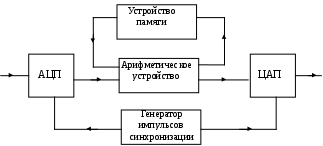 Рис.3.1. Структурная схема цифровой обработки непрерывных сигналов Непрерывный входной сигнал x(t) поступает в аналогово-цифровой преобразователь (АЦП), управляемый синхронизирующими импульсами от генератора, задающего частоту дискретизации. В момент подачи синхронизирующего импульса на выходе АЦП возникает сигнал, отображающий результат измерения мгновенного значения входного колебания в виде двоичного числа с фиксированным количеством разрядов. В зависимости от особенности построения устройства этому числу соответствует либо последовательность коротких импульсов (передача в последовательном коде), либо совокупность уровней напряжений на сигнальных шинах отдельных разрядов (передача в параллельном коде). Преобразованный таким образом сигнал поступает в основной блок устройства, так называемый цифровой процессор, состоящий из арифметического устройства и устройства памяти. Арифметическое устройство выполняет над цифрами ряд операций, таких, как умножение, сложение и сдвиг во времени на заданное число интервалов дискретизации. В устройстве памяти может храниться некоторое число предшествующих отсчетов входного и выходного сигналов, которые необходимы для выполнения операций обработки. Цифровой процессор преобразует поступающие в него числа в соответствии с заданным алгоритмом фильтрации и создает на выходе последовательность двоичных чисел, представляющих выходной сигнал. Если в дальнейшем необходимо иметь информацию в аналоговой форме, то используется цифро-аналоговый преобразователь (ЦАП). Однако это устройство может и отсутствовать, если сигналы подвергаются только цифровым преобразованиям. Специфика любого цифрового устройства — представление сигналов в виде последовательности чисел с ограниченной разрядностью. Поэтому мгновенное значение сигнала дискретизируется по уровню таким образом, что интервалом дискретизации (минимальной разностью между двумя соседними уровнями) служит единица младшего двоичного разряда. Математическая теория цифровых фильтров переносит на случай дискретных сигналов все основные положения теории линейных систем, преобразующих непрерывные сигналы. Как известно, линейная стационарная система преобразует непрерывный входной сигнал x(t) таким образом, что на ее выходе возникает колебание y(t), равное свертке функции x(t) и импульсной характеристики h(t): Линейный цифровой фильтр, по определению, есть дискретная система (физическое устройство или программа для компьютера), которая преобразует последовательность {xk} числовых отсчетов входного сигнала в последовательность {уk} отсчетов выходного сигнала. Для того чтобы обобщить формулу (15.45) на случай дискретных сигналов, вводят понятие импульсной характеристики ЦФ. По определению, она представляет собой дискретный сигнал {hk}, который является реакцией ЦФ на «единичный импульс» (1, 0, 0, 0, ...): Рассмотрим общий алгоритм линейной цифровой фильтрации. Пусть {хк} = (х0, х1 х2, ...) —некоторый сигнал на входе ЦФ с известной импульсной характеристикой. Можно записать m-й отсчет выходного сигнала {ук}: Формула (3.3), играющая ведущую роль в теории линейной цифровой фильтрации, показывает, что выходная последовательность есть дискретная свертка входного сигнала и импульсной характеристики фильтра. Смысл этой формулы прост и нагляден: в момент каждого отсчета ЦФ проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала, причем роль последовательности весовых коэффициентов играют отсчеты импульсной характеристики. Иными словами, ЦФ обладает некоторой «памятью» по отношению к прошлым входным воздействиям. Физически осуществимые ЦФ, которые работают в реальном масштабе времени, для формирования выходного сигнала в i-й дискретный момент времени могут использовать следующие данные: а) значение входного сигнала в момент i-го отсчета, а также некоторое число «прошлых» входных отсчетов xi-1, xi-2, … xi-m ; б) некоторое число предшествующих отсчетов выходного сигнала yi-1, yi-2, … yi-n .Целые числа m и n определяют порядок ЦФ. Классификация ЦФ проводится по-разному в зависимости от того, как используется информация о прошлых состояниях системы. Алгоритм работы линейного цифрового фильтра имеет в общем случае следующий вид: где a0, a1, ..., am, b1, b2, ..., bn последовательность коэффициентов; у(к) - выходной сигнал фильтра. Если все коэффициенты bi равны нулю, то фильтр называется трансверсальным и не имеет обратных связей. Если bi не равны нулю все одновременно, то фильтр называется рекурсивным. Алгоритм функционирования трансверсального ЦФ поясняется структурной схемой, приведенной на рис.3.1. 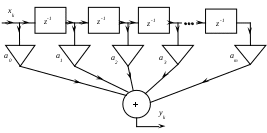 Рис.3.1. Структурная схема трансверсального цифрового фильтра. Основными элементами фильтра служат блоки задержки отсчетных значений на один интервал дискретизации (прямоугольники с символами z-1), а также масштабные блоки, выполняющие в цифровой форме операции умножения на соответствующие коэффициенты. С выходов масштабных блоков сигналы поступают в сумматор, где, складываясь, образуют отсчет выходного сигнала. Вид представленной здесь схемы объясняет смысл термина «трансверсальный фильтр» (от англ. transverse — поперечный). Если взять z-преобразование от обеих частей выражения, описывающего алгоритм работы, то можно получить выражение для системной функции H(z) : 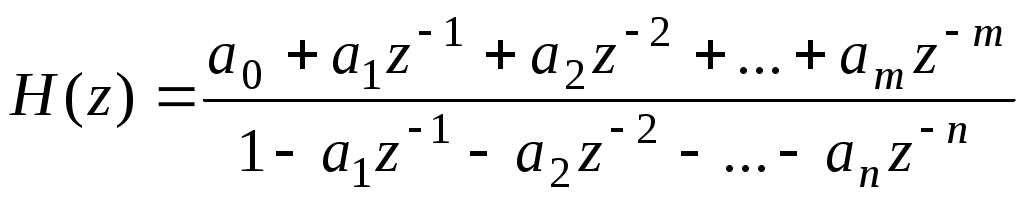 (3.5) (3.5)От системной функции легко перейти к частотному коэффициенту передачи K(j) фильтра путем замены в выражении для H(z) где Т шаг дискретизации сигнала по времени. Особенностью комплексного коэффициента передачи K(j) цифрового фильтра является то, что она является периодической функцией частоты с периодом, равным частоте дискретизации сигнала д : Изменяя коэффициенты a0, a1, ..., b1, b2, ... можно получить цифровые фильтры с различными амплитудно-частотными характеристиками. Построить амплитудно-частотную и фазо-частотную характеристики, зная комплексный коэффициент передачи, можно следующим образом: Трансверсальный фильтр первого порядка. Алгоритм работы этого фильтра в соответствии с (3.4) имеет вид Системная функция в этом случае равна а частотный коэффициент передачи равен где = jТ. Масштабный коэффициент а0 без ограничения общности можно положить равным единице. Фазо-частотная характеристика этого фильтра При a1 = 1 фильтр можно использовать для подавления колебаний с частотами, близкими к Т = , а при a1 = -1 - близкими к Т = 0 и 2. Подобные фильтры часто называют гребенчатыми режекторными фильтрами. Следует отметить, что при a1 = -1 фазо-частотная характеристика фильтра линейна Трансверсальный фильтр второго порядка. Алгоритм работы фильтра имеет вид Системная функция этого фильтра равна Положим a0 =1 .Тогда H(z) имеет нули в точках: Двухкратный полюс, расположенный в точке z = 0, не влияет на поведение системной функции на z-плоскости. Особый интерес представляет случай a2 = 1, │a1│< 2 . В этом случае модуль z1,2 равен единице, так что комплексно-сопряженные нули z1 и z2 лежат на окружности единичного радиуса. При a0 = a2 = 1 коэффициент передачи фильтра будет равен Изменением коэффициента a1 можно перемещать нули z1, z2 по окружности, что эквивалентно перемещению нулей на оси частот. Трансверсальные цифровые фильтры не являются динамическими системами, и устойчивы при любом выборе коэффициентов Рассмотренный фильтр можно рассматривать как режекторный фильтр второго порядка. Его можно реализовать также каскадным соединением двух фильтров первого порядка. ФЧХ этого фильтра линейна и может быть получена удвоением формулы (3.8). Рекурсивный фильтр. На рис. 3.2 изображена схема алгоритма вычислений, проводимых в соответствии с формулой (3.4). Верхняя часть структурной схемы отвечает трансверсальной (нерекурсивной) части алгоритма фильтрации. Для ее реализации требуется в общем случае m + 1 масштабных блоков (операций умножения) и m ячеек памяти, в которых хранятся входные отсчеты. Рекурсивной части алгоритма соответствует нижняя часть структурной схемы. Здесь используются n последовательных значений выходного сигнала, которые в процессе работы фильтра перемещаются из ячейки в ячейку путем сдвига.  Рис.3.2.Структурная схема рекурсивного цифрового фильтра Недостатком данного принципа реализации является потребность в большом числе ячеек памяти, отдельно для рекурсивной и нерекурсивной частей. Более совершенны канонические схемы рекурсивных ЦФ, в которых используется минимально возможное количество ячеек памяти, равное наибольшему из чисел m и n. В качестве примера на рис. 3.3 изображена структурная схема канонического рекурсивного фильтра 2-го порядка. 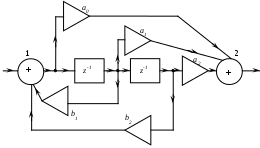 Рис.3.3. Структурная схема канонического рекурсивного ЦФ 2-го порядка Рекурсивный ЦФ является дискретным аналогом динамической системы с обратной связью, поскольку в ячейках памяти хранятся значения его предшествующих состояний. Если заданы некоторые начальные условия, т.е. совокупность значений yi-1, yi-2 ,…, yi-n, то в отсутствие входного сигнала фильтр будет образовывать элементы бесконечной последовательности yi , yi+1, yi+2, . . . , играющей роль свободных колебаний. Цифровой фильтр называется устойчивым, если возникающий в нем свободный процесс есть невозрастающая последовательность, т. е. значения ǀуnǀпри Если все полюсы системной функции H(z) т. е. числа z1 =α1 , z2 = α2 , …, zn = αn по модулю не превосходят единицы, располагаясь внутри единичного круга с центром в точке z = 0, то любой свободный процесс в ЦФ будет описываться членами убывающих геометрических прогрессий и фильтр будет устойчив. Ясно, что практически применяться могут только устойчивые цифровые фильтры. Характерная черта, отличающая рекурсивный ЦФ, состоит в том, что из-за наличия обратной связи его импульсная характеристика имеет вид неограниченно-протяженной последовательности. Рекурсивный фильтр первого порядка. Алгоритм работы этого фильтра имеет вид: При любом знаке b1 для устойчивой работы должно выполняться условие │b1│<1. Системная функция H(z) имеет один полюс в точке z1= b1. АЧХ фильтра сильно зависит от знака весового коэффициента b1, с приближением │b1│к единице полоса прозрачности фильтра уменьшается, а усиление резко возрастает. Интересно отметить, что системная функция этого фильтра совпадает с z - преобразованием от отсчетов, взятых через интервал Т из экспоненты Таким образом, импульсная характеристика рассматриваемого фильтра совпадает с последовательностью отсчетов из импульсной характеристики аналоговой цепи (например, RC-цепи), постоянная времени которой 1/ = RC отвечает условию 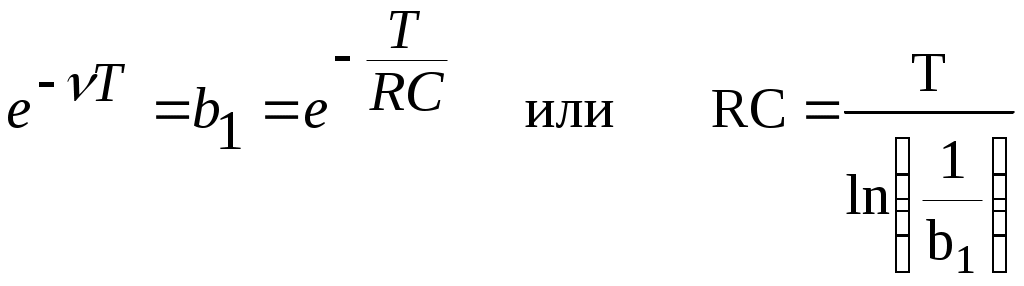 . .АЧХ цепей при этом на участке 0 < T < (RC >> T ) почти совпадают, а при T > существенно различны. Рекурсивный фильтр второго порядка Алгоритм работы этого фильтра записывается в виде Рассмотрим случай, когда а0 = 1, а1 = 0, а2 = 0. Тогда системная функция H(z) будет Нули этой функции имеются только в точке z = 0 , т.е. в центре окружности единичного радиуса. Полюсы равны При b2<0 и │b2│> (b12/4) полюса являются комплексно-сопряженными числами В этом случае откуда вытекают следующие соотношения Представив zп1,п2 в форме Для частного случая пТ=/2 частотный коэффициент передачи приводится к виду С приближением r к единице рассматриваемый фильтр приближается к резонатору с высокой добротностью. 3. Порядок выполнения работы 1. Исследовать рекурсивный фильтр первого порядка, алгоритм работы которого в общем виде имеет вид 2. Вычислить и вывести на экран графики АЧХ этого фильтра при b1=0,83 и при b1= -0,83 (объяснить, почему для устойчивости фильтра должно выполняться условие │b1│< 1). 3. Сравнить АЧХ этого фильтра с АЧХ аналоговой цепи, имеющей 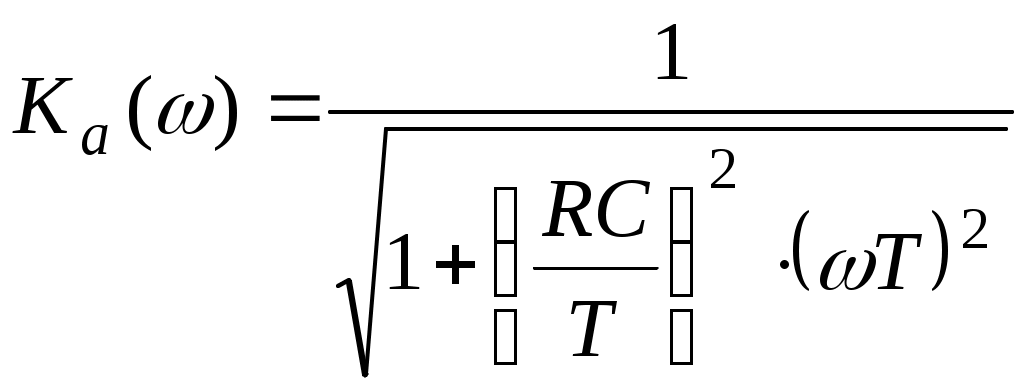 , ,для RC/T =5 (что соответствует b1= 0,83). 4. Исследовать рекурсивный фильтр второго порядка, алгоритм работы которого в общем виде имеет вид где а1=а2=0 , а0=1. Коэффициенты b1, b2 связаны с полюсами системной функции выражениями где r расстояние полюса от начала координат, а п=пТ азимут полюса. 5. Вычислить и вывести на экран графики АЧХ фильтра для пТ=/2 и r=(0,75; 0,875; 0,9375). 6. Вычислить и вывести на экран АЧХ фильтра для а0=а2=1, а1= -2, b1=0,21875, b2= -0,4375. Содержание отчета Отчет должен содержать программы вычисления АЧХ фильтров и графики АЧХ и ФЧХ. Контрольные вопросы. |
