Лабора. Лабораторная работа 1 Моделирование на эвм дискретных и квантованных сигналов

• Название: Лабораторная работа 1 Моделирование на эвм дискретных и квантованных сигналов
• Анкор: Лабора
• Дата: 26.01.2023
• Размер: 0.78 Mb.
• Имя файла: Laboratornye.doc
• Тип: Лабораторная работа; #906452
• страница: 1 из 3

лабораторный практикум по курсу

«теоретические основы информационно-измерительной техники»

ЛАБОРАТОРНАЯ РАБОТА № 1
Моделирование на ЭВМ дискретных и квантованных сигналов.
1. Цель работы:
Ознакомление с пакетом прикладных программ MathCAD и моделирование основных дискретных испытательных сигналов.
2. Краткие теоретические сведения.
С информационной точки зрения сигналы можно разделить на детерминированные и случайные.

Детерминированным называют любой сигнал, мгновенное значение которого в любой момент времени можно предсказать с вероятностью единица. Примерами детерминированных сигналов могут служить импульсы или пачки импульсов, форма, амплитуда и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра.

К случайным относят сигналы, мгновенные значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Такими сигналами являются, например, электрическое напряжение, соответствующее речи, музыке, последовательности знаков телеграфного кода при передаче неповторяющегося текста. По существу, любой сигнал, несущий в себе информацию, должен рассматриваться как случайный.

Наряду с полезными случайными сигналами в теории и практике приходится иметь дело со случайными помехами — шумами.

Применяемые в современной радиоэлектронике сигналы можно разделить на следующие классы:

- произвольные по величине и непрерывные по времени (рис. 1.1, а);

- произвольные по величине и дискретные по времени (рис. 1.1, б);

- квантованные по величине и непрерывные по времени (рис. 1.1, в);

- квантованные по величине и дискретные по времени (рис. 1.1, г).

Сигналы первого класса (рис. 1.1, а) иногда называют аналоговыми, так как их можно толковать как электрические модели физических величин, или непрерывными, так как они задаются по оси времени на несчетном множестве точек. Такие множества называются континуальными. При этом по оси ординат сигналы могут принимать любое значение в определенном интервале. Поскольку эти сигналы могут иметь разрывы, как на рис. 1.1.а), то, чтобы избежать некорректности при описании, лучше такие сигналы обозначать термином континуальный.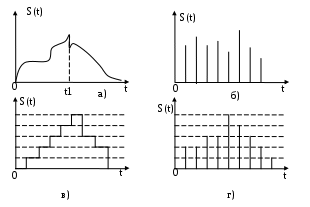


Рис.1.1. Сигналы произвольные по величине и по времени (а), произвольные по величине и дискретные по времени (б), квантованные по величине и непрерывные по времени (в), квантованные по величине и дискретные по времени (г).
Итак, аналоговый сигнал s(i) является функцией непрерывной переменной t, а дискретный сигнал s(x) — функцией дискретной переменной х, принимающей только фиксированные значения. Дискретные сигналы могут создаваться непосредственно источником информации (например, дискретными датчиками в системах управления или телеметрии) или образовываться в результате дискретизации континуальных сигналов.

На рис. 1.1, б) представлен сигнал, заданный при дискретных значениях времени t (на счетном множестве точек); величина же сигнала в этих точках может принимать любое значение в определенном интервале по оси ординат (как и на рис. 1.1, а). Таким образом, термин дискретный характеризует не сам сигнал, а способ задания его на временной оси.

Сигнал на рис. 1.1, в) задан на всей временной оси, однако его величина может принимать лишь дискретные значения. В подобных случаях говорят о сигнале, квантованном по уровню. В дальнейшем термин дискретный будет применяться только по отношению к дискретизации по времени; дискретность же по уровню будет обозначаться термином квантование.

Дискретные сигналы, уровни которых могут принимать лишь счетное множество значений, называют квантованными сигналами.

Квантование используют при представлении сигналов в цифровой форме с помощью цифрового кодирования, поскольку уровни можно пронумеровать числами с конечным числом .разрядов. Поэтому дискретный по времени и квантованный по уровню сигнал (рис. 1.1, г) называют цифровым.

Таким образом, можно различать континуальные (рис. 1.1, а), дискретные (рис. 1.1, б), квантованные (рис. 1.1, в) и цифровые (рис. 1.2, г) сигналы.
Итак, основное свойство дискретного сигнала: его значения определены не во все моменты времени, а лишь в счетном множестве точек. Если аналоговый сигнал имеет математическую модель вида непрерывной или кусочно-непрерывной функции, то отвечающий ему дискретный сигнал x_д(t) представляет собой последовательность (..., х_-1 , х₀ , х₁ , х₂, ...) отсчетных значений сигнала x(t) в точках (..., t_-1, t₀, t₁, t₂, ...) соответственно. На практике, как правило, отсчеты дискретных сигналов берут во времени через равный промежуток ∆t, называемый интервалом (шагом) дискретизации:

Шаг дискретизации должен удовлетворять теореме Котельникова.

Теорема Котельникова (теорема отсчетов) гласит:

если наивысшая частота в спектре функции s(t) меньше, чем f_max, то функция s(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/2f_max, секунд.

В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой , можно представить рядом



В этом выражении обозначает интервал между двумя отсчетными точками на оси времени, а s(n∆t) - выборки функции s(t) в моменты времени t=n∆t.

Таким образом, под дискретизацией сигнала s(t) подразумевается аналитическое его представление с помощью совокупности отсчетов в дискретные моменты времени, равные n∆t.

Введем понятие дельта-функции или функции Дирака.

Рассмотрим импульсный сигнал прямоугольной формы (см. рис.1.2), заданный следующим образом: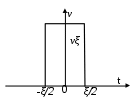





Рис.1.2 Импульс прямоугольной формы.
При любом выборе параметра ξ, площадь этого импульса равна единице:



Например, если v — напряжение, то П_v = 1 Вс. Пусть теперь величина ξ стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предел последовательности таких функций при носит название дельта-функции, или функции Дирака:

(1.1)

Будучи равной нулю всюду, за исключением точки t = 0 (принято говорить, что она сосредоточена в этой точке), дельта-функция обладает единичным интегралом: 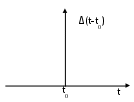. Символическое изображение дельта-функции приведено на рис.1.3.



Рис.1.3. Символическое изображение дельта-функции
Основная причина, делающая дельта-функцию столь удобной в физических задачах, состоит в следующем: дельта-функция является математической моделью короткого внешнего воздействия с единичным импульсом. При помощи дельта-функции можно дискретизировать непрерывный сигнал:

(1.4)

Важное свойство дельта-функции: ее физическая размерность такая же, как и размерность частоты, т. е. с^-1.

Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен δ-импульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.

Операцию дискретизации, т. е. переход от аналогового сигнала s(t) к дискретному сигналу s_д(t), можно описать, введя в рассмотрение обобщенную функцию называемую дискретизирующей последовательностью:

(1.5)

Очевидно, дискретный сигнал s_д(t) представляет собой функционал, определенный на множестве всевозможных аналоговых сигналов s(t) и равный скалярному произведению функции s(t) и η(t):

(1.6)

Формула (1.6) указывает путь реализации дискретизации аналогового сигнала. Дискретизация основана на операции стробирования — перемножения обрабатываемого сигнала s(t) и «гребенчатой» функции η(t). Поскольку длительность отдельных импульсов, из которых складывается дискретизирующая последовательность, равна нулю, на выходе идеального дискретизатора в равноотстоящие моменты времени возникают отсчетные значения обрабатываемого аналогового сигнала. Такой сигнал называется модулированной импульсной последовательностью (МИП). Естественно, что дискретный сигнал является математической моделью МИП. Такая математическая модель модулированной импульсной последовательности, образованной бесконечно короткими импульсами, окажется заданной выражением:

(1.7)

где — выборочные значения аналогового сигнала.

В данной лабораторной работе используются три испытательных сигнала, которые впоследствии будут подаваться на вход цифрового фильтра - это дискретный аналог меандра и дискретный аналог гармонического (синусоидального) сигнала, амплитуды которых равны 1, и случайный сигнал n(k), ограниченный по амплитуде в пределах -1≤ n(k) ≥1, где число k – это заданное число отсчетов

Меандр - это импульсный сигнал прямоугольной формы, представленный на рис 1.4.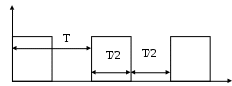



Рис 1.4. Прямоугольный импульсный сигнал, называемый меандром
Линейный цифровой фильтр, по определению, есть дискретная система (физическое устройство или программа для компьютера), которая преобразует последовательность {x_k} числовых отсчетов входного сигнала в последовательность {у_k} отсчетов выходного сигнала.

Как известно, в теории линейных систем особую роль играют комплексные сигналы вида , отображающие гармонические колебания. При дискретизации такого сигнала по времени получается так называемая гармоническая последовательность , такая, что:



При моделировании дискретной гармонической последовательности по аналоговому сигналу удобнее брать отсчеты не через временной шаг дискретизации  t, а через фазовый угол : .

Таким образом, если временной шаг дискретизации является константой для конкретного цифрового фильтра, то уменьшение угла –  эквивалентно уменьшению частоты аналогового сигнала s(t), из которого берутся отсчеты (и увеличению числа отсчетов за период). Такой подход дает возможность при анализе АЧХ цифровых фильтров не привязываться к тактовой частоте фильтра (шагу дискретизации) и вместо оси частот использовать ось  - фазового угла интервала дискретизации при текущем значении частоты. Одно и тоже значение угла  могут иметь фильтры с разным шагом дискретизации, но для разных частот .

Генератор случайных чисел пакета MathCAD генерирует числа с равномерным распределением от 0 до некоторого заданного числа a. Для получения симметричного распределения относительно нуля нужно сместить все выборки случайного сигнала на a/2 вниз.
3. Порядок выполнения работы.
1. Познакомиться с пакетом прикладных программ MathCAD, пользуясь системой помощи.

2. Пользуясь операторами и функциями системы MathCAD разработать алгоритм, моделирующий дискретный аналог меандра для 4-6 периодов. Число единичных (и нулевых) отсчетов взять от 5 до 8.

Построить график дискретного аналога меандра.

3. Используя тригонометрические функции разработать алгоритм, моделирующий дискретный аналог гармонического колебания для 3-4 периодов. Шаг дискретизации по фазе взять равным 10, 30, 45, 90 и 120 градусов. Для каждого шага дискретизации построить график.

4. Используя программу генерирования случайных чисел смоделировать отсчеты случайного процесса с равномерным распределением в амплитудном диапазоне -1≤n(k)≥1.Число отсчетов взять равным от 50 до 100.

5
. Смоделировать отсчеты аддитивной смеси двух гармонических сигналов и шума для отношения с/ш = от 1 до 5 по напряжению для 128 отсчетов. Гармонические дискретные сигналы заданы выражениями

где k - номер отсчета

Построить графики сигнала, шума, смеси сигнала с шумом.

6. Распечатать графики дискретных аналогов меандра, дискретной гармонической последовательности для различных фазовых углов дискретизации, дискретной последовательности отсчетов сигнала, шума и смеси сигнал + шум.

7. Индивидуальное задание по построению дискретных аналогов сигналов выдается персонально для каждого студента преподавателем после выполнения общей части лабораторной работы.
4. Содержание отчета.
Отчет должен содержать распечатки программ моделирования испытательных сигналов и графики моделей дискретных сигналов, рассмотренных в пп.3.2 - 3.5.
5. Контрольные вопросы.

1.Какой сигнал называется меандром?


2.Какой сигнал называется детерминированным?


3.Какой сигнал называется случайным?


4.Какой сигнал называется дискретной гармонической последовательностью?


5.Почему удобнее задавать шаг дискретизации через фазовый угол?


6.О чем говорит теорема Котельникова?

7.В какую сторону нужно изменить фазовый угол дискретизации, чтобы увеличить или уменьшить частоту сигнала при неизменном временном шаге дискретизации?
ЛИТЕРАТУРА

1.Гоноровский И.С. Радиотехнические цепи и сигналы.

2.Конспект лекций по курсу "Теоретические основы информационной техники".

ЛАБОРАТОРНАЯ РАБОТА № 2
Вычисление спектра сигналов на ЭВМ с помощью БПФ

1. 
   Цель работы:
   

Научиться находить спектр сигнала с помощью БПФ и по известному спектру находить исходный сигнал с помощью обратного БПФ

2. 
   Краткие теоретические сведения
   

В линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. Говорят, что совокупность векторов {е₁ е₂, е₃, ...}, принадлежащих множеству М, является линейно независимой, если равенство возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов α_i.

Система линейно независимых векторов образует координатный базис в линейном пространстве. Если дано разложение некоторого сигнала s(t) в виде то числа {с₁ с₂, с₃, ...} являются проекциями сигнала s(t) относительно выбранного базиса.

Длину вектора в математике называют его нормой. Линейное пространство сигналов L является нормированным, если каждому вектору однозначно сопоставлено число — норма этого вектора.

В радиотехнике чаще всего полагают, что вещественные аналоговые сигналы имеют норму

(2.1)

Данная формула в равной мере относится как к аналоговым, так и к дискретным сигналам (из двух возможных значений корня выбирается положительное).

Функция u(t), для которой выполняется условие

(2.2)

называется нормированной функцией, а система нормированных функций u₁(t), u₂(t)…, в которой две различные функции взаимно ортогональны, называется ортонормированной системой.

Квадрат нормы носит название энергии сигнала

(2.3)

Определять норму сигнала с помощью формулы (2.1) целесообразно по следующим причинам:

1. В радиотехнике о величине сигнала часто судят, исходя из суммарного энергетического эффекта, например количества теплоты, выделяемой в резисторе.

2. Энергетическая норма оказывается «нечувствительной» к изменениям формы сигнала, может быть, и значительным, но происходящим на коротких отрезках времени.

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции.

Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:

, где n = 1,2,3… (2.4)

Здесь Т — период сигнала.

Два сигнала u и v называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:

(2.5)

Выражение (2.4) называют принципом ортогональности двух сигналов.

Пусть Н — гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени [t₁, t₂], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций {u₀, u₁, u₂, ….u_n, …}, ортогональных друг другу и обладающих единичными нормами:

(2.6)

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

Разложим произвольный сигнал в ряд, согласно следующему выражению

(2.7)

Представление (2.7) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты C_n определяются по формуле:

(2.8)

Совокупность полученных коэффициентов C_n называют спектром сигнала s(t ) в ортогональной системе u(t) и полностью определяют этот сигнал.
Введем основную частоту последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения по формуле (2.8), запишем ряд Фурье для периодического сигнала

(2.9)

с коэффициентами :



(2.10)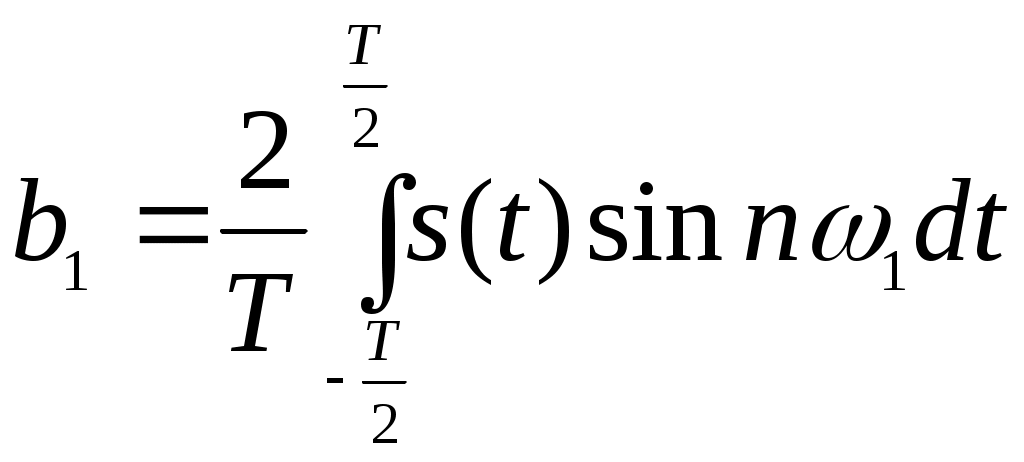


Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами , где (n = 1, 2, 3, ,..), кратными основной частоте последовательности.

Каждую гармонику можно описать ее амплитудой А_n начальной фазой φ_n . Для этого коэффициенты ряда Фурье следует записать в виде:

,

Так что (2.11)

,

Подставив эти выражения в (2.9), получим другую, эквивалентную форму ряда Фурье:



Спектральной диаграммой периодического сигнала принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы.

Для того, чтобы получить комплексную форму ряда Фурье, необходимо выполнить спектральное разложение периодического сигнала, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:

, где (2.12)
В этом случае форма записи ряда Фурье будет выглядеть следующим образом:

(2.13)

А коэффициенты определяются по формуле: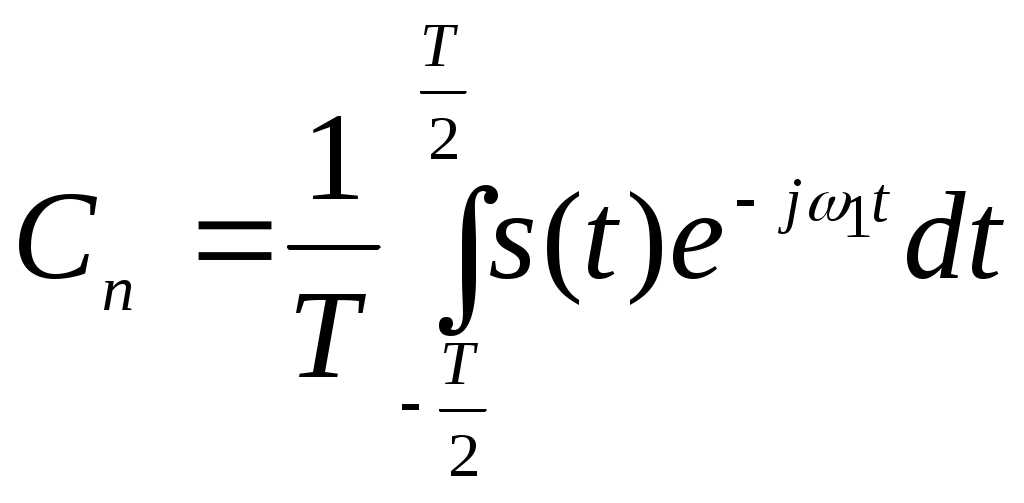

(2.14)

Совокупность коэффициентов C_n ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала.
При разложении периодического сигнала s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут

(2.15)

или

(2.16)

Интервал ортогональности в обоих случаях совпадает с периодом функции s (t).

Система функций (2.15) приводит к тригонометрической форме ряда Фурье, а система (2.16) — к комплексной форме. Между этими двумя формами существует простая связь.

Выражение (2.13) – является разложением в ряд Фурье по системе функций (2.16). Данное выражение легко преобразуется к виду: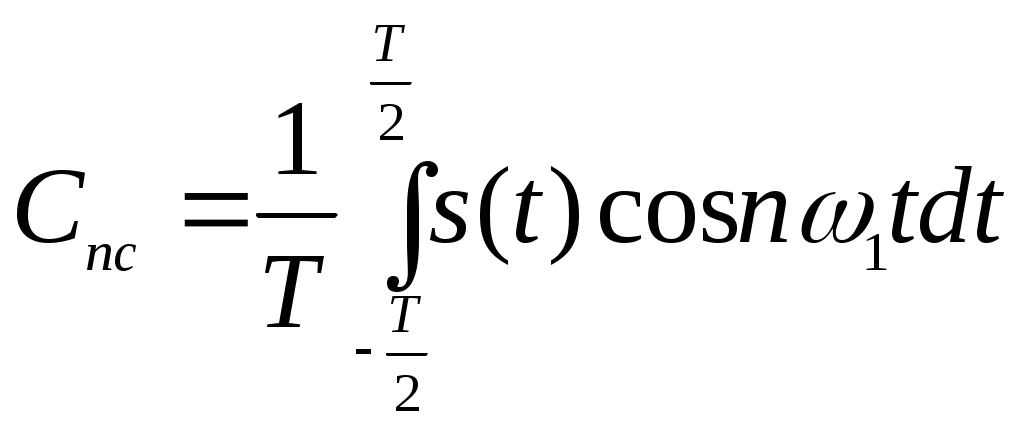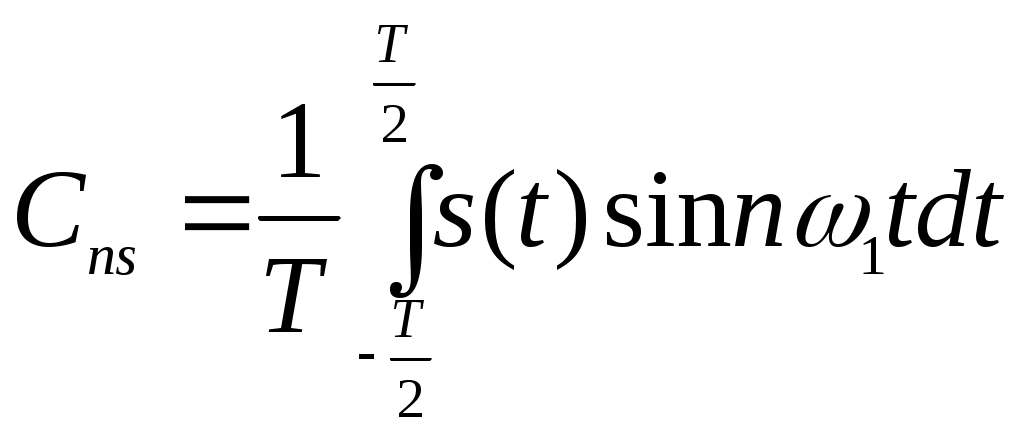

(2.17),

Причем , , гдеC_nc иC_ns - косинусная (действительная) и синусная (мнимая) части коэффициента C_n, определяемы следующим образом:

, (2.18)

Модуль является функцией, четной относительно n, а аргумент θ_n— нечетной, т.е. C_nc является четной, а C_ns – нечетной функциями n.

Теперь нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда (2.17) пару слагаемых, соответствующую какому-либо заданному значению | n | например | n | = 2, и, учтя соотношения и , получим для суммы этих слагаемых выражение, равное .

Отсюда видно, что при переходе к тригонометрической форме ряд (2.17) необходимо записать следующим образом:

(2.19)
Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно- сопряженные пары:

и (2.200

Каждой такой паре отвечает гармоническое колебание



с комплексной амплитудой .Рассмотрим малый интервал частот ∆ω, образующий окрестность некоторого выбранного значения частоты ω₀.В пределах этого интервала будет содержаться отдельных пар спектральных составляющих, частоты которых отличаются сколь угодно мало. Поэтому составляющие можно складывать так, как будто все они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами:

(2.21)

В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала ∆ω:

(2.22)

Функция

(2.23)

носит название спектральной плотности сигнала s(t). Формула (2.23) осуществляет преобразование Фурье данного сигнала.

Физический смысл понятия спектральной плотности.

Интерпретацию полученных результатов удобно провести, перейдя от угловой частоты ω к циклической частоте .

При этом формула (2.22) приобретет вид

(2.24)

Ее надо трактовать так: спектральная плотность есть коэффициент пропорциональности между длиной малого интервала частот ∆f и отвечающей ему комплексной амплитудой ∆A_f0 гармонического сигнала с частотой f₀Коэффициент 2 означает, что вклад в амплитуду дают в равной мере и положительные и отрицательные частоты, образующие окрестности точек ± f₀.

Возможна и обратная процедура – определение сигнала s(t) по его спектральной плотности S(ω):

(2.25)

Формула (2.25) называется обратным преобразованием Фурье для сигнала s(t).
Свойства преобразования Фурье.

1. 
   Линейность.
   

Это важнейшее свойство формулируется так: если имеется некоторая совокупность сигналов s₁(t), s₂(t)…, причем , …,то взвешенная сумма сигналов преобразуется по Фурье следующим образом:

(2.26)

Здесь a_i — произвольные числовые коэффициенты.

2. 
   Свойства вещественной и мнимой частей спектральной плотности.
   

Пусть s(t) — сигнал, принимающий вещественные значения. Его спектральная плотность в общем случае является комплексной:

.

Причем, вещественная часть А(ω) спектральной плотности сигнала есть четная, а мнимая часть В(ω) — нечетная функция частоты:

, . (2.27)

3. Спектральная плотность сигнала, смещенного во времени.

Пусть известно, что для сигнала s(t) существует соответствие . Рассмотрим такой же сигнал, но возникающий на t₀ секунд позднее. Примем точку t₀ за новое начало отсчета времени, обозначим этот смещенный сигнал как s(t - t₀). Тогда:

(2.28)

4. Зависимость спектральной плотности сигнала от выбора масштаба измерения времени.

Предположим, что исходный сигнал s(t) подвергнут изменению масштаба времени. Это означает, что роль времени t играет новая независимая переменная kt (где k — некоторое вещественное число). Еслиk > 1, то происходит «сжатие» исходного сигнала; если же 0 <k <1, то сигнал «растягивается» во времени. Причем, если , то

(2.29)

5. Спектральная плотность производной и неопределенного интеграла.

Пусть сигнал s(t) и его спектральная плотность S(ω) заданы. Рассмотрим новый сигнал и найдем его спектральную плотность F(ω):

(2.30)
При дифференцировании скорость изменения сигнала во времени возрастает. Как следствие, модуль спектра производной имеет большие значения в области высоких частот по сравнению с модулем спектра исходного сигнала.

Формула (2.30) обобщается на случай спектра производной n-го порядка. Очевидно, что если , то

(2.31)

Итак, дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель jω. Поэтому принято говорить, что мнимое числоjω является оператором дифференцирования, действующим в частотной области. Рассмотренная функция является первообразной (неопределенным интегралом) по отношению к функции f(t). Из (2.30) формально следует, что спектр первообразной функции

(2.32)

Таким образом, множитель 1/jω служит оператором интегрирования в частотной области.

6. Спектральная плотность сигнала на выходе интегратора.

Во многих радиотехнических устройствах находят применение так называемые интеграторы — физические системы, выходной сигнал которых пропорционален интегралу от входного воздействия. Рассмотрим интегратор, осуществляющий преобразование входного сигнала s_вх(t) в выходной сигнал s_вых(t) по следующему закону:

(2.33)
Здесь T> 0 - фиксированный параметр. Определенный интеграл, входящий в (2.33), равен разности двух значений первообразной сигнала s_вх(t), одно из которых вычисляется при аргументе t, а другое — при аргументе (t -Т). Используя соотношения (2.26) и (2.28), получаем формулу связи между спектральными плотностями сигналов на входе и выходе:

(2.34)

Сомножитель в скобках ограничен при любых частотах, в то же время модуль знаменателя линейно растет с увеличением частоты. Это свидетельствует о том, что рассматриваемый интегратор действует подобно фильтру нижних частот, ослабляя высокочастотные спектральные составляющие входного сигнала.

7. Спектральная плотность произведения сигналов.

Как известно, при суммировании сигналов их спектры складываются. Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей. Пусть u(t) и v(t) — два сигнала, для которых известны соответствия и . Образуем произведение этих сигналов: и вычислим его спектральную плотность. По общему правилу:

(2.35)

Применив обратное преобразование Фурье, выразим сигнал v(t) через его спектральную плотность и подставим результат в (2.35). Откуда получим следующее выражение:

(2.36)

Интеграл, стоящий в правой части, называют сверткой функций U и V Операция свертки символически обозначается следующим образом:

(2.37)

Таким образом, спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свертке спектральных плотностей сомножителей:

(2.38)
Приведенная выше теорема о свертке может быть обращена: если спектральная плотность некоторого сигнала представляется в виде произведения , причем и , то сигнал является сверткой сигналов s₁(t) и s₂(t), но уже не в частотной, а во временной области:

(2.39)

Для количественного определения степени отличия сигнала и s(t) и его смещенной во времени копии s(t - τ) принято вводить функцию корреляции или автокорреляционную функцию (АКФ) сигнала s(t), равную скалярному произведению сигнала и копии:

(2.40)

Из выражения (2.40) видно, что B_s(t) характеризует степень связи (корреляции) сигнала s(t) со своей копией, сдвинутой на величину τ по оси времени. Ясно, что функция B_s(t) достигает максимума при τ = 0, так как любой сигнал полностью коррелирован с самим собой. При этом

(2.41)

т. е. максимальное значение корреляционной функции равно энергии сигнала.

Квадрат модуля спектральной плотности, как известно, представляет собой энергетический спектр сигнала. Итак, энергетический спектр и автокорреляционная функция связаны преобразованием Фурье:

(2.42)

Ясно, что имеется и обратное соотношение:

(2.43)

Эти результаты принципиально важны по двум причинам. Во-первых, оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.

Часто удобнее вначале получить автокорреляционную функцию, а затем, используя преобразование Фурье, найти энергетический спектр сигнала. Такой прием получил распространение при исследовании свойств сигналов с помощью быстродействующих ЭВМ в реальном масштабе времени.

Сопоставив такому сигналу некоторую математическую модель, можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты. Совокупность этих коэффициентов образует спектр дискретного периодического сигнала.

Воспользуемся моделью в виде последовательности дельта-импульсов и сопоставим исходному колебанию s(t) его дискретное МИП-представление:

(2.44)

Представим дискретную модель (2.44) комплексным рядом Фурье:

(2.45)

с коэффициентами (2.46)

Подставив формулу (2.44) в (2.46), а также используя фильтрующее свойство дельта-функции, получим:

(2.47)

Формула (2.47) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала. Отметим некоторые очевидные свойства ДПФ.

1. Дискретное преобразование Фурье есть линейное преобразование, т. е. сумме сигналов отвечает сумма их ДПФ.

2. Число различных коэффициентов С₀, С₁, С₂, ..., С_N-1 , вычисляемых по формуле (2.47), равно числу N отсчетов за период; при п = N коэффициент C_N = С₀.

3. Коэффициент С₀ (постоянная составляющая) является средним значением всех отсчетов:

(2.48)

4. Если N — четное число, то

(2.49)

5. Пусть отсчетные значения s_k — вещественные числа. Тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряженные пары:

(2.50)

Поэтому можно считать, что коэффициенты C_N/2+1, ..., C_N-1 отвечают отрицательным частотам. При изучении амплитудного спектра сигнала они не дают новых сведений.

Задача диск-ретного спектрального анализа может быть поставлена и по-иному. Допустим, что коэффициенты С_n , образующие ДПФ, заданы. Положим в формуле (2.47) t = k∆t и учтем, что суммируется лишь конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала. Таким образом, получаем формулу для вычисления отсчетных значений:

, (2.51)

выражающую алгоритм обратного дискретного преобразования Фурье (ОДПФ).

Взаимно дополняющие друг друга формулы (2.47) и (2.51) являются дискретными аналогами обычной пары преобразований Фурье для непрерывных сигналов.

В настоящее время дискретный спектральный анализ является одним из наиболее распространенных методов исследования сигналов с помощью компьютеров. Алгоритмы вычисления ДПФ и БПФ реализованы в таких широко распространенных прикладных математических пакетах, как Maple и MathCAD.

Как видно из

формулы (2.47) или (2.51) чтобы вычислить ДПФ или ОДПФ последовательности из N элементов, требуется выполнить N² операций с комплексными числами. Если длины обрабатываемых массивов имеют порядок тысячи или более, то использовать эти алгоритмы дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств.

Выходом из положения явился алгоритм быстрого преобразования Фурье (БПФ), предложенный в 60-х годах. Существенно сократить число выполняемых операций здесь удается за счет того, что обработка входного массива сводится к нахождению ДПФ (или ОДПФ) массивов с меньшим числом членов.

Будем предполагать, и это существенно для метода БПФ, что число отсчетов N=2^Р, где р - целое число.

Разобьем входную последовательность {s_k} на две части с четными и нечетными номерами:

(2.52)

и представим n-й коэффициент ДПФ в виде



Непосредственно видно, что первая половина коэффициентов ДПФ исходного сигнала с номерами от 0 до N/2—1 выражается через коэффициенты ДПФ двух частных последовательностей: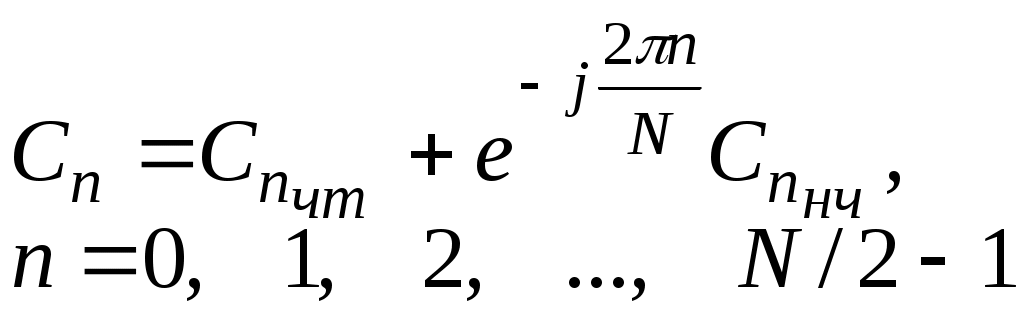

(2.53)

Теперь учтем, что последовательности коэффициентов, относящихся к четной и нечетной частям входного массива, являются периодическими с периодом N/2:



Кроме того, входящий в формулу (2.53) множитель при n≥N/2 можно преобразовать так:



Отсюда находим выражение для второй половины множества коэффициентов ДПФ: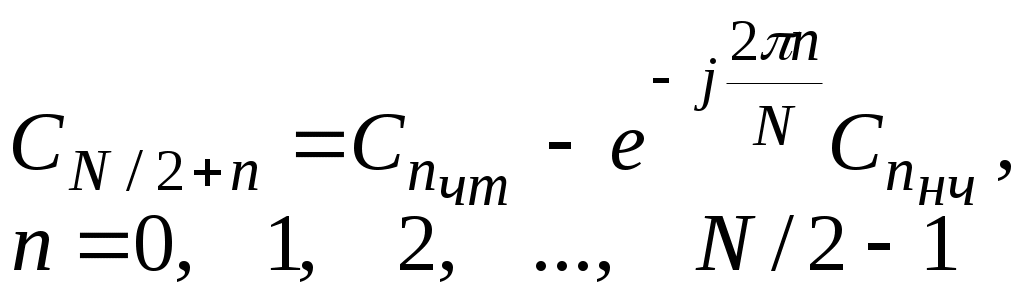

(2.54)

Формулы (2.53) и (2.54) лежат в основе алгоритма БПФ. Далее вычисления строят по итерационному принципу: последовательности отсчетов с четными и нечетными номерами вновь разбивают на две части. Процесс продолжают до тех пор, пока не получится последовательность, состоящая из единственного элемента. Легко видеть, что ДПФ этого элемента совпадает с ним самим.

Можно показать, что число операций, необходимых для вычисления БПФ, оценивается как .

БПФ обладает всеми свойствами дискретного преобразования Фурье:

-БПФ есть линейное преобразование, то есть сумме сигналов отвечает сумма их БПФ

-Число различных коэффициентов C₀,С₁,C₃,...C_N, вычисляемых с помощью БПФ равно числу N отсчетов за период. Причем С_n=C₀.

-Коэффициент С₀есть постоянная составляющая.

-Если отсчетные значения сигнала  вещественные числа, то коэффициенты, симметричные относительно номера N/2 образуют сопряженные пары. Поэтому коэффициенты с номерами N/2+1,...,N-1 отвечают отрицательным частотам. При изучении спектра они не дают новых сведений о сигнале и не вычисляются. Если коэффициенты С_n, образующие БПФ, заданы, то по ним, используя алгоритм обратного БПФ, можно получить отсчетные значения сигнала на периоде.

По известным коэффициентам БПФ C₀,C₁,...,C_N/2 можно восстановить исходный непрерывный сигнал s(t) c ограниченным спектром, который был подвергнут дискретизации:

,

где _i= аrg C_i  фазовый угол коэффициента БПФ.
3. Порядок выполнения работы
1. В MathCAD-е задать алгоритм, моделирующий отсчеты одиночного импульса. Общее число отсчетов взять равным 128, из которых первых 8 равны 1, остальные 0.

2. Используя функцию вычисления БПФ определить коэффициенты БПФ.

3. Так как коэффициенты являются комплексными, то по ним определите АЧХ и ФЧХ дискретного спектра прямоугольного импульса.

4. Вывести на экран и на печать графики АЧХ и ФЧХ для различных длительностей импульса, меняя число единичных отсчетов.

5. Задать отсчеты сигнала (128 отсчётов)

,

вывести на экран его график

6. С помощью БПФ найти спектр этого сигнала.

7. Добавить шум к дискретному сигналу s(i).

8. Вывести на экран график смеси сигнала с шумом.

9. С помощью БПФ найти спектр шума и смеси сигнала с шумом.

10. С помощью обратного БПФ найти исходный сигнал.

11. Используя статистические функции МАТКАДА определить среднее значение, дисперсию ср.кв.отклонение шума.

12. Задать отсчеты сигнала типа синусоиды со случайной фазой. Для задания выборок фазы использовать генератор случайных чисел МАТКАДА с распределением в диапазоне от 0 до 2.

13. Найти спектр сигнала п.12.

14. Задать отсчеты сигнала типа синусоиды со случайной амплитудой.

,

где А(i) -отсчеты шума с распределением в диапазоне от 0 до 0,2.

15. Найти спектр сигнала п.14.

16. Используя из набора статистических функций МАТКАДА функцию сглаживания (medsmooth(x,v)), выполнить сглаживание сигнала п.14 и п.7. Задать отсчеты сигнала типа синусоиды со случайной амплитудой и случайной фазой.
4. Содержание отчета.
Отчет должен содержать распечатки графиков сигналов и их спектров(АЧХ и ФЧХ).
5.Контрольные вопросы.
1.Назовите основные свойства преобразования Фурье.