Лабораторная работа №1.
Оценка количества информации. Работа с позиционными системами счисления.
Количество информации
Системы счисления
ЗАДАНИЯ
Контрольные вопросы
Количество информации
1.1 Количество информации как мера уменьшения неопределенности знаний
Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию. Сообщения обычно содержат информацию о каких-либо событиях. Количество информации для событий с различными вероятностями определяется по формуле Шеннона:
(1) 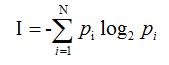
где I – количество информации,
N – количество возможных событий,
pi – вероятности отдельных событий.
Если события равновероятны, то количество информации определяется по формуле Хартли:
(2) I = log2 N
или из показательного уравнения:
(3) N = 2I
Пример 1. При подбрасывании монеты возможны 2 исхода: «орел» и «решка». Какое количество информации будет содержать сообщение о выпадении одного из двух возможных результатов.
События равновероятны, поэтому для определения количества информации, содержащимся в сообщении о выпадении «орла» или «решки», воспользуемся формулой 2:
N=2
I=log2 2 = 1 бит
Пример 2. В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 зеленых и 40 синих шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика.
Так как количество шариков различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета деленному на общее количество шариков:
pб = 0,1; pк = 0,2; pз = 0,3; pс= 0,4.
События неравновероятны, поэтому для определения количества информации, содержащимся в сообщении о цвете шарика, воспользуемся формулой 1:
I = - (0,1×log2 0,1+0,2×log2 0,2+0,3×log2 0,3+0,4×log2 0,4) бит
1.2 Единицы измерения количества информации
За единицу количества информации принят 1 бит — количество информации, содержащееся в сообщении, уменьшающем неопределенность знаний в два раза.
Принята следующая система единиц измерения количества информации:
1 байт = 8 бит
1 Килобайт = 210 байт = 1024 байт
1 Мегабайт = 220 байт = 1024 Килобайт
1 Гигабайт = 230 байт = 1024 Мегабайт
1 Терабайт = 240 байт = 1024 Гигабайт
1 Петабайт = 250 байт = 1024 Терабайт
1 Экзабайт = 260 байт = 1024 Петабайт
1 Зеттабайт = 270 байт = 1024 Экзабайт
1 Йоттабайт = 280 байт = 1024 Зеттабайт
1.3 Определение количества информации, представленной с помощью знаковых систем
Если рассматривать символы алфавита как множество возможных сообщений (событий) N, то количество информации, которое несет один знак можно определить из формулы 1. Если считать появление каждого знака алфавита в тексте событиями равновероятными, то для определения количества информации можно воспользоваться формулой 2 или уравнением 3.
Количество информации, которое несет один знак алфавита тем больше, чем больше знаков входят в этот алфавит, т.е. чем больше мощность алфавита.
Количество информации, содержащейся в сообщении, закодированном с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении.
Пример 3.Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Килобайта.
Арифметически перевести информационный объем сообщения в биты:
I = 1,25×1024×8 = 10 240 бит
Определить количество бит, приходящееся на один символ:
10 240 бит : 2 048 = 5 бит
По формуле 3 определить количество символов в алфавите:
N = 25=32 символа в алфавите.
2. Системы счисления
2.1 Правило перевода чисел из системы произвольным основанием в десятичную систему счисления
Для перевода целого числа в десятичную систему счисления достаточно представить целую часть числа в виде суммы произведений цифры числа на основание в степени начиная с нулевой справа налево. Для перевода дробной части числа ее так же необходимо представить в виде суммы произведений цифры числа на основание в степени начиная с -1 слева направо. Вычислить полученное выражение. Например:
10102=1 ·23+ 0 ·22 + 1 ·21 + 0 ·20 = 1010
1B16=1 ·161+ 11 ·160 = 2710
11,01 2 = 1 ·21 + 1 ·20 + 0 ·2-1 + 1 ·2-2 = 3,2510
7,28=7 ·80+ 2 ·8-1 = 7,2510
2.2 Правило перевода чисел из десятичной системы счисления в систему счисления с произвольным основанием
Целое число делится нацело на основание системы счисления, затем на это основание делятся все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. В результат заносится последнее частное и все остатки от деления, начиная с последнего.
Пример. Переведем число 23 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
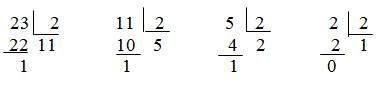
Следовательно 2310=101112

2310=278 2310=1716
Для перевода правильной дроби из одной системы счисления в другую необходимо выполнить следующие действия:
• отделить вертикальной чертой дробную часть от целой;
• умножить дробную часть на основание новой системы счисления, записав результат строго под исходным числом, начиная с младшего разряда; в случае, если получится перенос в целую часть числа, записать его слева от вертикальной черты;
• дробную часть полученного числа снова умножить на основание новой системы счисления и т.д.; умножение выполнять до тех пор, пока либо будет полученное число с заданной точностью, либо справа от вертикальной черты окажется нуль.
Результатом перевода будет число, полученное слева от вертикальной черты, при чтении сверху вниз. При выполнении перевода необходимо умножение производить в исходной системе счисления и основание новой системы счисления тоже представить в исходной системе.
Пример: Перевести число 0,728 в восьмеричную систему:
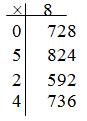 Следовательно0,72810=0,5248 Следовательно0,72810=0,5248
Для перевода неправильной дроби следует отдельно перевести целую часть, отдельно дробную часть.
2.3 Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления и обратный перевод.
При переводе двоичного числа в восьмеричную систему счисления в двоичном числе справа налево выделяю группы по три разряда в каждой (триады) и каждую такую тройку записывают в виде восьмеричной цифры. Если в группе, куда входят старшие разряды числа, нет трех разрядов, то недостающие подразумеваются равными нулю.
При переводе двоичного числа в шестнадцатеричную систему счисления в двоичном числе справа налево выделяю группы по четыре разряда в каждой (тетрады) и каждую такую четверку записывают в виде шестнадцатеричной цифры. Если в группе, куда входят старшие разряды числа, нет четырех разрядов, то недостающие подразумеваются равными нулю.
Перевод из восьмеричной (шестнадцатеричной) системы счисления выполняются аналогично: один символ восьмеричной заменяется тремя двоичными, один символ шестнадцатеричной заменяется четырьмя двоичными.
Примеры:
1) Переведем число в восьмеричную систему счисления.
Для этого разобьем данное число справа налево на тройки (триады). Каждую триаду заменим соответствующим восьмеричным числом.
101112→010 111 2→278
2) Переведем число в шестнадцатеричную систему счисления.
Для этого разобьем данное число справа и слева от запятой на четверки (тетрады) справа налево. Каждую тетраду заменим соответствующим шестнадцатеричным числом.
101112→0001 0111 2→1716
3) Переведем число из шестнадцатеричной системы счисления в двоичную.
Для этого представим каждую шестнадцатеричную цифру соответствующим двоичным числом.
2CE16→10 1100 1110 2
ЗАДАНИЯ
№ варианта
|
Задание
|
№ варианта
|
Задание
|
1
|
1) 1111111010 (2)→(10); 427 (8) → (10);
3DC5 (16) →(10);
2) 99176 (10) →(2),(8),(16);
3) 0.97 (10) →(2) до 6 знаков после запятой;
4) 576431 (8)→(16); 3EFA (16)→(8);
5) 426 (8)*456 (8); FA3 (16)+3D (16)
6) Какое количество информации несет в себе сообщение о том, что нужная вам программа находится на одной из восьми flash-карт?
|
2
|
1) 1011001010 (2)→(10); 761 (8) → (10);
2BA8(16) →(10);
2) 7965(10) →(2),(8),(16);
3) 0.67 (10) →(2) до 6 знаков после запятой;
4) 42637 (8)→(16); FA34B (16)→(8);
5) 751 (8)*63 (8);DA3 (16)+F41(16)
6) Какое количество информации получил второй игрок при игре в крестики-нолики на поле 8Х8, после первого хода первого игрока.
|
3
|
1) 1000000110 (2)→(10); 645 (8) → (10);
F451 (16) →(10);
2) 7841 (10) →(2),(8),(16);
3) 0.34 (10) →(2) до 6 знаков после запятой;
4) 547221 (8)→(16); EF410 (16)→(8);
5) 763 (8)*215 (8); 40E (16)+3B (16)
6) В рулетке общее количество лунок равно 128. Какое количество информации получим в зрительном сообщении об остановки шарика в одной из лунок.
|
4
|
1) 101010101 (2)→(10); 571(8) → (10);
4ED(16) →(10);
2) 9917(10) →(2),(8),(16);
3) 0.27 (10) →(2) до 6 знаков после запятой;
4) 63451 (8)→(16); A310E(16)→(8);
5) 741 (8)*32(8);45A (16)+B19(16)
6) Заполните пропуски числами: _ Гбайт=1536 Мбайт = _Кбайт
|
5
|
1) 1111000111 (2)→(10); 2651 (8) → (10);
F43 (16) →(10);
2) 5674 (10) →(2),(8),(16);
3) 0.56 (10) →(2) до 6 знаков после запятой;
4) 567412 (8)→(16); DE432A (16)→(8);
5) 452 (8) * 321(8); E41 (16)+40D (16)
6) Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся: 30 белых, 30 зеленых, 30 синих и 10 красных шариков.
|
6
|
1) 11100011100 (2)→(10); 327(8) → (10);
43A(16) →(10);
2) 2288(10) →(2),(8),(16);
3) 0.62 (10) →(2) до 6 знаков после запятой;
4) 615044 (8)→(16); FF410A(16)→(8);
5) 645 (8)*123(8);F51(16)+A09(16)
6) Найти х из следующего соотношения:16х бит=32 Мбайт.
|
7
|
1) 1000011101 (2)→(10); 7452(8) → (10);
42E (16) →(10);
2) 884411 (10) →(2),(8),(16);
3) 0.55 (10) →(2) до 6 знаков после запятой;
4) 223377 (8)→(16); 33AA11 (16)→(8);
5) 551 (8)*332(8); AA9 (16)+559 (16)
6) Заполните пропуски числами: _ Кбайт = _ байт = 213 бит
|
8
|
1) 1110001110 (2)→(10); 654(8) → (10);
5EA(16) →(10);
2) 65871(10) →(2),(8),(16);
3) 0.77 (10) →(2) до 6 знаков после запятой;
4) 65417 (8)→(16); 65EA1(16)→(8);
5) 741 (8)*65(8);4EA(16)+5A1(16)
6) Какова мощность алфавита с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/512 часть одного мегабайта.
|
9
|
1) 111011011 (2)→(10); 5741(8) → (10);
76A (16) →(10);
2) 9475 (10) →(2),(8),(16);
3) 0.123 (10) →(2) до 6 знаков после запятой;
4) 557741 (8)→(16); F432A (16)→(8);
5) 664 (8) * 103(8); AE4 (16) + 6F7 (16)
6) Пользователь компьютера может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере равна 256. Какое количество информации в байтах может ввести пользователь в компьютер за 1 минуту.
|
10
|
1) 11100011010 (2)→(10); 651(8) → (10);
F4A(16) →(10);
2) 6971(10) →(2),(8),(16);
3) 0.94 (10) →(2) до 6 знаков после запятой;
4) 223547 (8)→(16); 147E3(16)→(8);
5) 341 (8) * 76(8);F41(16) + ED4(16)
6) Заполните пропуски числами: 512 Кбайт = 2_ байт = 2_ бит
|
11
|
1) 111011101 (2)→(10); 55661(8) → (10);
5554 (16) →(10);
2) 77416 (10) →(2),(8),(16);
3) 0.32 (10) →(2) до 6 знаков после запятой;
4) 664410 (8)→(16); 4509A (16)→(8);
5) 456 (8) * 231(8); DE4 (16) + 56A (16)
6) Система оптического распознавания символов позволяет преобразовать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65536 символов. Какое количество информации будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов.
|
12
|
1) 111011100 (2)→(10); 5571(8) → (10);
E41(16) →(10);
2) 36971(10) →(2),(8),(16);
3) 0.125 (10) →(2) до 6 знаков после запятой;
4) 6644417 (8) →(16); 14DE40(16) →(8);
5) 745 (8) * 76(8);A32(16) + 45F(16)
6) Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке хранятся: 25 белых, 25 зеленых, 25 синих и 25 красных шариков.
|
13
|
1) 111000010 (2)→(10); 66547(8) → (10);
90A1 (16) →(10);
2) 44457 (10) →(2),(8),(16);
3) 0.77 (10) →(2) до 6 знаков после запятой;
4) 336471 (8)→(16); E4320 (16)→(8);
5) 235 (8) * 76(8); 45A (16) + E41 (16)
6) Заполните пропуски числами: 5 Кбайт =_ байт = _ бит
|
14
|
1) 110110110 (2)→(10); 55741(8) → (10);
E4A(16) →(10);
2) 9947(10) →(2),(8),(16);
3) 0.64 (10) →(2) до 6 знаков после запятой;
4) 745321 (8) →(16); AE421(16) →(8);
5) 457 (8) * 75(8);E8A(16) + 123(16)
6) Найти х из следующего соотношения:8х Кбайт=16 Гбайт.
|
15
|
1) 111000011 (2)→(10); 666441(8) → (10);
5554 (16) →(10);
2) 46781 (10) →(2),(8),(16);
3) 0.124 (10) →(2) до 6 знаков после запятой;
4) 6655107 (8)→(16); 5561A32 (16)→(8);
5) 645 (8) * 321(8); E41 (16) + 569 (16)
6) Происходит выбор одной карты из колоды в 32 карты. Какое количество информации получим в зрительном сообщении о выборе определенной карты.
|
16
|
1) 111000110 (2)→(10); 32174(8) → (10);
231A(16) →(10);
2) 3355781(10) →(2),(8),(16);
3) 0.61 (10) →(2) до 6 знаков после запятой;
4) 75641 (8) →(16); DE41A(16) →(8);
5) 321 (8) * 127(8);E8A(16) + EA3(16)
6) Заполните пропуски числами: _ Кбайт=_байт=12288 бит.
|
17
|
1) 11100011 (2)→(10); 607441(8) → (10);
5AE4 (16) →(10);
2) 65874 (10) →(2),(8),(16);
3) 0.42 (10) →(2) до 6 знаков после запятой;
4) 312540 (8)→(16); EA321 (16)→(8);
5) 312 (8) * 67(8); EA3 (16) + 645 (16)
6) Цветное растровое графическое изображение, палитра которого включает в себя 65 536 цветов, имеет размер 100Х100 точек (пикселей). Какой объем видеопамяти компьютера (в Кбайтах) занимает это изображение в формате BMP?
|
18
|
1) 111100010 (2)→(10); 31254(8) → (10);
931A(16) →(10);
2) 32574(10) →(2),(8),(16);
3) 0.85 (10) →(2) до 6 знаков после запятой;
4) 741255 (8) →(16); FE4321(16) →(8);
5) 574 (8) * 64(8);EA2(16) + 90A(16)
6) Сколько символов содержит сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Мбайта?
|
19
|
1) 101001010 (2)→(10); 67547(8) → (10);
90A4 (16) →(10);
2) 45247 (10) →(2),(8),(16);
3) 0.88 (10) →(2) до 6 знаков после запятой;
4) 302141 (8)→(16); ED1A0 (16)→(8);
5) 741 (8) * 76(8); 45A (16) + E41 (16)
6) Сколько килобайтов составит сообщение из 384 символов 16-ти символьного алфавита?
|
20
|
1) 1111100010 (2)→(10); 55741(8) → (10);
EE7(16) →(10);
2) 332417(10) →(2),(8),(16);
3) 0.33 (10) →(2) до 6 знаков после запятой;
4) 524721 (8) →(16); FA231(16) →(8);
5) 564 (8) * 75(8);E8A(16) + 123(16)
6) Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
|
21
|
1) 100111011 (2)→(10); 5741(8) → (10);
76A (16) →(10);
2) 9645 (10) →(2),(8),(16);
3) 0.887 (10) →(2) до 6 знаков после запятой;
4) 500411 (8)→(16); FA3A (16)→(8);
5) 336 (8) * 103(8); AE3 (16) + 6F7 (16)
6) Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
|
22
|
1) 1110101010 (2)→(10); 651(8) → (10);
F32(16) →(10);
2) 68711(10) →(2),(8),(16);
3) 0.125 (10) →(2) до 6 знаков после запятой;
4) 66541 (8)→(16); 45EA1(16)→(8);
5) 541 (8) * 64(8);F41(16) + DA9(16)
6) Племя Мульти имеет 32-х символьный алфавит. Племя Пульти использует 64-х символьный алфавит. Вожди племен обменялись письмами. Письмо племени Мульти содержало 80 символов, а письмо племени Пульти — 70 символов. Сравните объемы информации, содержащейся в письмах.
|
23
|
1) 10111001 (2)→(10); 507441(8) → (10);
34DA (16) →(10);
2) 65874 (10) →(2),(8),(16);
3) 0.66 (10) →(2) до 6 знаков после запятой;
4) 313240 (8)→(16); FA211 (16)→(8);
5) 455 (8) * 67(8); EA2 (16) + 645 (16)
6) Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
|
24
|
1) 111000111 (2)→(10); 32124(8) → (10);
830A(16) →(10);
2) 55414(10) →(2),(8),(16);
3) 0.64 (10) →(2) до 6 знаков после запятой;
4) 654512 (8) →(16); AE231(16) →(8);
5) 645 (8) * 64(8);EA2(16) + 90A(16)
6) Два сообщения содержат одинаковое количество символов. Количество информации в первом тексте в 1,5 раза больше, чем во втором. Сколько символов содержат алфавиты, с помощью которых записаны сообщения, если известно, что число символов в каждом алфавите не превышает 10 и на каждый символ приходится целое число битов?
|
25
|
1) 110000011 (2)→(10); 666441(8) → (10);
589A (16) →(10);
2) 77841 (10) →(2),(8),(16);
3) 0.181 (10) →(2) до 6 знаков после запятой;
4) 774125 (8)→(16); 9A1A32 (16)→(8);
5) 741 (8) * 121(8); AD1 (16) + 569 (16)
6) Жители планеты Принтер используют алфавит из 256 знаков, а жители планеты Плоттер — из 128 знаков. Для жителей какой планеты сообщение из 10 знаков несет больше информации и на сколько?
|
26
|
1) 1010100110 (2)→(10); 32174(8) → (10);
231A(16) →(10);
2) 99557(10) →(2),(8),(16);
3) 0.88 (10) →(2) до 6 знаков после запятой;
4) 332250 (8) →(16); DE90A(16) →(8);
5) 547 (8) * 125(8);E8A(16) + EA3(16)
6) В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что достали клубок красной шерсти?
|
27
|
1) 11100011 (2)→(10); 607441(8) → (10);
5AE4 (16) →(10);
2) 9741 (10) →(2),(8),(16);
3) 0.55 (10) →(2) до 6 знаков после запятой;
4) 445502 (8)→(16); EA321 (16)→(8);
5) 312 (8) * 67(8); DA3 (16) + 645 (16)
6) В кодировке Unicode каждый символ закодирован двухбайтовым словом. Определите информационный объем следующего предложения в этой кодировке: Я сдаю экзамен по информатике.
|
28
|
1) 110011010 (2)→(10); 31254(8) → (10);
931A(16) →(10);
2) 9871(10) →(2),(8),(16);
3) 0.124 (10) →(2) до 6 знаков после запятой;
4) 4654 (8) →(16); FE4321(16) →(8);
5) 574 (8) * 64(8);EA2(16) + 90A(16)
6) Информационный объем текста, набранного в кодировке unicode (1 символ закодирован 2 байтами), равен 1,5 Мбайт. Сколько символов в этом тексте?
|
29
|
1) 10111011 (2)→(10); 16571(8) → (10);
76E1 (16) →(10);
2) 1852 (10) →(2),(8),(16);
3) 0.67 (10) →(2) до 6 знаков после запятой;
4) 7712302 (8)→(16); 76D2 (16)→(8);
5) 452 (8) * 67(8); 8E9 (16) + 5A7 (16)
6) Дан текст из 600 символов. Известно, что символы берутся из таблицы размером 16 на 32. Определите информационный объем текста в битах.
|
30
|
1) 10011010 (2)→(10); 5414(8) → (10);
56A2(16) →(10);
2) 3324(10) →(2),(8),(16);
3) 0.17 (10) →(2) до 6 знаков после запятой;
4) 66541 (8) →(16); FE4984(16) →(8);
5) 571 (8) * 64(8);EA2(16) + 64A(16)
6) Мощность алфавита равна 64. Сколько Кбайт памяти потребуется, чтобы сохранить 128 страниц текста, содержащего в среднем 256 символов на каждой странице?
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
По какой формуле определяется количество информации для событий с различными вероятностями?
По какой формуле определяется количество информации, если события равновероятны?
Как определить количество информации, представленной с помощью знаковых систем?
Перечислите единицы измерения количества информации.
Что такое бит, байт?
Что такое система счисления?
В чем отличие позиционной системы счисления от непозиционной?
Как можно представить запись произвольного числа в P–ичной системе счисления?
Назовите преимущества двоичной системы счисления перед другими системами.
В чем заключается правило перевода чисел из системы произвольным основанием в десятичную систему счисления?
Как перевести числа из десятичной системы счисления в систему счисления с произвольным основанием?
Как осуществляется перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления?
|
 Скачать 108 Kb.
Скачать 108 Kb.
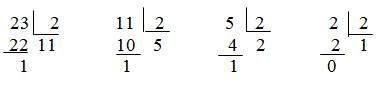

 Следовательно0,72810=0,5248
Следовательно0,72810=0,5248 