А491_ЛР№1_БарановаАА. Лабораторная работа 1 Определение аэродинамических характеристик осесимметричного тела
 Скачать 265.14 Kb. Скачать 265.14 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д.Ф. УСТИНОВА  Дисциплина Механика жидкости и газа Лабораторная работа № 1 Определение аэродинамических характеристик осесимметричного тела
Санкт-Петербург 2021 г. Цель работы – определить аэродинамические коэффициенты cx, cy и cmz осесимметричного оперенного тела вращения в функции от угла атаки α, найти положение центра давления относительно центра тяжести в зависимости от угла атаки α. Силовое воздействие потока на модель тела вращения определить с помощью замера сил на аэродинамических весах. 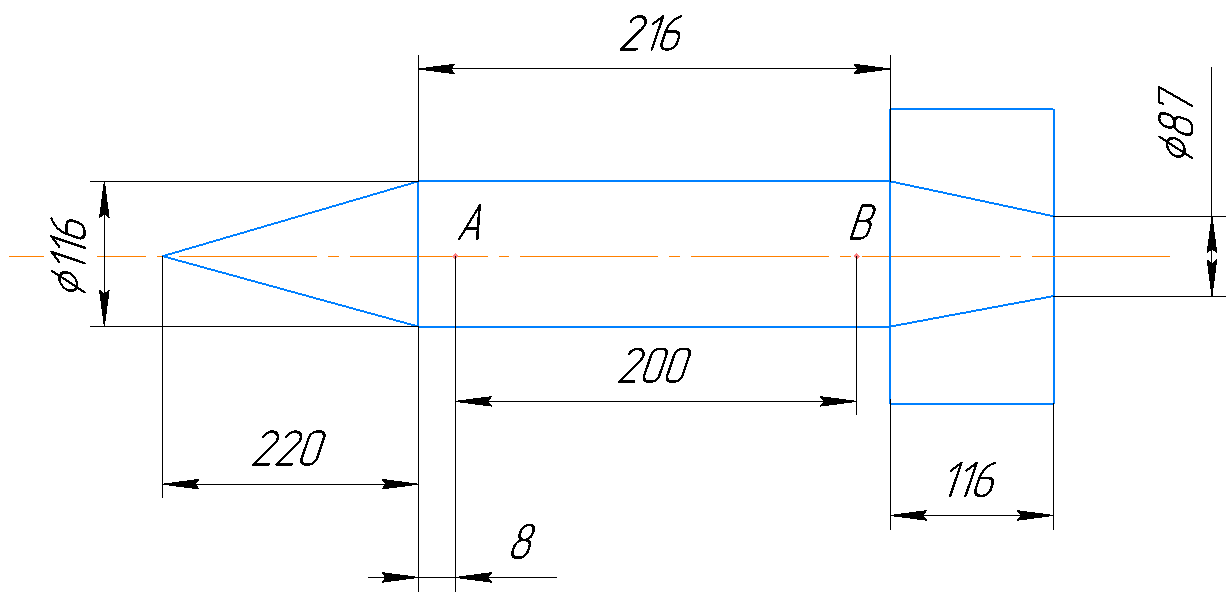 Рис.1. Чертеж модели 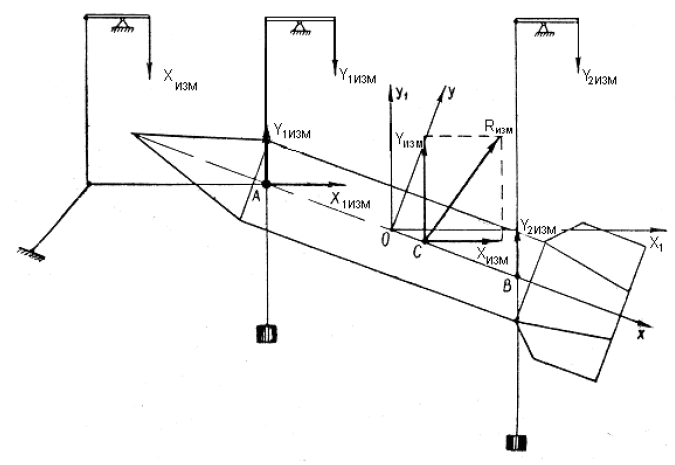 Рис.2. Схема сил и координатных осей В ходе выполнения лабораторной работы были сняты необходимые для расчета данные, указанные в таб.1. Таблица 1
1. Расчет силы лобового сопротивления, составляющие подъемной силы и саму подъемную силу по формулам: 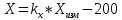 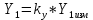 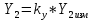 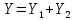 При α=0̊ 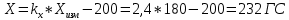 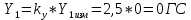 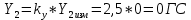 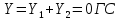 При α=4̊ 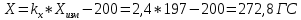 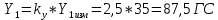 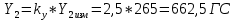 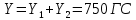 При α=8̊ 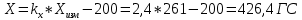 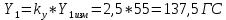 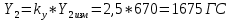 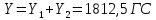 При α=12̊ 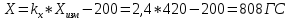 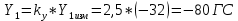 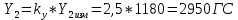 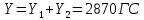 2. Вычисление площади поперечного сечения миделя модели, скоростной напор и скорость натекающего потока 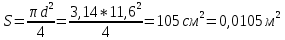 Скоростной напор рассчитывается по формуле: 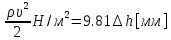 Для расчета скоростного напора стоит использовать среднее значение 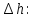 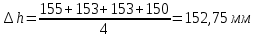 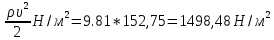 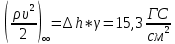 Зная скоростной напор, вычисляем скорость натекающего потока 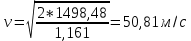 3. После определения значения 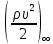 найдем аэродинамические коэффициенты сх, cy и cy2 по формулам: найдем аэродинамические коэффициенты сх, cy и cy2 по формулам: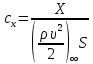 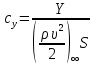 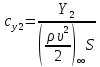 При α=0̊ 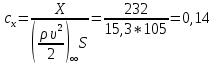 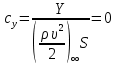 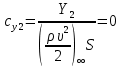 При α=4̊ 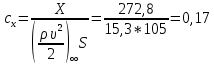 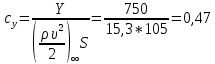 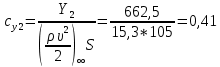 При α=8̊ 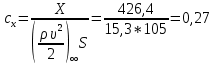 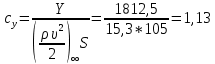 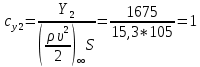 При α=12̊ 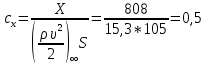 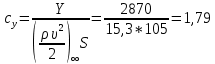 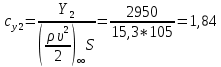 4. Найдем значения коэффициентов cx0, a1, a2, a3, a4, a5 с помощью обработки экспериментальных данных методом наименьших квадратов, будем брать угол α в радианах. 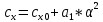 ; ;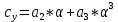 ; ;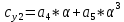 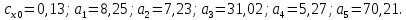 5. Определение положение центра давления С. 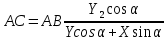 Разделим числитель и знаменатель дроби на 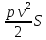 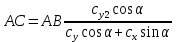 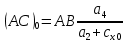 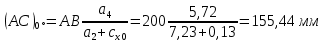 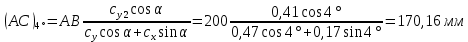 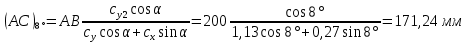 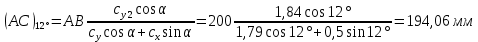 Найденное соотношение дает положение центра давления С на оси тела вращения относительно точки А. Необходимо ориентировать точку С относительно центра тяжести. Поэтому нужно найти центр тяжести всей модели в целом. В частности, для простоты можно считать модель сплошной и однородной, состоящей из трех составных частей: носовой (1), центральной (2) и кормовой (3) (весом оперения пренебрегаем). 6. Определение положения центра тяжести. Для круглого прямого усеченного конуса: 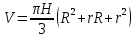 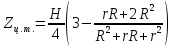 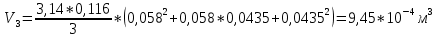 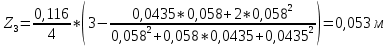 Для полного конуса (r=0): 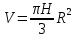 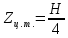 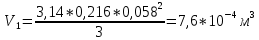 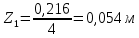 Для цилиндра: 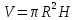 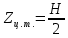 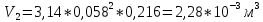 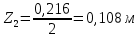 Положение центра тяжести модели х0определяется по формуле: 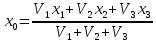 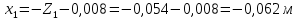 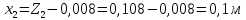 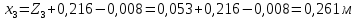 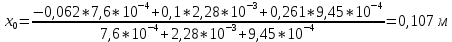 7. Определение расстояния вдоль оси между центром тяжести и центром давления: 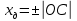 , где , где 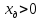 , если точка С находится перед точкой О. , если точка С находится перед точкой О.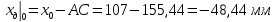 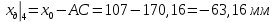 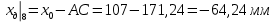 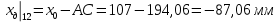 8. Определение значения коэффициента сmz для каждого угла атаки и коэффициенты аппроксимирующего зависимость сmz= сmz(α) полинома. 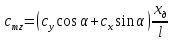 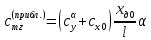 При α=0̊ 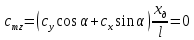 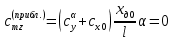 При α=4̊ 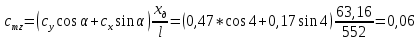 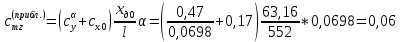 При α=8̊ 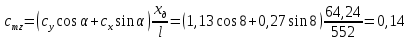 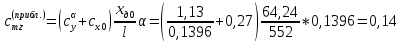 При α=12̊ 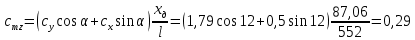 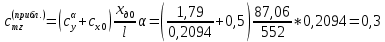 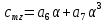 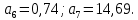 Полученные в расчетах данные заносим в таблицу 1. Таблица 1. «Результаты вычислений»
Согласно нашим данным построим графики зависимостей: 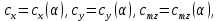 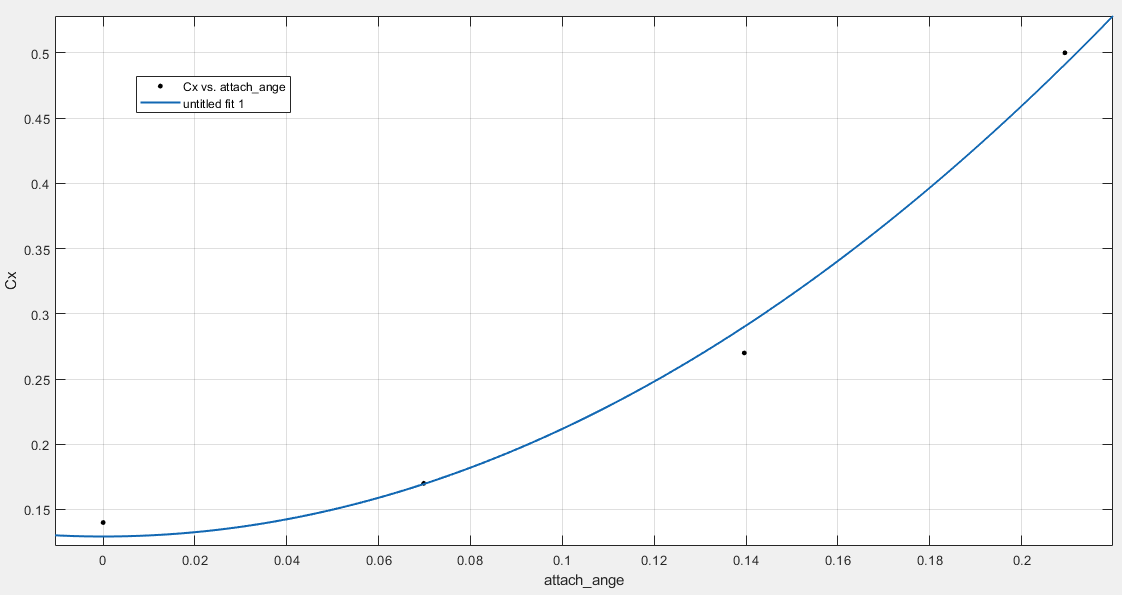 Рис.1. «График зависимости Рис.1. «График зависимости 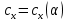 » »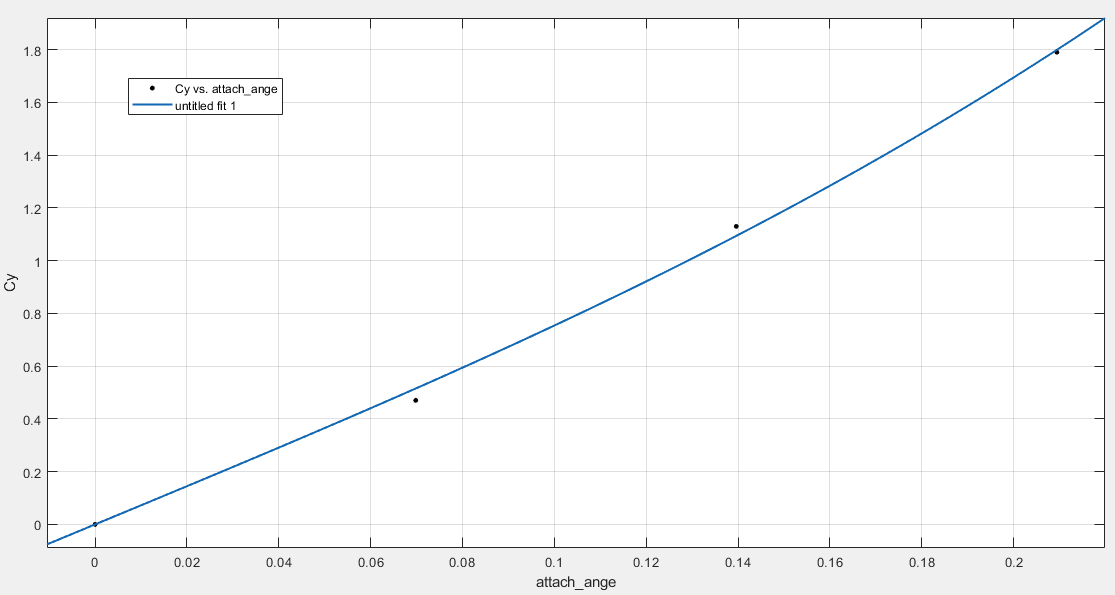 Рис.2. «График зависимости Рис.2. «График зависимости 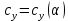 » »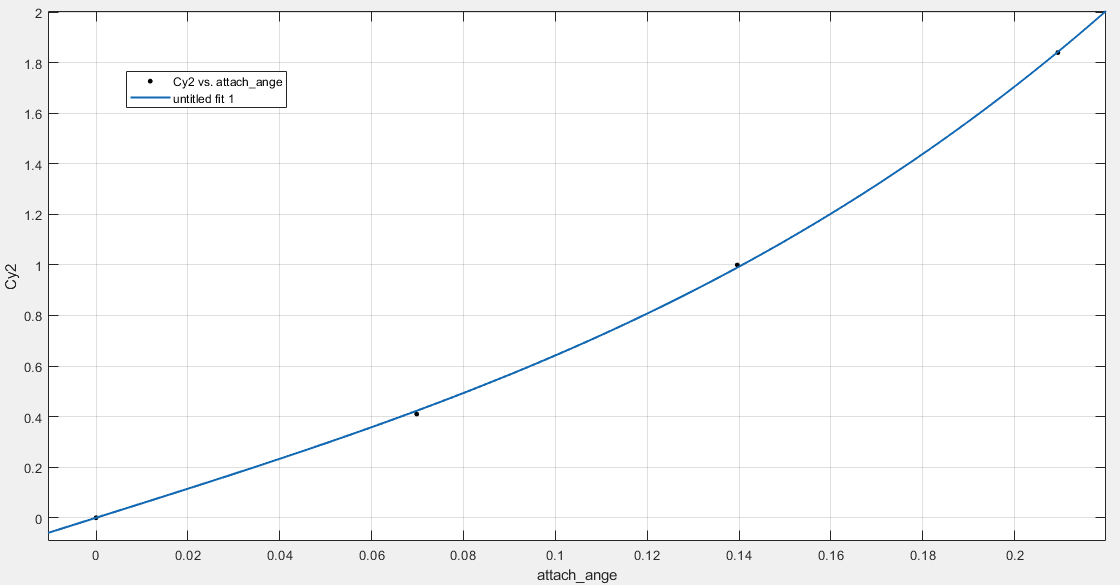 Рис.3. «График зависимости Рис.3. «График зависимости 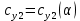 » »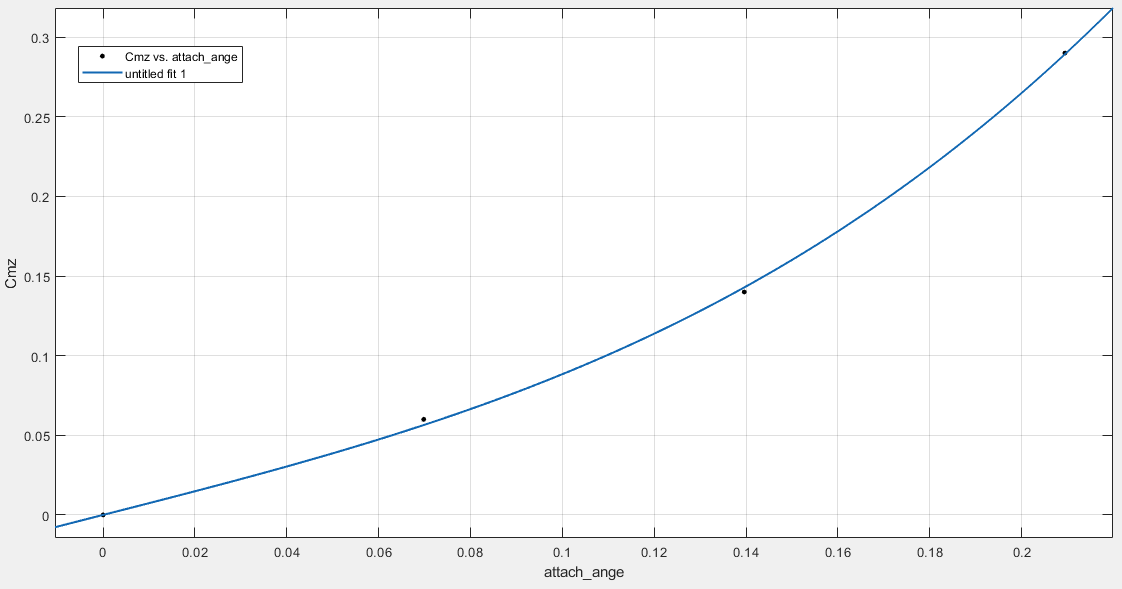 Рис.4. «График зависимости Рис.4. «График зависимости 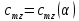 » »Вывод: Из графиков зависимости аэродинамических коэффициентов cx, cy и cmz по отношению к изменению угла атаки мы наблюдаем положительную экспоненциальную зависимость, с увеличением угла атаки 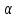 наблюдается увеличение значения аэродинамических коэффициентов cx, cy и cmz. наблюдается увеличение значения аэродинамических коэффициентов cx, cy и cmz. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
