Водно-технические изыскания. Лабораторная работа 1 Определение нормы годового стока и расчёт среднегодовых расходов различной обеспеченности
 Скачать 83.28 Kb. Скачать 83.28 Kb.
|
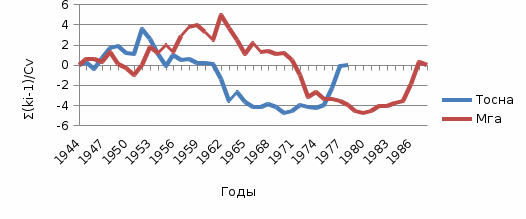 Рисунок 3 – Разностная интегральная кривая среднегодовых расходов воды реки-аналога и расчётной реки. Как правило, многоводные и маловодные годы чередуются, это приводит к образованию циклов водности. Чтобы оценить цикл водности необходимо посчитать средний модульный коэффициент: 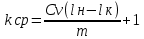 (4) (4)В нашем случае kср = 0,996. Это значение близко к 1, то есть наш цикл средний по водности. За имеющийся период наблюдений водность расчётной реки была на 1% ниже нормы. Построение графика связи среднегодовых расходов воды расчетной реки и реки-аналога строится по данным сразу двух рек, где по оси у – расходы расчётной реки, а по оси х – расходы реки-аналога. 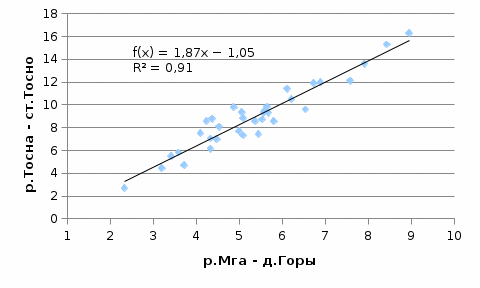 Рисунок 4 – График связи среднегодовых расходов воды р.Мга – д.Горы и р.Тосна – ст.Тосно Таблица 7 – Параметры уравнения линейной регрессии.
Уравнение регрессии является надёжным, потому что выполняются следующие условия: n = 34; R = 0,95; R/σR = 59; a/σa = 17 Так как все условия выполнены, то уравнение можно использовать для дальнейших расчётов. По полученному уравнению регрессии можно посчитать норму стока на расчётной реке, приведённую к длинному ряду реки-аналога: 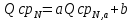 (5) (5)В данном случае QсрN = 9,02 Оценить погрешность расчёта нормы стока, приведенной к длинному ряду реки-аналога можно по формуле: 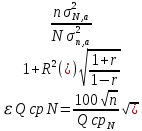 (6) (6)В данном случае ɛQсрN = 8,82 Расчёт нормы годового стока при отсутствии данных гидрометрических наблюдений. При отсутствии данных наблюдений используют способ интерполяции. В данной работе норма стока определяется только по одной реке-аналогу. То есть предполагается, что средние многолетние модули стока на расчётной реке примерно одинаковы с рекой-аналогом. Расчёт производится по формуле: 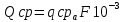 (7) (7)Где qсра – средний многолетний модуль стока реки-аналога; F – площадь водосбора расчётной реки. В данном примере Qср = 5,38 м3/с В данной части работы наименьшую погрешность даёт метод, когда имеются все данные гидрометрических наблюдений. 2.1 Расчёт среднегодовых расходов воды различной обеспеченности при наличии данных гидрометрических наблюдений Требуется рассчитать среднегодовые расходы по заданной обеспеченности, при этом предполагается, что используемые ряды являются однородными. По формулам (8-10) рассчитывается коэффициент вариации, коэффициент ассиметрии и средний расход: 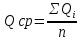 ; ; 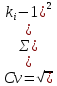 ; ; 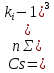 (8-10) (8-10)Таблица 8 – Параметры распределения расчётной реки и реки-аналога и их погрешности.
Учитывая, что погрешность коэффициента ассиметрии существенно превышает допустимую в качестве расчетного значения (Cs/Cv) принимается 1. С использованием полученных значений по соответствующим таблицам определяются ординаты аналитических кривых обеспеченностей Крицкого-Менкеля. Таблица 9 – Ординаты аналитической кривой обеспеченностей Крицкого-Менкеля для среднегодовых расходов воды расчётной реки.
Таблица 10 – Ординаты аналитической кривой обеспеченностей Крицкого-Менкеля для среднегодовых расходов реки-аналога.
Расчёт эмпирической обеспеченности производится по формуле: 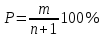 (11) (11)Таблица 11 – Расчёт ординат эмпирической кривой обеспеченностей среднегодовых расходов реки-аналога.
Продолжение таблицы 11
Таблица 12 – Расчёт ординат эмпирической кривой обеспеченностей среднегодовых расходов расчётной реки.
Продолжение таблицы 12
Так как аналитические кривые хорошо согласуются с эмпирическими точками, то расходы, представленные в таблицах 9 и 10 можно рекомендовать в качестве расчётных. 2.2 Расчёт среднегодовых расходов воды различной обеспеченности при недостаточности данных гидрометрических наблюдений. По формуле (5) QсрN = 5,35 м3/с | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
