Математический маятник. Лабораторная работа 1 Определение периода колебаний маятника
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Лабораторная работа №1 Определение периода колебаний маятника Цель работы: Изучить колебательное движение нитяного маятника и определить его период и частоту, выяснить как эти характеристики зависят от длины маятника. ОБЩИЕ СВЕДЕНИЯ В повседневной жизни мы достаточно часто наблюдаем колебательные процессы. Это смена дня и ночи, вращение Луны вокруг Земли, вибрация струн у музыкальных инструментов, колебания маятника часов и т.д. В колебательном движение изменение какой-либо величины (например, скорости или смещения тела от положения равновесия) повторяется в точности через совершенно определенное время - период. Рассмотрим колебания нитяного маятника, т.е. небольшого тела (например, шарика), подвешенного на нити, длина которой значительно превышает размеры самого тела. Если шарик отклонить от положения равновесия и отпустить, то он начнет колебаться. Сначала маятник движется с нарастающей скоростью вниз. В положении равновесия скорость шарика не равна нулю, и он по инерции движется вверх. По достижении наивысшего положения шарик снова начинает двигаться вверх. Колебательное движение характеризуют амплитудой, периодом и частотой колебаний. Период - это время, за которое тело совершает одно колебание. Частота - это число колебаний, совершаемых за единицу времени. ЭКСПЕРЕМЕНТАЛЬНАЯ ЧАСТЬ ПРИБОРЫ 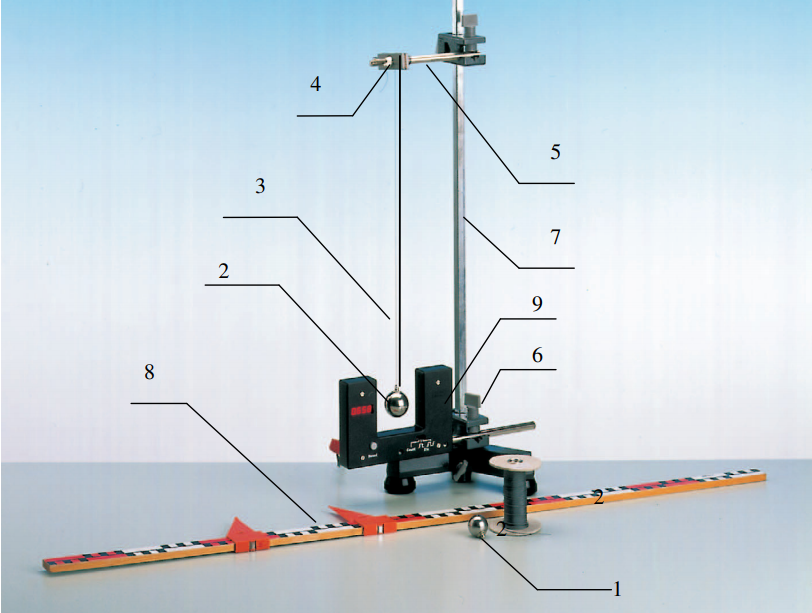 1 - стальной шарик массой m1= 68 г (D=24,4 мм); 2 - стальной шарик массой m2 =135 г (D=32 мм); 3 - нить; 4 - регулятор длины нити; 5 - верхний кронштейн; 6 - нижний кронштейн; 7 - штатив; 8 – измерительная линейка с двумя передвижными указателями (L=1000 мм); 9 - счетчик колебаний. ПОРЯДОК ВЫПОЛНЕНИЯ 1. Для малых отклонений, определить период колебаний как функцию длины нити; 2. Определить величину ускорения свободного падения; 3. Экспериментально проверить влияние массы шарика на период колебания. 4.1. Стальной шарик за специальное отверстие подвесить на нити , нить закрепить в верхнем кронштейне . 4.2. Установить верхний кронштейн на расстоянии 120 см от нижнего кронштейна. 4.3. Счетчик колебаний установить в нижнем кронштейне и зафиксировать его. 4.4. Вращая регулятор длины нити на верхнем кронштейне установить маятник так, чтобы шарик пересекал уровень фотоэлектрического датчика. 4.5. Для измерения периода колебаний переключатель режимов работы счетчика установить в крайнее правое положение (на дисплее высвечиваются четыре светящиеся точки). 4.6. Отклонить шарик от положения равновесия на небольшой угол (3-50 ) и отпустить его. Определить период колебаний маятника T1 . Результат записать в таблицу. 4.7. Затем, отклонив шарик от положения равновесия на тот же угол, но в другую сторону и отпустив его, определить период колебаний маятника T2 . Результат также записать в таблицу. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ. АНАЛИЗ И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ. 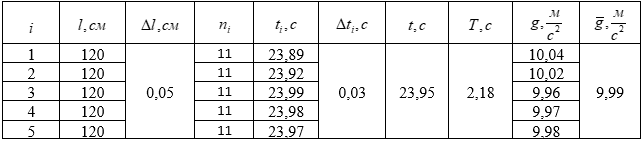 ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ Что представляет собой математический маятник? Осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения. Другой конец нити обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Какой вид имеет выражение для периода колебаний математического маятника? 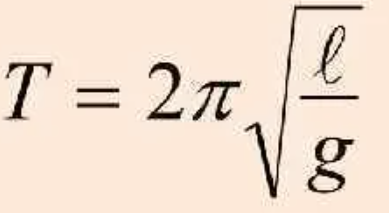 Какие колебания называются гармоническими? Гармоническими колебаниями называются колебания, в которых изменение какой-либо физической величины происходит по закону синуса или косинуса. Что такое период колебаний? Наименьший промежуток времени, за который система совершает одно полное колебание. В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени. 5. Что такое частота колебаний? Частота - это физическая величина обратная периоду колебаний (T). Частота - это число полных колебаний, которые совершаются за единицу времени. |
