вариант_ Обработка результатов. Лабораторная работа 1 Определение плотности материала пластины

• Название: Лабораторная работа 1 Определение плотности материала пластины
• Дата: 24.11.2020
• Размер: 203.5 Kb.
• Имя файла: вариант_ Обработка результатов.doc
• Тип: Лабораторная работа; #153493

Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Омский государственный технический университет»

Обработка результатов измерений
Методические указания

Омск 2019

Лабораторная работа № 1

Определение плотности материала пластины

Определение номера варианта к лабораторной работе №1

Номер задания определяется по таблице 3 по двум последним цифрам номера зачетной книжки (студенческого билета). Если число, образованное этими цифрами, меньше или равно 24, то это и есть номер задания. Если число, образованное этими цифрами, больше 24, то из него нужно вычитать 24 столько раз, пока не останется число меньшее или равное 24, и оно определяет номер задания.
Таблица 3

№	Масса m, г	Длина li, мм	Ширина bi, мм	Толщина hi, мм
1	72,9	49,6	29,4	5,7
		49,5	29,3	5,6
		49,6	29,3	5,6
2	68,8	49,6	29,4	5,7
		49,5	29,3	5,6
		49,6	29,3	5,6
3	63,1	49,6	29,4	5,7
		49,5	29,3	5,6
		49,6	29,3	5,6
4	22,1	49,6	29,4	5,7
		49,5	29,3	5,6
		49,6	29,3	5,6
5	72,5	48,2	39,9	4,2
		48,2	40,0	4,2
		48,1	39,9	4,3
6	68,4	48,2	39,9	4,2
		48,2	40,0	4,2
		48,1	39,9	4,3
7	62,7	48,2	39,9	4,2
		48,2	40,0	4,2
		48,1	39,9	4,3
8	22,0	48,2	39,9	4,2
		48,2	40,0	4,2
		48,1	39,9	4,3
9	30,4	37,4	30,2	3,0
		37,4	30,1	3,0
		37,2	30,2	3,0
10	28,7	37,4	30,2	3,0
		37,4	30,1	3,0
		37,2	30,2	3,0
11	26,3	37,4	30,2	3,0
		37,4	30,1	3,0
		37,2	30,2	3,0
12	9,2	37,4	30,2	3,0
		37,4	30,1	3,0
		37,2	30,2	3,0
13	45,5	50,5	48,6	2,1
		50,4	48,7	2,1
		50,4	48,7	2,0
14	43,0	50,5	48,6	2,1
		50,4	48,7	2,1
		50,4	48,7	2,0
15	39,4	50,5	48,6	2,1
		50,4	48,7	2,1
		50,4	48,7	2,0
16	13,8	50,5	48,6	2,1
		50,4	48,7	2,1
		50,4	48,7	2,0
17	81,6	55,3	29,5	5.7
		55,2	29,4	5,6
		55,1	29,3	5,7
18	77,0	55,3	29,5	5.7
		55,2	29,4	5,6
		55,1	29,3	5,7
19	70,6	55,3	29,5	5.7
		55,2	29,4	5,6
		55,1	29,3	5,7
20	24,8	55,3	29,5	5.7
		55,2	29,4	5,6
		55,1	29,3	5,7
21	24,5	30.0	29,8	3,0
		30,1	29,9	3,1
		30,1	29,7	3,1
22	23,1	30.0	29,8	3,0
		30,1	29,9	3,1
		30,1	29,7	3,1
23	21,2	30.0	29,8	3,0
		30,1	29,9	3,1
		30,1	29,7	3,1
24	7,4	30.0	29,8	3,0
		30,1	29,9	3,1
		30,1	29,7	3,1

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Все проводимые измерения можно разделить на прямые и косвенные. а) При прямых измерениях искомая величина получается непосредственно при помощи измерительного прибора. Так называемая приборная погрешность определяется при этом по классу точности прибора, а если он не указан, то приборная погрешность принимается равной половине цены наименьшего деления шкалы прибора.

б) При косвенных измерениях искомая величина y не измеряется, а вычисляется по формуле через другие, непосредственно измеряемые величины x₁, x₂,…x_n, то есть, измеряемая величина является некоторой функцией одного или нескольких аргументов y = y( x_1,x_2,…x_n ).

Косвенные измерения являются воспроизводимыми, если каждый аргумент при повторении измерений должен принимать одно и то же значение.

Косвенные измерения являются невоспроизводимыми, если при повторении измерений аргументы принимают заведомо разные значения.

1. 
   Последовательность обработки результатов при прямых измерениях
   

1.1. Определить приборную погрешность .

1.2. Провести измерения n раз некоторой величины , определив значения .

1.3. Вычислить среднее арифметическое значение результатов измерений

.

1.4. Определить величины отклонений результатов измерений от среднего значения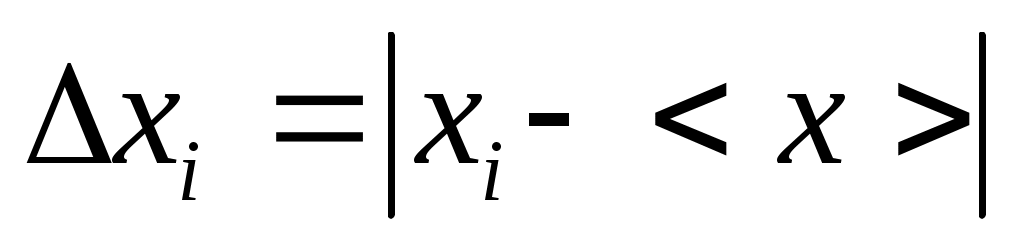

.

1.5. Рассчитать среднеквадратичную погрешность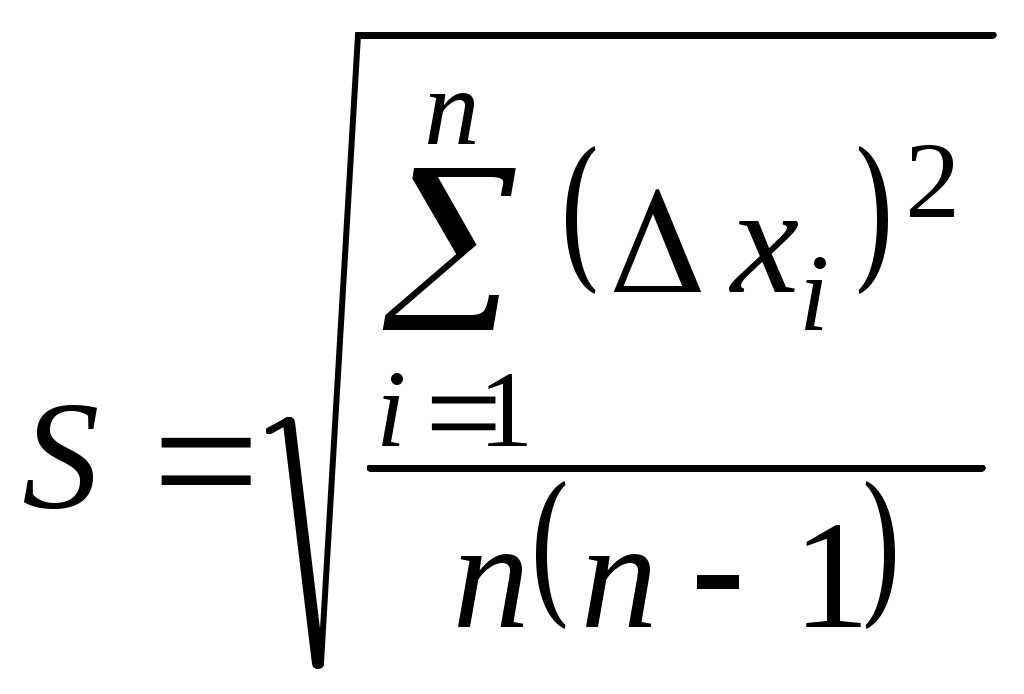

.

1.6. Задать величину надежности измерений a и по таблице найти значение коэффициента Стьюдента .

1.7. Найти случайную погрешность измерений

.

1.8. Вычислить абсолютную погрешность измерений

.

1.9. Вычислить значение относительной погрешности измерений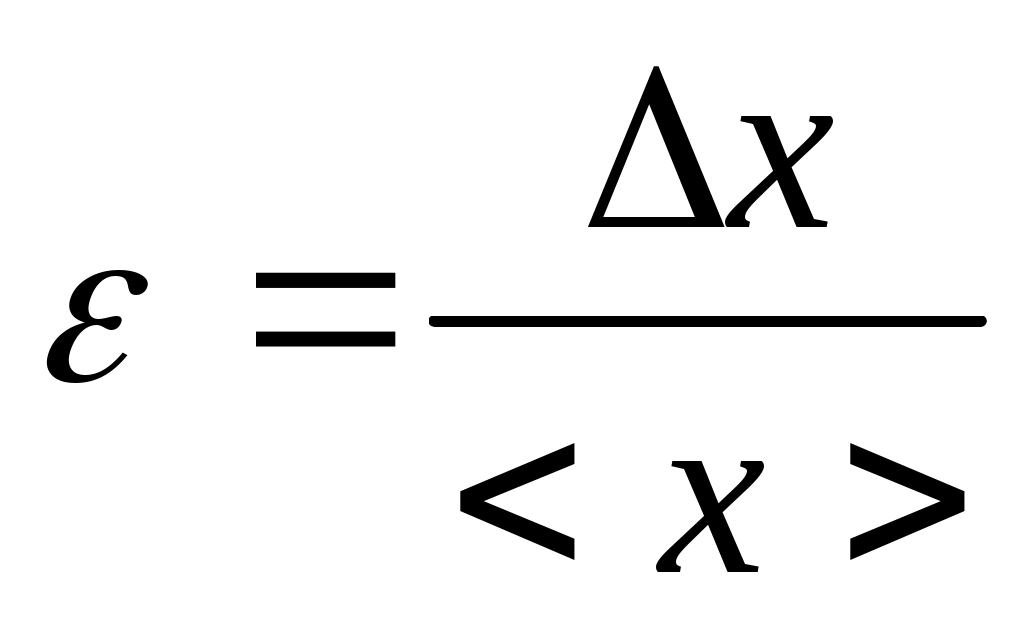

.

1.10. Записать результат обработки данных в виде: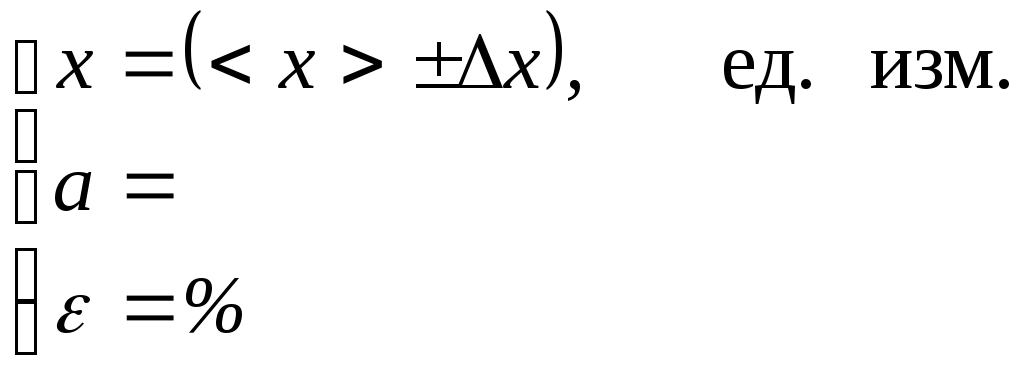


При записи окончательного результата абсолютная погрешность измерений округляется до двух первых значащих цифр, если первая меньше или равна 3, или до одной значащей цифры, если первая больше 3. Погрешность округляется в сторону увеличения.

Числовое значение определяемой величины должно оканчиваться цифрой того же разряда, что и значение абсолютной погрешности.

Относительная погрешность округляется до двух значащих цифр в сторону увеличения.
Таблица значений коэффициента Стьюдента

α/n	2	3	4	5	6	7	8	9	10	11
0,7	2,0	1,3	1,3	1,2	1,2	1,1	1,1	1,1	1,1	1,0
0,8	3,08	1,89	1,64	1,53	1,48	1,44	1,42	1,4	1,38	2,28
0,9	6,31	2,92	2,35	2,13	2,02	1,94	1,9	1,86	1,83	1,64
0,95	12,7	4,3	3,18	2,78	2,57	2,45	2,36	2,31	2,26	1,96

2. Последовательность обработки результатов

при косвенных воспроизводимых измерениях
2.1. Произвести прямые измерения величин и обработать данные как для прямых измерений.

2.2. Вычислить искомую величину один раз, подставив в расчетную формулу средние значения непосредственно измеряемых величин .

2.3. Вывести формулу для расчета 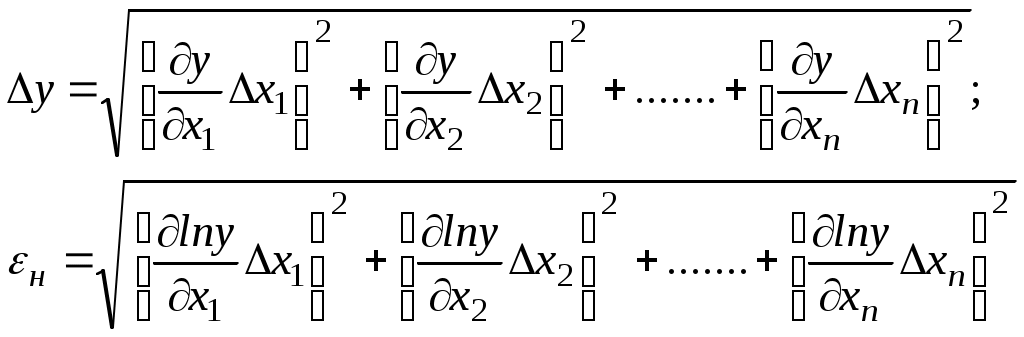или



2.4. Вычислить абсолютную и относительную погрешности измерений.

2.5. Произвести округление результатов и записать окончательный ответ по аналогии с пунктом 1.10.

Примечания:

1. 
   Абсолютные погрешности всех аргументов рассчитываются при одном и том же значении надежности.
   
2. 
   Если в расчетную формулу для искомой величины y входят величины, которые не измеряются в процессе выполнения работы (заранее заданы) и для них не указана величина погрешности, то за погрешность таких величин принимают половину единицы наименьшего разряда, представленного в заданном числе.
   
3. 
   Если в расчетную формулу для искомой величины y входят величины, округляемые при проведении расчетов ( g, π и т.д.), то их тоже надо считать аргументами, принимая за погрешность величину округления.
   

3. Последовательность обработки результатов

при косвенных невоспроизводимых измерениях

3.1. Произвести прямые измерения величин n раз, где k– номер измеряемой величины, приписываемый аргументам , от которых зависит функция y.

.

3.2. Рассчитать n значений искомой величины



подставив в формулу вместо , где i – номер измерения величины .

3.3. Вычислить среднее значение



3.4. Найти отклонение значений 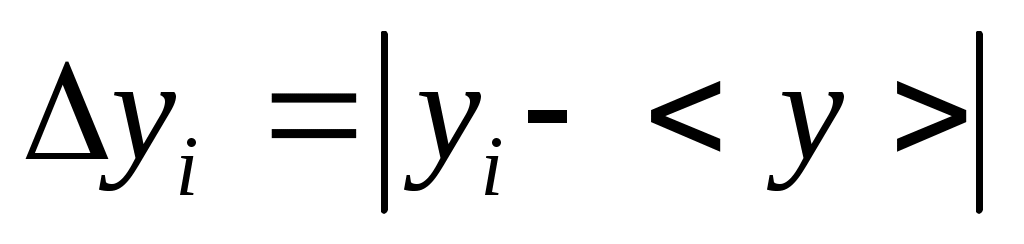от среднего значения:

.

3.5. Определить среднеквадратичную погрешность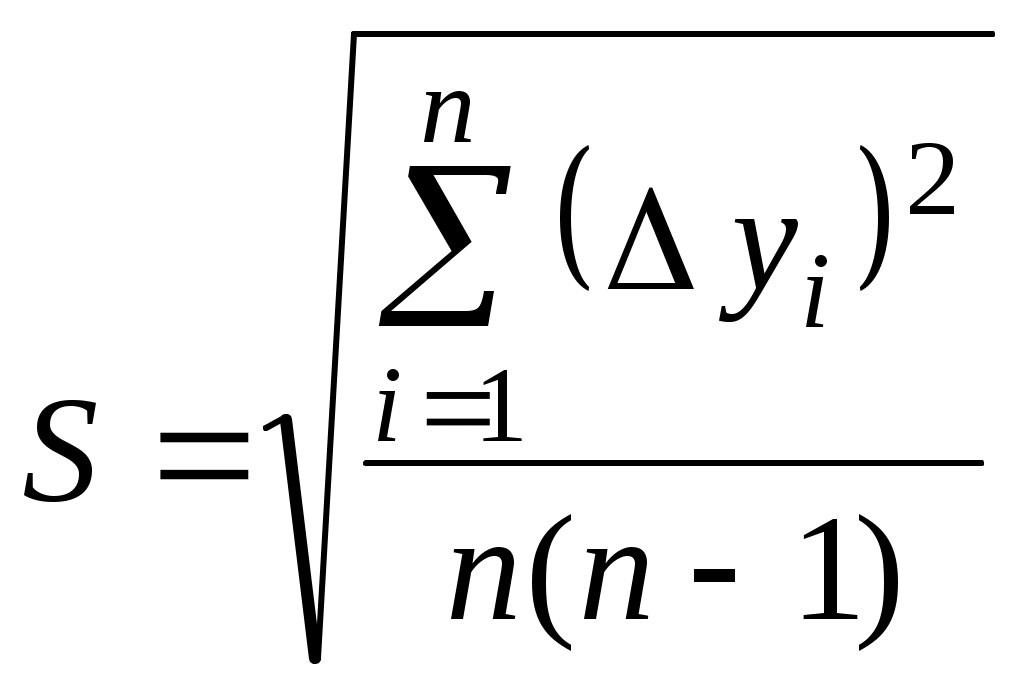

.

3.6. Задать значение надежности измерения и по таблице найти коэффициент Стьюдента .

3.7. Найти случайную погрешность измерений

.

3.8. Приняв за величину абсолютной погрешности измерений случайную погрешность, вычислить относительную погрешность



3.9 Записать окончательный результат по аналогии с пунктом 1.10.