Лабораторная работа 1 По дисциплине Физика Выполнил Трубина А. А. Группа мб12
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов Лабораторная работа №1 По дисциплине: ФизикаВыполнил: Трубина А.А. Группа: МБ-12 Вариант: 2 Проверил: Стрельцов А.И. Новосибирск, 2021 г. Лабораторная работа № 1. «Изучение характеристик электростатического поля». Цель работы: Изобразить графически сечение эквипотенциальных поверхностей электростатического поля, созданного заданной конфигурацией электрических зарядов, используя изображение эквипотенциальных поверхностей, построить силовые линии электростатического поля заданной конфигурации зарядов. При помощи полученной картины силовых и эквипотенциальных линий проверить справедливость формулы связи напряжённости электрического поля с его потенциалом. Основные теоретические сведения. Помимо механического взаимодействия тел в природе существуют и другие фундаментальные виды взаимодействия. Тела, способные к таким взаимодействиям, обладают особыми физическими свойствами. Одним из таких свойств является электрический заряд. Обладающие электрическим зарядом тела способны вступать в новый вид взаимодействия, который называется электрическим (точнее – электромагнитным) взаимодействием. Электрический заряд не может существовать без материального носителя. Электромагнитное взаимодействие превосходит механическое по интенсивности примерно на 40 порядков. Кроме того, электромагнитное взаимодействие может носить не только характер притяжения, но и характер отталкивания. Установлено, что в природе существует два вида электрических зарядов, один из которых условно был назван положительным, другой – отрицательным. Эксперименты показывают, что одинаковые по знаку электрические заряды отталкиваются, а противоположного знака – притягиваются. Электрический заряд обладает свойством сохранения: в замкнутой системе алгебраическая сумма электрических зарядов остается неизменной при любых взаимодействиях тел внутри такой системы. Это утверждение получило название закона сохранения электрического заряда. Кроме того, заряд обладает свойством делимости: его можно распределять между телами. Однако, существует предельное значение величины заряда, дальше которой он уже не делится. Было обнаружено, что такой минимальный заряд неразрывно связан с очень маленькой частицей, которая была названа электроном. Заряд электрона оказался равным  иусловно считается отрицательным. иусловно считается отрицательным.Электрический заряд обозначается буквой  и измеряется в кулонах (Кл). Единица заряда названа в честь французского физика Шарля Огюстена Кулона, впервые количественно охарактеризовавшего электромагнитное взаимодействие. и измеряется в кулонах (Кл). Единица заряда названа в честь французского физика Шарля Огюстена Кулона, впервые количественно охарактеризовавшего электромагнитное взаимодействие.Действие одного электрически заряженного тела на другое осуществляется посредством электромагнитного поля.Электромагнитное поле – это структурная форма материи, посредством которой осуществляется электромагнитное взаимодействие. Основные свойства этого силового поля таковы: - Электромагнитное поле создается только электрически заряженными телами (электрическими зарядами). Если электрические заряды, создающие поле, неподвижны в заданной системе отсчета, то создаваемое поле называется электростатическим. - Электромагнитное поле способно оказывать силовое воздействие на помещенный в него электрический заряд. - Поле является объективной реальностью, то есть, его существование не зависит от наших знаний о нем. Обладая достаточными знаниями, мы можем создать приборы, способные обнаружить и использовать это поле. Силовое воздействие электростатического поля на электрический заряд количественно характеризуется законом Кулона: сила взаимодействия двух точечных неподвижных зарядов пропорциональна величине заряда, создающего поле, величине заряда, помещенного в это поле и обратно пропорциональна квадрату расстояния между зарядами.  (1) (1)где  - сила взаимодействия заряда с полем, - сила взаимодействия заряда с полем,  - коэффициент пропорциональности, обусловленный выбором системы единиц СИ, - коэффициент пропорциональности, обусловленный выбором системы единиц СИ, 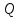 - величина заряда, создающего поле, - величина заряда, создающего поле,  - величина заряда, помещенного в поле, - величина заряда, помещенного в поле,  - расстояние между зарядами, - расстояние между зарядами,  - относительная диэлектрическая проницаемость среды, заполняющей пространство между зарядами, - относительная диэлектрическая проницаемость среды, заполняющей пространство между зарядами,  - электрическая постоянная. - электрическая постоянная.Сила взаимодействия электрических зарядов (сила Кулона) направлена вдоль прямой, проходящей через центры взаимодействующих электрических зарядов, то есть, является центральной силой. В векторном виде закон Кулона можно записать так:  (2) (2)Вектор  имеет единичную величину и направление, совпадающее с направлением координатной оси, соединяющей центры взаимодействующих зарядов. имеет единичную величину и направление, совпадающее с направлением координатной оси, соединяющей центры взаимодействующих зарядов.Названия зарядов «создающий поле» и «помещённый в поле» полностью условны; их можно легко менять местами. Правильный выбор роли каждого заряда часто облегчает решение задачи. Электростатическое поле в каждой точке пространства характеризуется двумя параметрами: напряжённостью и потенциалом. Напряжённость электрического поля – это физическая величина, равная силе, действующей на положительный единичный точечный заряд, помещённый в данную точку поля.  (3) (3)Из определения напряжённости следует, что сила, действующая со стороны электрического поля на точечный заряд, равна:  (4) (4)Единица напряжённости электрического поля в системе СИ -  . .Исходя из закона Кулона (1) и определения (3), можно рассчитать напряжённость электрического поля, создаваемого одиночным точечным зарядом в вакууме:  (5) (5)Для расчета напряжённости электрического поля, создаваемой заряженными телами произвольной формы, используется теорема Гаусса: поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность, содержащую электрические заряды, равен отношению алгебраической суммы этих зарядов к электрической постоянной и диэлектрической проницаемости среды, которой заполнено пространство внутри поверхности.  (6) (6)Значение теоремы заключается в том, что с её помощью можно рассчитать электрическое поле, создаваемое сколь угодно сложной конфигурацией электрических зарядов. По известному из курса механики принципу независимости действия сил, результирующее значение напряжённости поля, создаваемого одновременно несколькими электрическими зарядами в одной и той же точке пространства, определяется согласно принципу суперпозиции: результирующая напряжённость электрического поля равна векторной сумме напряжённостей полей, создаваемых каждым из имеющихся зарядов:  (7) (7)Электрическое поле характеризуется также потенциалом - энергетической величиной, равной потенциальной энергии положительного единичного точечного заряда, помещенного в данную точку поля:  (8) (8)где  - потенциал, - потенциал,  - потенциальная энергия взаимодействия электрического заряда с полем, - потенциальная энергия взаимодействия электрического заряда с полем,  - величина этого заряда. Размерность потенциала в системе единиц СИ: - величина этого заряда. Размерность потенциала в системе единиц СИ:  . .Потенциал поля, создаваемого одиночным точечным зарядом в вакууме, равен  (9) (9)Результирующее значение потенциала, создаваемого одновременно несколькими электрическими зарядами в одной и той же точке пространства, определяется согласно принципу суперпозиции:результирующий потенциал электрического поля равен алгебраической сумме потенциалов полей, создаваемых каждым из имеющихся зарядов:  (10) (10)Потенциал - скалярная величина, которая определяется с точностью до произвольной постоянной. Поэтому физический смысл имеет только разность потенциалов. Разность потенциалов связана с работой сил электрического поля по перемещению точечного заряда следующим образом: 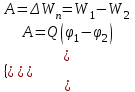 (11) (11)где  - потенциалы начальной и конечной точек положения заряда. Введение понятий потенциала и потенциальной энергии заряда в электрическом поле связано с тем, что работа по перемещению заряда в электрическом поле не зависит от траектории его движения, а определяется лишь начальным и конечным положением заряда. В соответствие с (11) эта работа определяется разностью потенциалов начальной и конечной точек. - потенциалы начальной и конечной точек положения заряда. Введение понятий потенциала и потенциальной энергии заряда в электрическом поле связано с тем, что работа по перемещению заряда в электрическом поле не зависит от траектории его движения, а определяется лишь начальным и конечным положением заряда. В соответствие с (11) эта работа определяется разностью потенциалов начальной и конечной точек.Напряжённость и потенциал - два физических параметра одного и того же объекта – электрического поля. Для нахождения связи между ними рассчитаем работу при бесконечно малом перемещении точечного заряда в электрическом поле из точки 0 в точку А (рисунок 1). Элементарная механическая работа при таком перемещении вычисляется так: 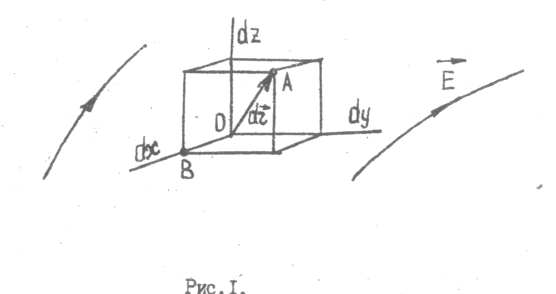  (12) (12)В соответствие с формулой (11) эта же работа равна: 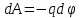 (13) (13)Рисунок 1. К расчёту связи напряжённости электрического поля с его потенциалом Сопоставляя формулы (13) и (12) и учитывая явное выражение для силы (4), получим  (14) (14)Переместим теперь заряд из точки  в точку в точку  на расстояние на расстояние  при фиксированных значениях координат при фиксированных значениях координат  и и   . В соответствии с формулой (13) получим: . В соответствии с формулой (13) получим: (15) (15)где  - проекция вектора напряжённости на ось - проекция вектора напряжённости на ось  . Последнюю формулу перепишем так: . Последнюю формулу перепишем так:  (16) (16)где частная производная находится путем дифференцирования потенциала по координате  при фиксированных значениях при фиксированных значениях  и и  . По аналогии можно получить выражения для проекции вектора напряжённости на другие оси координат: . По аналогии можно получить выражения для проекции вектора напряжённости на другие оси координат: (17) (17) (18) (18)Из полученных проекций легко сформировать вектор напряжённости электрического поля  (19) (19)Выражение в скобках называется градиентом потенциала и сокращённо записывается так:  или или  (20) (20)Градиент скалярной функции - это вектор, характеризующий скорость пространственного изменения функции и направленный в сторону максимального её возрастания. Как видно из формулы (20), вектор напряжённости электрического поля направлен в сторону, противоположную максимальному возрастанию потенциала. Основной целью лабораторной работы является экспериментальная проверка справедливости этой формулы. Во многих практических задачах требуется знание напряжённости электрического поля. Однако легче рассчитать скалярную величину - потенциал, а затем по формуле (20) вычислить вектор напряжённости электрического поля.  Формула (19) упрощается, если электрическое поле обладает аксиальной или центральной симметрией: 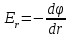 (21) (21)Рисунок 2. Силовые линии электрического поля где  показывает направление изменения электрического поля. При небольших расстояниях между исследуемыми точками возможно перейти от дифференцирования к конечным приращениям: показывает направление изменения электрического поля. При небольших расстояниях между исследуемыми точками возможно перейти от дифференцирования к конечным приращениям: (22) (22)где x1,x2 – координаты двух точек, лежащих на силовой линии; φ1, φ2 – потенциалы этих точек. Электростатическое поле удобно изображать графически с помощью силовых линий и эквипотенциальных поверхностей. Силовая линия электростатического поля – это геометрическая кривая, в каждой точке которой вектор напряжённости электрического поля направлен к ней по касательной (рисунок 2). Принято считать, что силовая линия начинается на положительных и заканчивается на отрицательных электрических зарядах. Число силовых линий, приходящихся на единичную перпендикулярную к ним площадь поверхности, характеризует абсолютную величину напряжённости поля: чем гуще расположены силовые линии, тем больше величина напряжённости поля. На рисунке 2 напряжённость поля в точке (1) больше, чем в точке (2) или (3).  Рисунок 3. Силовые линии однородного электрического поля Если силовые линии электрического поля представляют собой параллельные прямые, расположенные на равных расстояниях между собой, и направленные в одну и ту же сторону, то такое поле называется однородным (рисунок 3). Примером такого поля может являться поле, создаваемое большой равномерно заряженной плоскостью. Нарушение хотя бы одного из перечисленных условий делает электрическое поле неоднородным (рисунок 2). Эквипотенциальные поверхности – это поверхности, во всех точках которых потенциал имеет одно и то же значение. Эти поверхности целесообразно проводить так, чтобы разность потенциалов между соседними поверхностями была одинаковой (рисунок 4). На плоскости поверхности превращаются в эквипотенциальные линии.  Рисунок 4. Эквипотенциальные поверхности поля заряженного шара  Рисунок 5. К доказательству взаимной перпендикулярности силовых и эквипотенциальных линий Покажем, что в каждой точке пространства вектор напряжённости электрического поля 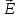 перпендикулярен эквипотенциальной поверхности и направлен в сторону уменьшения потенциала. Для этого рассчитаем работу по перемещению заряда перпендикулярен эквипотенциальной поверхности и направлен в сторону уменьшения потенциала. Для этого рассчитаем работу по перемещению заряда 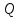 вдоль эквипотенциальной поверхности на бесконечно малое расстояние вдоль эквипотенциальной поверхности на бесконечно малое расстояние 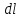 (рисунок 6). (рисунок 6). Такая работа равна нулю, поскольку определяется разностью потенциалов точек 1 и 2. С другой стороны, в соответствии с (4) и (12), работа записывается так: 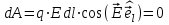 (23) (23)где 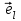 - единичный вектор, направленный по касательной к эквипотенциальной поверхности. Из формулы (22) следует, что косинус угла между векторами - единичный вектор, направленный по касательной к эквипотенциальной поверхности. Из формулы (22) следует, что косинус угла между векторами 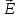 и и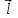 равен нулю и вектор равен нулю и вектор 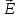 перпендикулярен эквипотенциальной поверхности. Далее переместимся по нормали перпендикулярен эквипотенциальной поверхности. Далее переместимся по нормали  к эквипотенциальной поверхности в сторону уменьшения потенциала. В этом случае к эквипотенциальной поверхности в сторону уменьшения потенциала. В этом случае  и из формулы (21) следует, что и из формулы (21) следует, что 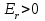 . Значит, вектор . Значит, вектор 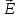 направлен по нормали в сторону уменьшения потенциала. направлен по нормали в сторону уменьшения потенциала. |
