Лабораторная работа 1 По дисциплине Физика Выполнил Трубина А. А. Группа мб12
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Контрольные вопросы Электрическое поле, его основные физические свойства. Электростатическое поле. Электрическое поле – это структурная форма материи, посредством которой осуществляется электрические взаимодействие. Основные свойства этого силового поля таковы: Электрическое поле создается только электрически заряженными телами (электрическими зарядами). Если электрические заряды, создающие поле, неподвижны в заданной системе отсчета, то создаваемое поле называется электростатическим. Электромагнитное поле способно оказывать силовое воздействие на помещенный в него электрический заряд. Поле является объективной реальностью, то есть, его существование не зависит от наших знаний о нем. Обладая достаточными знаниями, мы можем создать приборы, способные обнаружить и использовать это поле. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга. Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля. Основные характеристики электростатического поля: - напряженность - потенциал Силовые линии электростатического поля имеют следующие свойства: - Всегда незамкнуты: начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности). - Не пересекаются и не касаются друг друга. - Густота линий тем больше, чем больше напряжённость, то есть напряжённость поля прямо пропорциональна количеству силовых линий, проходящих через площадку единичной площади, расположенную перпендикулярно линиям. Основные параметры электрического поля: напряжённость и потенциал, связь между ними (с выводом). Основные характеристики электростатического поля: - напряженность - потенциал Напряжённость электрическогополя — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы Единица измерения напряженности электрического поля - В/м. Электростатический потенциал – скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещенный в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт, 1 В = 1 Дж/Кл. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда: Напряженность электростатического поля Е и потенциал 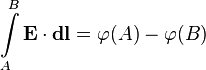 Или обратно Здесь Ошибка! Любую из выделенных формул необходимо вывести. Если пробный заряд q совершил малое перемещение Δ 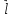 вдоль силовой линии из точки (1) в точку (2), то можно записать:
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует выражение
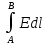 = - (φB – φA) = φA - φB = - (φB – φA) = φA - φBЭто соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии. Для трехмерного поля вектор напряженности электростатического поля в этом случае необходимо записать как 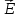 = = 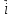 Ex + Ex +  Ey + Ey + 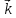 Ez EzВ соответствии с формулой 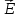 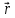 = - d ϕ = - d ϕ получим: Exdx = - d ϕ где Ex- проекция вектора напряжённости на ось X Ex = - 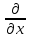 ϕ ϕгде частная производная находится путем дифференцирования потенциала по координате x при фиксированных значениях y и z . По аналогии можно получить выражения для проекции вектора напряжённости на другие оси координат: Ey = - 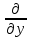 ϕ, Ez = - ϕ, Ez = - 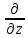 ϕ ϕВ результате вектор напряжённости электрического поля 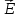 = - ( = - ( 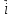 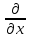 ϕ + ϕ +  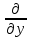 ϕ + ϕ + 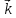 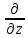 ϕ ) ϕ ) Выражение в скобках есть градиент потенциала и сокращённо записывается так: 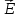 = - = - 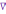 ϕ ϕили 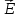 = - grad ϕ (1) = - grad ϕ (1)Градиент скалярной функции - это вектор, характеризующий скорость пространственного изменения функции и направленный в сторону максимального её возрастания. Как видно из формулы (1) , вектор напряжённости электрического поля направлен в сторону, противоположную максимальному возрастанию потенциала Потенциал электрического поля, разность потенциалов, электрическое напряжение. Связь между этими физическими величинами. Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля: Потенциал φ является энергетической характеристикой электростатического поля. Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек: A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2) Разность потенциалов φ1 – φ2 называется напряжением между точками 1 и 2 и обозначается U12 или просто U U = А/q = φ1 – φ2 Напряжение между двумя точками поля численно равно работе сил поля по перемещению единичного заряда q между этими точками. Ошибка! Разность потенциалов и напряжение – это разные физические величины. Установите связь между этими величинами для случая однородного и неоднородного электрических полей. Выясните, когда эти величины равны по модулю и объясните, почему они противоположны по знаку. Разность потенциалов связана с работой сил электрического поля по перемещению точечного заряда следующим образом: 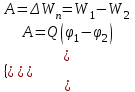 где  - потенциалы начальной и конечной точек положения заряда. Работа по перемещению заряда в электрическом поле не зависит от траектории его движения, а определяется лишь начальным и конечным положением заряда, работа определяется разностью потенциалов начальной и конечной точек. - потенциалы начальной и конечной точек положения заряда. Работа по перемещению заряда в электрическом поле не зависит от траектории его движения, а определяется лишь начальным и конечным положением заряда, работа определяется разностью потенциалов начальной и конечной точек.Для нахождения связи между напряженностью и потенциалом рассчитаем работу при бесконечно малом перемещении точечного заряда в электрическом поле из точки 0 в точку А Элементарная механическая работа при таком перемещении вычисляется так: 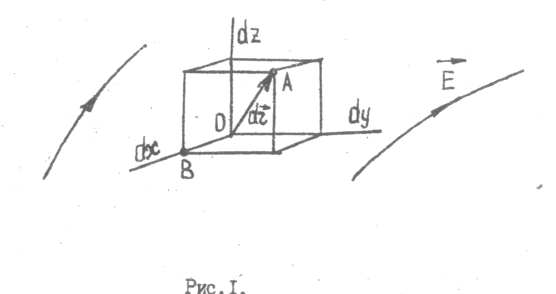  В соответствие с формулой (2) эта же работа равна: 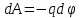 Так как напряжение между двумя точками поля численно равно работе сил поля по перемещению единичного заряда q между этими точками, можно отметить, что в однородном поле напряжение будет равно по модулю Δϕ U = - Δϕ = - (ϕ2 – ϕ1) = ϕ1 - ϕ2 Схема лабораторной установки. Неподвижные электроды ванны 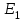 и и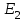 подключены к источнику постоянного напряжения G. подключены к источнику постоянного напряжения G.Подвижный электрод-зонд 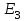 подключен к источнику тока через вольтметр V. При погружении зонда в электролит вольтметр показывает разность потенциалов между неподвижным левым по схеме электродом подключен к источнику тока через вольтметр V. При погружении зонда в электролит вольтметр показывает разность потенциалов между неподвижным левым по схеме электродом 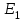 и подвижным зондом и подвижным зондом 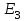 . .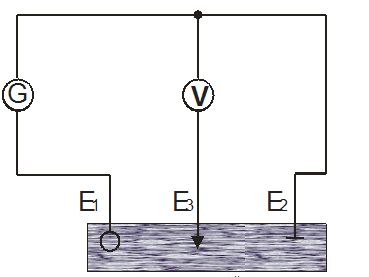 Силовые и эквипотенциальные линии. Доказательство их взаимной перпендикулярности в каждой точке поля. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Покажем, что в каждой точке пространства вектор напряжённости электрического поля 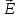 перпендикулярен эквипотенциальной поверхности и направлен в сторону уменьшения потенциала. Для этого рассчитаем работу по перемещению заряда перпендикулярен эквипотенциальной поверхности и направлен в сторону уменьшения потенциала. Для этого рассчитаем работу по перемещению заряда 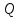 вдоль эквипотенциальной поверхности на бесконечно малое расстояние вдоль эквипотенциальной поверхности на бесконечно малое расстояние 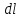 Такая работа равна нулю, поскольку определяется разностью потенциалов точек 1 и 2.  С другой стороны, работа записывается так: 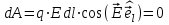 где 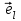 - единичный вектор, направленный по касательной к эквипотенциальной поверхности. - единичный вектор, направленный по касательной к эквипотенциальной поверхности.Косинус угла между векторами 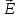 и и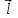 равен нулю, так как равен нулю, так как  где x1,x2 – координаты двух точек, лежащих на силовой линии; φ1, φ2 – потенциалы этих точек, вектор 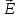 перпендикулярен эквипотенциальной поверхности. перпендикулярен эквипотенциальной поверхности. Далее переместимся по нормали  к эквипотенциальной поверхности в сторону уменьшения потенциала. В этом случае к эквипотенциальной поверхности в сторону уменьшения потенциала. В этом случае  и из формулы и из формулы 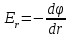 следует, что следует, что 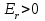 . Значит, вектор . Значит, вектор 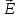 направлен по нормали в сторону уменьшения потенциала. направлен по нормали в сторону уменьшения потенциала.Ошибка! Нет определения силовых линий электрического поля. Что это такое, как и для чего их проводят? Силовая линия электрического поля – это геометрическая кривая, в каждой точке которой вектор напряжённости электрического поля направлен к ней по касательной  Число силовых линий, приходящихся на единичную перпендикулярную к ним площадь поверхности, характеризует абсолютную величину напряжённости поля: чем гуще расположены силовые линии, тем больше величина напряжённости поля. Начинаются на положительных зарядах, заканчиваются на отрицательных зарядах По силовым линиям можно дать характеристику электрического поля. |
