Матлаб. Матрицы. матлаб. Лабораторная работа 1 по дисциплине Математическое моделирование средств измерений студент гр.
 Скачать 183.99 Kb. Скачать 183.99 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ ОТЧЁТ ЗАЩИЩЁН С ОЦЕНКОЙ______ ПРЕПОДАВАТЕЛЬ
Лабораторная работа №1 по дисциплине: Математическое моделирование средств измерений
Санкт-Петербург 2022 Цель работы: изучить различные операции по работе с матрицами и уравнениями, провести вычисления с помощью встроенных функций MATLAB, исходя из полученного задания Ход работы Задание №1 Дано:  Рисунок 1 – Исходные данные 4 варианта для задания №1 Найти: A′, B′; С = 3 * А – 8 * В, А * В, В * А. Операции с матрицами провести по определению из линейной алгебры и при помощи операций MATLAB. Решение: MATLAB использует оператор апострофа ('), чтобы выполнять комплексное сопряженное транспонирование.   Рисунок 2 – Транспонированные матрицы A и B Для получения матрицы С используется умножение каждой матрицы с последующим вычитанием произведений. 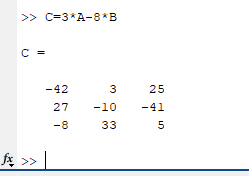 Рисунок 3 – Получение матрицы С MATLAB использует звездочку (*), чтобы обозначить умножение матриц. Умножение матриц не является коммутативным. То есть, A*B обычно не равно B*A, что соответствует вычислениями на рисунке 4.  Рисунок 4 – Умножение матриц Задание №2 Дано:  Рисунок 1 – Исходные данные 4 варианта для задания №2 Найти: А^-1 , В^-1 , А*А^-1 , А^-1 *А, В*В^-1 , В^-1*В. Вычисления произвести методом элементарных преобразований над расширенной матрицей и при помощи встроенных функций MATLAB. Решение: Получим обратную матрицу А  Детерминант отличен от нуля, а значит обратная матрица А существует.  Строим расширенную матрицу для дальнейших вычислений  Получаем единицы и нули на позициях  Полученная обратная матрица А. Теперь следует проверить полученный результат встроенной функцией MATLAB 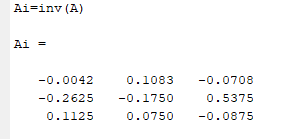 Получим обратную матрицу В  Детерминант отличен от нуля, а значит обратная матрица B существует  Строим расширенную матрицу для дальнейших вычислений 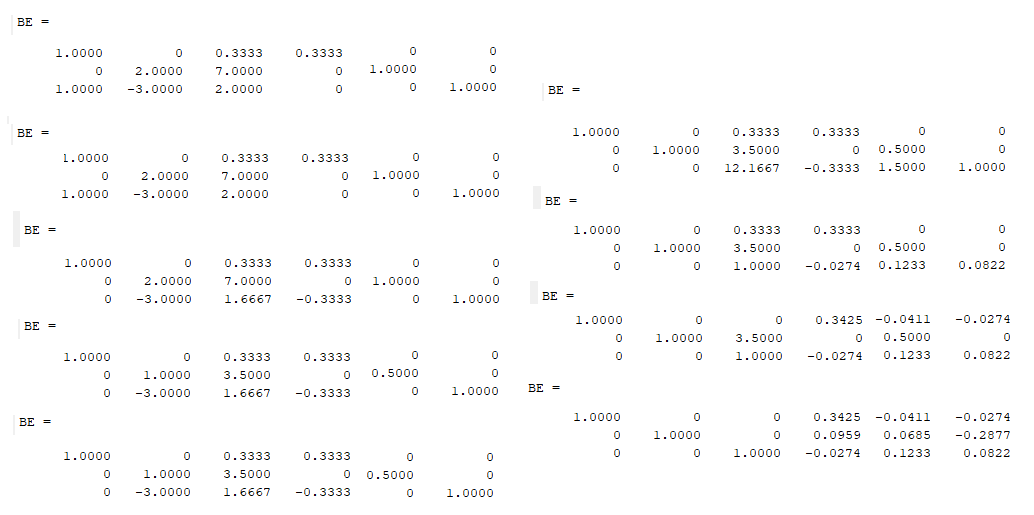 Получаем единицы и нули на позициях 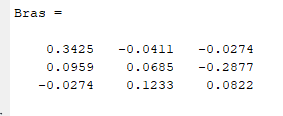 Полученная обратная матрица B. Теперь следует проверить полученный результат встроенной функцией MATLAB  Далее найдём произведения А*А^-1  Перемножив матрицу А на обратную матрицу А, получаем единичную матрицу. А^-1*А  Перемножив обратную матрицу А на матрицу А, получаем единичную матрицу. Вычисление двух данных произведений подтверждает верность обратной матрицы. В*В^-1 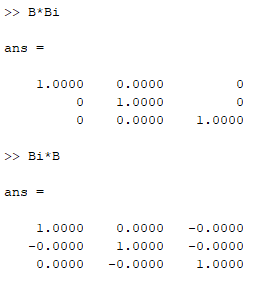 Перемножив матрицу B на обратную матрицу B, получаем единичную матрицу. В^-1*В  Перемножив обратную матрицу B на матрицу B, получаем единичную матрицу. Вычисление двух данных произведений подтверждает верность обратной матрицы. Задание №3 Дано: 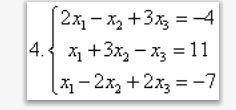 1 3 -1 1 3 -1Найти: решить системы линейных алгебраических уравнений методом Гаусса — Жордана и с помощью встроенных операций MATLAB. Решение: Запишем систему уравнений в виде матриц А и b 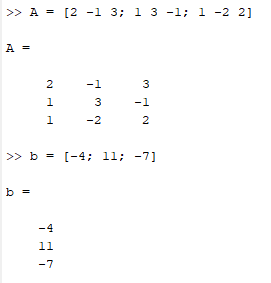 Для реализации этого метода требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю 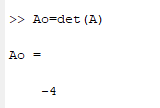 Решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов. Матрицы нужно перемножать именно так, что слева обратная матрица, справа матрица свободных членов. 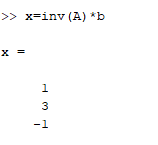 Проверка: подставляем найденные члены уравнений на места неизвестных  Вывод: В ходе работы были изучены основные операторы и функции MATLAB для работы с матрицами и системой уравнений. Использовались такие операции с матрицами как транспонирование, нахождение обратной матрицы, операции линейной алгебры. СЛАУ была решена методом Гаусса-Жордана. Также была произведена проверка найденных решений |
