Лабораторная работа Исследование прохождения сигналов через линейные цепи. СхемотехникаИУ_лаб1. Лабораторная работа 1 по дисциплине Схемотехника измерительных устройств исследование прохождения сигналов через линейные цепи

• Название: Лабораторная работа 1 по дисциплине Схемотехника измерительных устройств исследование прохождения сигналов через линейные цепи
• Анкор: Лабораторная работа Исследование прохождения сигналов через линейные цепи
• Дата: 28.11.2021
• Размер: 0.84 Mb.
• Имя файла: СхемотехникаИУ_лаб1.docx
• Тип: Лабораторная работа; #284441

Лабораторная работа № 1

по дисциплине: Схемотехника измерительных устройств

ИССЛЕДОВАНИЕ ПРОХОЖДЕНИЯ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ

Цель работы:исследование электрических процессов при прохождении сигналов различной формы через дифференцирующие и интегрирующие цепи.

Оборудование: универсальный лабораторный макет, осциллограф, генератор синусоидальных колебаний, генератор прямоугольных колебаний.

1. 
   Ход работы
   

1. 
   Собираем схему интегрирующей цепи, устанавливаем параметры элементов: R = 1 кОм, С = 1мкФ.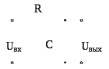
   

Рисунок 1 – Схема интегрирующей цепи

Подаем на схему сигнал напряжением 1 В и изменяем частоту от 50 Гц до 20 кГц.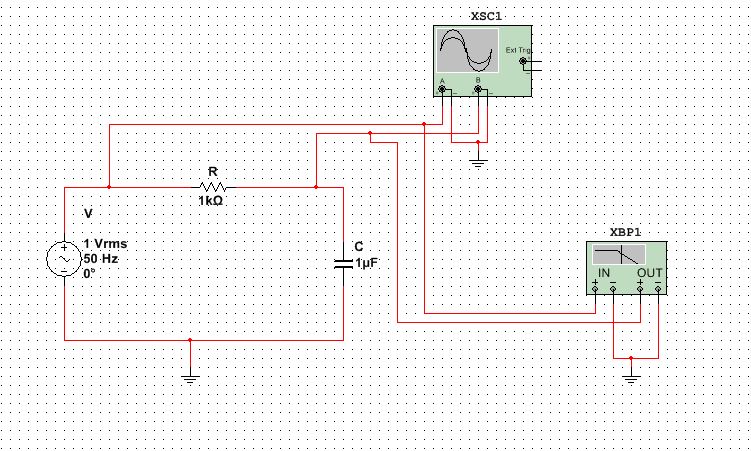



Рисунок 2 – Схема интегрирующей цепи в Multisim 12.0

2. 
   Снимаем АЧХ интегрирующей цепи.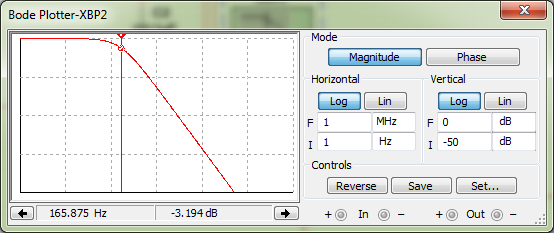
   

Рисунок 3 – АЧХ интегрирующей цепи

3. 
   Определяем коэффициент передачи цепи для нескольких значений (таблица 1).
   

Таблица 1 – Рассчитанные и измеренные значения

f, Гц	ω, рад/с	Uвхrms, В	Uвых.ам., В	Uвыхrms, В	K, дБ
50	314,16	1	1,414	1,000	-0,00131
100	628,32	1	1,174	0,830	-1,61694
150	942,48	1	1,022	0,723	-2,82128
160	1005,31	1	1,045	0,739	-2,62797
170	1068,14	1	1,032	0,730	-2,73671
200	1256,64	1	0,958	0,677	-3,38299
300	1884,96	1	0,814	0,576	-4,79781
400	2513,27	1	0,503	0,356	-8,97894
500	3141,59	1	0,43	0,304	-10,3409
600	3769,91	1	0,351	0,248	-12,1042
750	4712,39	1	0,295	0,209	-13,6139
900	5654,87	1	0,251	0,177	-15,0168
1050	6597,34	1	0,209	0,148	-16,6074
1200	7539,82	1	0,181	0,128	-17,8567
1500	9424,78	1	0,148	0,105	-19,6051
2500	15707,96	1	0,088	0,062	-24,1206
5000	31415,93	1	0,044	0,031	-30,1412
10000	62831,85	1	0,021	0,015	-36,5659
15000	94247,78	1	0,013	0,009	-40,7314
20000	125663,71	1	0,01	0,007	-43,0103
30000	188495,56	1	0,005	0,004	-49,0309
50000	314159,27	1	0,004	0,003	-50,9691
100000	628318,53	1	0,002	0,001	-56,9897
150000	942477,80	1	0,001	0,001	-63,0103
200000	1256637,06	1	0	0,000	0

4. 
   Строим график зависимости к = f(ω).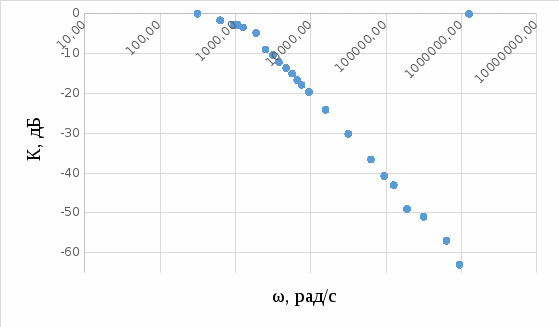
   

Рисунок 4 – График зависимости к = f(ω)

5. 
   Собираем схему дифференцирующей цепи.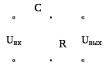
   

Рисунок 5 – Схема дифференцирующей цепи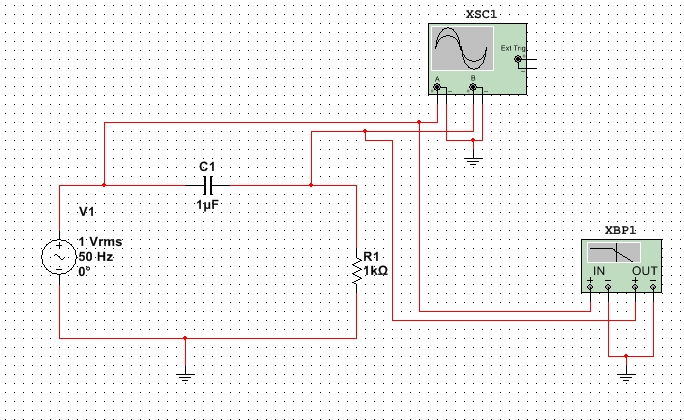



Рисунок 6 – Схема дифференцирующей цепи в Multisim 12.0

6. 
   Снимаем АЧХ дифференцирующей цепи.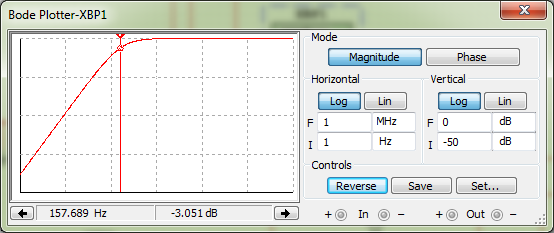
   

Рисунок 7 – АЧХ дифференцирующей цепи

7. 
   Определяем коэффициент передачи цепи для нескольких значений (таблица 2).
   

Таблица 2 – Рассчитанные и измеренные значения

f, Гц	ω, рад/с	Uвхrms, В	Uвых.ам., В	Uвыхrms, В	K, дБ
50	314,16	1	0,421	0,298	-10,5247
100	628,32	1	0,733	0,518	-5,70822
150	942,48	1	0,964	0,682	-3,32876
160	1005,31	1	1,004	0,710	-2,97563
170	1068,14	1	1,098	0,776	-2,19825
200	1256,64	1	1,11	0,785	-2,10384
300	1884,96	1	1,312	0,928	-0,65162
400	2513,27	1	1,393	0,985	-0,13128
500	3141,59	1	1,387	0,981	-0,16877
600	3769,91	1	1,402	0,991	-0,07534
750	4712,39	1	1,438	1,017	0,144878
900	5654,87	1	1,424	1,007	0,0599
1050	6597,34	1	1,394	0,986	-0,12504
1200	7539,82	1	1,425	1,008	0,065997
1500	9424,78	1	1,408	0,996	-0,03825
2500	15707,96	1	1,398	0,989	-0,10016
5000	31415,93	1	1,363	0,964	-0,32038
10000	62831,85	1	1,375	0,972	-0,24425
15000	94247,78	1	1,341	0,948	-0,46172
20000	125663,71	1	1,387	0,981	-0,16877
30000	188495,56	1	1,415	1,001	0,004829
50000	314159,27	1	1,429	1,010	0,090345
100000	628318,53	1	1,491	1,054	0,459253
150000	942477,80	1	1,35	0,955	-0,40362
200000	1256637,06	1	1,337	0,945	0

8. 
   Строим график зависимости к = f(ω).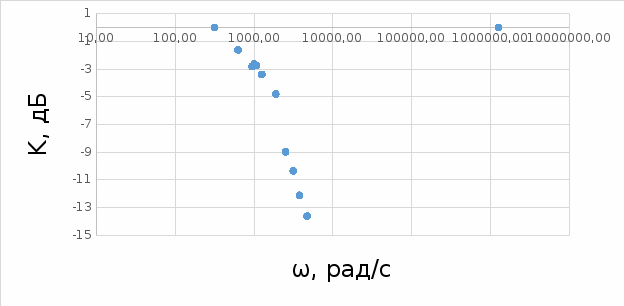
   

Рисунок 8 – График зависимости к = f(ω)

9. 
   Снимаем ФЧХ интегрирующей цепи.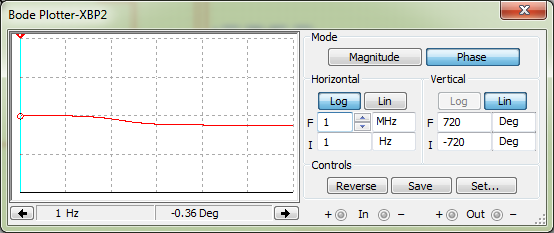
   

Рисунок 9 – ФЧХ интегрирующей цепи

10. 
    Снимаем ФЧХ дифференцирующей цепи.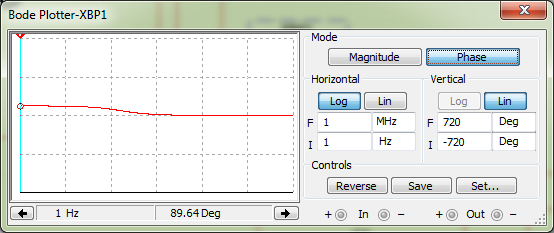
    

Рисунок 10 – ФЧХ дифференцирующей цепи

11. 
    По экспериментальным графикам определяем значения верхней (ω_в) и нижней (ω_н): ω_в = f_В*2*π = 165,875*2*π = 1042,22 рад/с, ω_н = f_Н*2*π = 157,689*2*π = 990,79 рад/с. Рассчитываем постоянные времени τ_экс = 1/ω и τ_расч = RC.
    

τ_экс =1/ω_в =1/165,875 = 0,006 мс;

τ_экс = 1/ω_н = 1/157,689 = 0,0063 мс;

τ_расч = RC =1*10³*1*10^-6 = 10^-3мс.

12. 
    Исследуем переходные характеристики интегрирующей цепи. Для этого на вход подаём с генератора прямоугольных колебаний импульсы амплитудой 1 В, периодом колебаний 6 мс, длительностью 3 мс. Зарисовываем форму выходных импульсов и по осциллограмме определяем постоянную времени цепи. τ = 1,515мс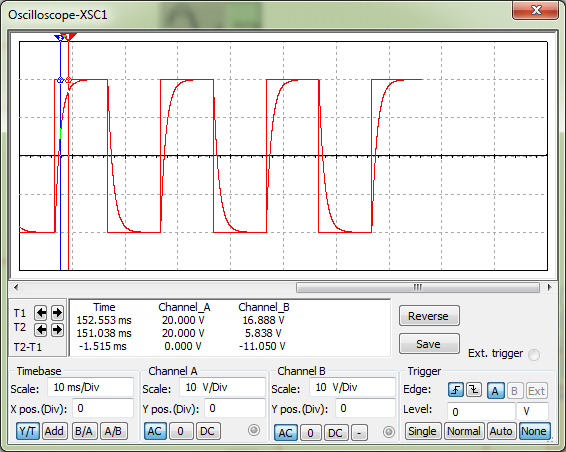
    

Рисунок 11 – Переходные характеристики интегрирующей цепи

13. 
    Исследуем переходные характеристики дифференцирующей цепи. Для этого на вход подаём с генератора прямоугольных колебаний импульсы амплитудой 1 В, периодом колебаний 6 мс, длительностью 3 мс. Зарисовываем форму выходных импульсов и по осциллограмме определяем постоянную времени цепи. τ = 1,326мс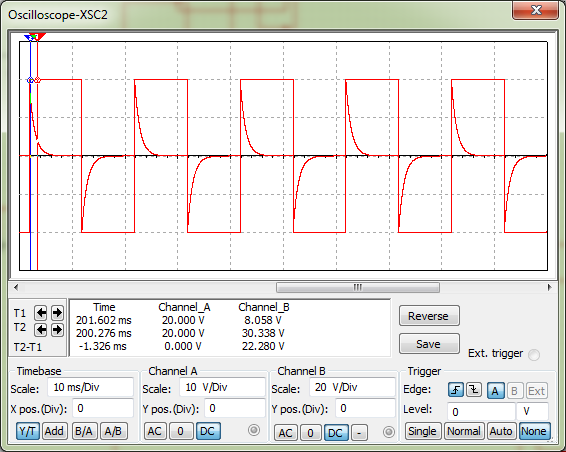
    

Рисунок 12 – Переходные характеристики дифференцирующей цепи

14. 
    Собираем схему ППФ.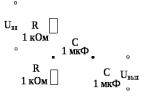
    

Рисунок 13 – Схема ППФ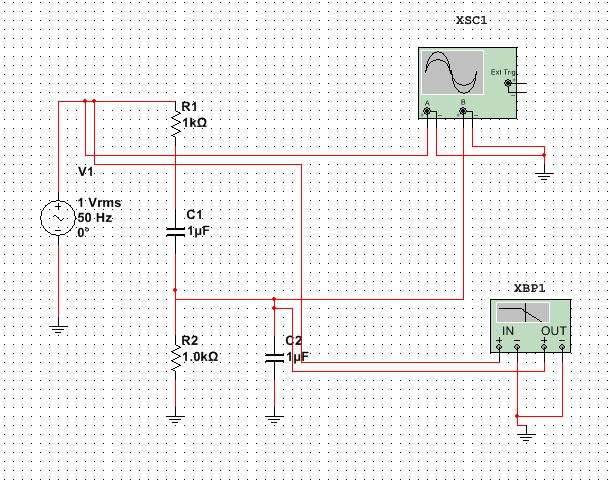



Рисунок 14 – Схема ППФ в Multisim 12.0

15. 
    Снимаем АЧХ ППФ.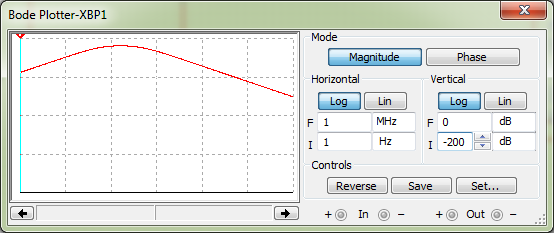
    

Рисунок 15 – АЧХ ППФ

16. 
    Снимаем ФЧХ ППФ.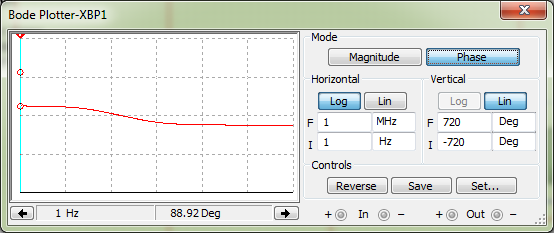
    

Рисунок 16 – ФЧХ ППФ

17. 
    Определяем коэффициент передачи цепи для нескольких значений (таблица 3).
    

Таблица 3 – Рассчитанные и измеренные значения

f, Гц	ω, рад/с	Uвхrms, В	Uвых.ам., В	Uвыхrms, В	K, дБ
50	314,16	1	0,345	0,244	-12,2539
100	628,32	1	0,441	0,312	-10,1215
150	942,48	1	0,459	0,325	-9,77405
160	1005,31	1	0,465	0,329	-9,66124
170	1068,14	1	0,48	0,339	-9,38548
200	1256,64	1	0,447	0,316	-10,0041
300	1884,96	1	0,391	0,276	-11,1668
400	2513,27	1	0,383	0,271	-11,3463
500	3141,59	1	0,331	0,234	-12,6137
600	3769,91	1	0,31	0,219	-13,1831
750	4712,39	1	0,261	0,185	-14,6775
900	5654,87	1	0,22	0,156	-16,1618
1050	6597,34	1	0,196	0,139	-17,1652
1200	7539,82	1	0,176	0,124	-18,1
1500	9424,78	1	0,139	0,098	-20,15
2500	15707,96	1	0,087	0,062	-24,2199
5000	31415,93	1	0,043	0,030	-30,3409
10000	62831,85	1	0,022	0,016	-36,1618
15000	94247,78	1	0,015	0,011	-39,4885
20000	125663,71	1	0,01	0,007	-43,0103
30000	188495,56	1	0,006	0,004	-47,4473
50000	314159,27	1	0,004	0,003	-50,9691
100000	628318,53	1	0,002	0,001	-56,9897
150000	942477,80	1	0,0017	0,001	-58,4013
200000	1256637,06	1	0,0014	0,001	0

18. 
    Подаём на вход ППФ прямоугольные импульсы. Зарисовываем временные диаграммы работы цепи для трёх периодов: Т1 = 100; Т2 = 1000; Т3 = 100000.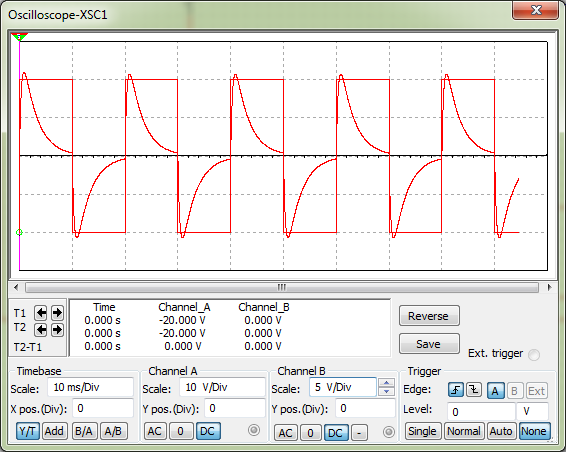
    

Рисунок 17 – Временная диаграмма работы цепи ППФ

19. 
    Собираем схему ПЗФ (рисунок 20).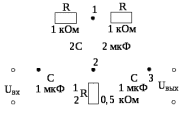
    

Рисунок 18 – Схема ПЗФ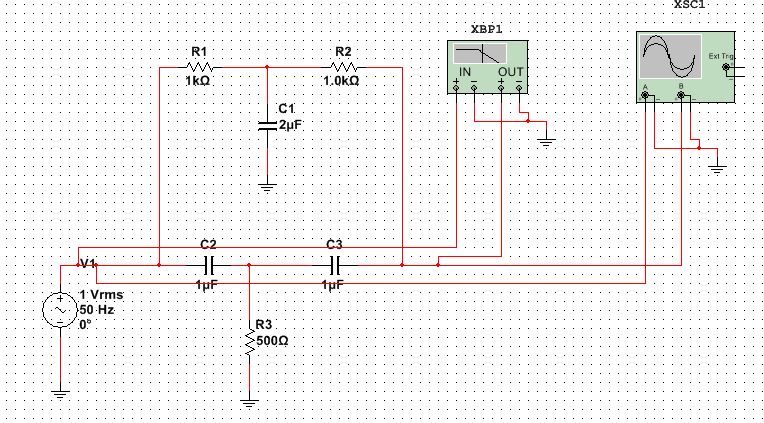



Рисунок 19 – Схема ПЗФ в Multisim 12.0

20. 
    Снимаем АЧХ ПЗФ (рисунок 20).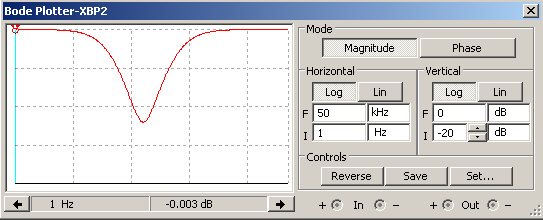
    

Рисунок 20 – АЧХ ПЗФ

21. 
    Снимаем ФЧХ ПЗФ (рисунок 21).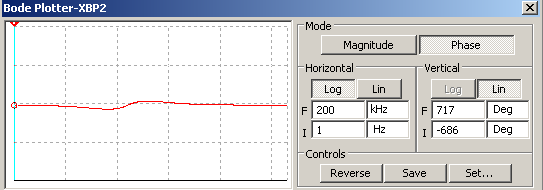
    

Рисунок 21 – ФЧХ ПЗФ

22. 
    Определяем коэффициент передачи цепи для нескольких значений (таблица 4).
    

Таблица 4 – Рассчитанные и измеренные значения

f, Гц	ω, рад/с	Uвхrms, В	Uвых.ам., В	Uвыхrms, В	K, дБ
50	314,16	1	0,821	0,581	-4,72344
100	628,32	1	0,359	0,254	-11,9084
150	942,48	1	0,043	0,030	-30,3409
160	1005,31	1	0,004	0,003	-50,9691
170	1068,14	1	0,048	0,034	-29,3855
200	1256,64	1	0,162	0,115	-18,82
300	1884,96	1	0,459	0,325	-9,77405
400	2513,27	1	0,643	0,455	-6,84608
500	3141,59	1	0,809	0,572	-4,85133
600	3769,91	1	0,987	0,698	-3,12396
750	4712,39	1	1,036	0,733	-2,7031
900	5654,87	1	1,132	0,800	-1,93337
1050	6597,34	1	1,171	0,828	-1,63916
1200	7539,82	1	1,238	0,875	-1,15589
1500	9424,78	1	1,268	0,897	-0,94791
2500	15707,96	1	1,385	0,979	-0,1813
5000	31415,93	1	1,384	0,979	-0,18758
10000	62831,85	1	1,382	0,977	-0,20014
15000	94247,78	1	1,371	0,969	-0,26955
20000	125663,71	1	1,399	0,989	-0,09395
30000	188495,56	1	1,389	0,982	-0,15626
50000	314159,27	1	1,4	0,990	-0,08774
100000	628318,53	1	1,399	0,989	-0,09395
150000	942477,80	1	1,385	0,979	-0,1813
200000	1256637,06	1	1,406	0,994	0

23. 
    Подаём на вход ПЗФ прямоугольные импульсы. Зарисовываем временные диаграммы работы цепи для трёх периодов: Т1 = 1000; Т2 = 100; Т3 = 100000.