задачи по метрологии. Задача 1. Решение. Для записи результатов формируем таблицу (табл. 1), в столбцы которой будем записывать измеренные значения

• Название: Решение. Для записи результатов формируем таблицу (табл. 1), в столбцы которой будем записывать измеренные значения
• Анкор: задачи по метрологии
• Дата: 30.05.2022
• Размер: 135.5 Kb.
• Имя файла: Задача 1.doc
• Тип: Задача; #558168

Задача 1

Вольтметром со шкалой (0…50) В, имеющим приведенную погрешность γV = 2%, измерены значения напряжения 0; 5; 10; 20; 40; 50 В.

Рассчитать зависимости абсолютной, относительной и приведённой по-

грешностей от результата измерений. Результаты представить в виде таб-

лицы и графиков.

Решение.

Для записи результатов формируем таблицу (табл. 1.1), в столбцы которой будем записывать измеренные значения V, абсолютные V, относительные V и приведённые V погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 5; 10; 20; 40; 50 В.

Значение абсолютной погрешности известно из условий задачи

( ) и считается одинаковым для всех измеренных значений напряжения; это значение заносим во все ячейки второго столбца.

Значения относительной погрешности будем рассчитывать по формуле

.

При V=0 В получаем .

При V=5 В получаем .

При V=10 В получаем .

При V=20 В получаем .

При V=40 В получаем .

При V=50 В получаем .

Полученные таким образом значения относительной погрешности

заносим в третий столбец.
Для расчёта значений приведённой погрешности будем использовать

формулу:

.

Предварительно определим нормирующее значение .

Так как диапазон измерений вольтметра – (0…50) В, то шкала

вольтметра содержит нулевую отметку, следовательно, за нормирующее

значение принимаем размах шкалы прибора, т.е.

.

Так как величины и постоянны при любых измеренных значениях напряжения, то величина приведённой погрешности так же постоянна и составляет . Это значение заносим во все ячейки четвёртого столбца.

По данным табл. 1.1 строим графики зависимостей абсолютной ,

относительной и приведённой погрешностей от результата измерений V (рис. 1.1).

В данном случае графики зависимостей абсолютной и приведённой

погрешностей сливаются друг с другом и представляют собой горизонтальные прямые линии. График зависимости относительной погрешности представляет собой гиперболу.

Таблица 1 - Результаты расчёта значений погрешностей

V, В	∆V, B	δV,%	γV,%
1	2	3	4
0	1	∞	2
5	1	20	2
10	1	10	2
20	1	5	2
40	1	2,5	2
50	1	2	2

Так же представим результаты измерений и расчетов в виде графиков зависимостей абсолютной,относительной и приведенной погрешностей от результата имерений (рисунок 1)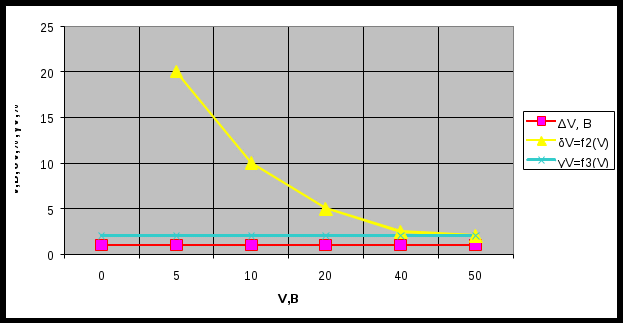



Рисунок 1 - Графики зависимостей абсолютной, относительной

и приведённой погрешностей от результата измерений
Задача 2

Амперметром класса точности 0.1 со шкалой (0…5) А

измерены значения тока 0;0,5;1,0;1,5;2,0;3,0;4,0;5,0 А. Рассчитать зависимости абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

Решение.

Для записи результатов формируем таблицу (табл. 2.1), в столбцы

которой будем записывать измеренные значения I, абсолютные ΔI, относительные δI и приведённые ɤI погрешности.

В первый столбец записываем заданные в условии задачи измеренные

значения тока: 0; 0,5;1,0;1,5;2,0;3,0;4,0;5,0 А.

Класс точности амперметра задан числом без кружка, следовательно,

приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. | ɤI | ≤ 0,1%.

При решении задачи рассмотрим худший случай | ɤI | = 0,1%, когда

приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует ɤI = +0,1% и ɤI = –0,1 %.

Рассчитаем значения абсолютной погрешности.

Из формулы ɤI = (ΔI/I_n)×100 % выражаем абсолютную погрешность

ΔI=( ΔI× I_n)/100 %.За нормирующее значение I_n принимаем размах шкалы, так как шкала амперметра содержит нулевую отметку, т.е.

I_n = |5,0 А – 0 А| = 5,0 А

Тогда абсолютная погрешность равна ΔI=(±0,1 % ×5,0 А)/100% =±0,5А

во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.

Значения относительной погрешности будем рассчитывать по формуле

δI = (ΔI/ I)×100 %

При I = 0 А получаем δI=(±0,5 А/0 А)×100 % → ∞

При I = 0.5 А получаем δI=(±0,5 А/0.5 А)×100 % =±100 %

При I = 1.0 А получаем δI=(±0,5 А/1.0 А)×100 % =±50 %

При I = 1.5 А получаем δI=(±0,5 А/1.5 А)×100 % =±33 %

При I = 2.0 А получаем δI=(±0,5 А/2.0 А)×100 % =±25 %

При I = 3.0 А получаем δI=(±0,5 А/3.0 А)×100 % =±17 %

При I = 4.0 А получаем δI=(±0,5 А/4.0 А)×100 % =±12,5 %

При I = 5.0 А получаем δI=(±0,5 А/5.0 А)×100 % =±10 %

Для записи результатов сформируем таблицу (табл.2)

Таблица 2 - результат расчета значений погрешностей

I ,А	ΔI, А	δI, %	ɤI ,%
1	2	3	4
0	±0,5	±∞	±0,5
0.5	±0,5	±100	±0,5
1.0	±0,5	±50	±0,5
1.5	±0,5	±33	±0,5
2.0	±0,5	±25	±0,5

Таблица 2 - результат расчета значений погрешностей

3.0	±0,5	±17	±0,5
4.0	±0,5	±12,5	±0,5
5.0	±0,5	±10	±0,5

По данным табл. 2, учитывая, что погрешности могут быть как

положительными, так и отрицательными, строим графики зависимостей абсолютной ΔI, относительной δI и приведённой ɤI погрешностей от результата измерений I (рисунок 2).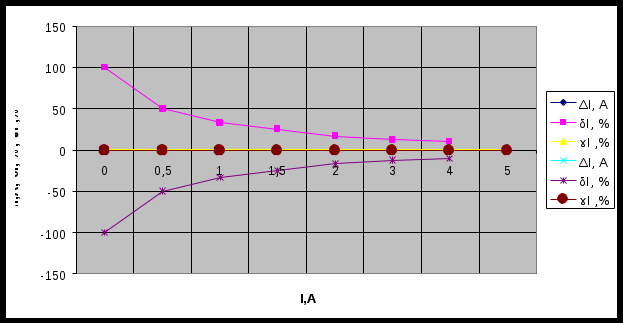



Рисунок 2 - Графики зависимостей абсолютной, относительной и приведённой погрешностей от результата измерений
Задача 3

При многократном измерении физической величины I получен ряд измеренных значений в IА : 85,6;85,7;85,9;85,6;85,7;85,8;84,12;85,6;85,9;85,9; 85,7;85,8;85,7;85,8;85,9;85,6. Используя критерий Романовского необходимо проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р = 0,99.

Решение.

Определим среднее арифметическое значение Мх

М_х=(85,6+85,7+85,9+85,6+85,7+85,8+84,12+85,6+85,9+85,9+85,7+85,8+85,7+ 85,8+85,9+85,6)/16=1370,32/16=85,65 %

Рассчитаем среднее квадратическое отклонение S_x данного ряда

S_x = (0,05²+(-0,05)²+0,25²+0,05²+(-0,05²)+(-0,15)²+1,53²+0,05²+ (-0,25)²+ (-0,25)²+ +(-0,05)²+(-0,15²)+ (-0,05)² +(-0,15²)+(-0,25)² +0,05²/16-1)=0,18.

Из ряда измеренных значений напряжения выбираем результаты, подозрительные на содержание грубой погрешности: наименьший х_min =84,12 А и наибольший х_max = 85,9 А

Рассчитываем критерий β_min для х_min = 84,12 А

β_min =(|85,65-84,12|)/0,18=8,5.

Рассчитываем критерий β_max для х_max = 85,9 А

β_max =(|85,65-85,9|)/0,18=1,4.

При заданном значении доверительной вероятности Р=0,99 и числа измерений n=16 находим теоретический уровень значимости β_т для данного ряда β_т = 2,965

Значение β_т для n = 16 находится следующим образом

β_т/n=16 =(( β_т/n=15)+( β_т/n=17))/2

Сравним значения β_min и β_max с найденным значением β_т:

8,5 >2,965, т.е. β_min > β_т,

следовательно результат х_min = 84,12 А не содержит грубую погрешность и его следует исключить из ряда измеренных значений.

1,4< 2,965, т.е. β_max < β_т,

следовательно результат х_max = 85,9 А содержит грубую погрешность и его следует оставить в ряду измеренных значений.

После исключения промаха из ряда значений необходимо пересчитать значения М_х, S_x, β_min и β_max, так как изменилось х_min (х_min = 85,6 А) и количество измерений n (n = 15).

М_х = 85,75; S_x = 0,02; β_min = 7,5 для х_min = 85,6 В; β_max = 7,5 для х_max = 85,9 А; β_т/n=14 = 7,5.

Как видно 7,5> 2,946 т.е. β_min > βт, и 7,5> 2,946, т.е. β_max > β_т

Из приведённых расчётов следует, что полученный ряд измеренных значений силы электрического тока содержит промахи с вероятностью Р = 0,99.
Задача 4

При многократном измерении длины балки L получены значения в мм: 90,3; 90; 89,8; 89,9; 90,4; 90; 90,3; 89,1; 90,5; 90,4; 90. Укажите доверительные границы истинного значения длины с вероятностью Р = 0,95.

Решение.

Находим среднее значение L

L=(90,3+90+89,8+89,9+90,4+90+90,3+89,1+90,5+90,4+90)/11=90,06мм. Вычислим по формуле среднее квадратическое отклонение среднего

арифметического S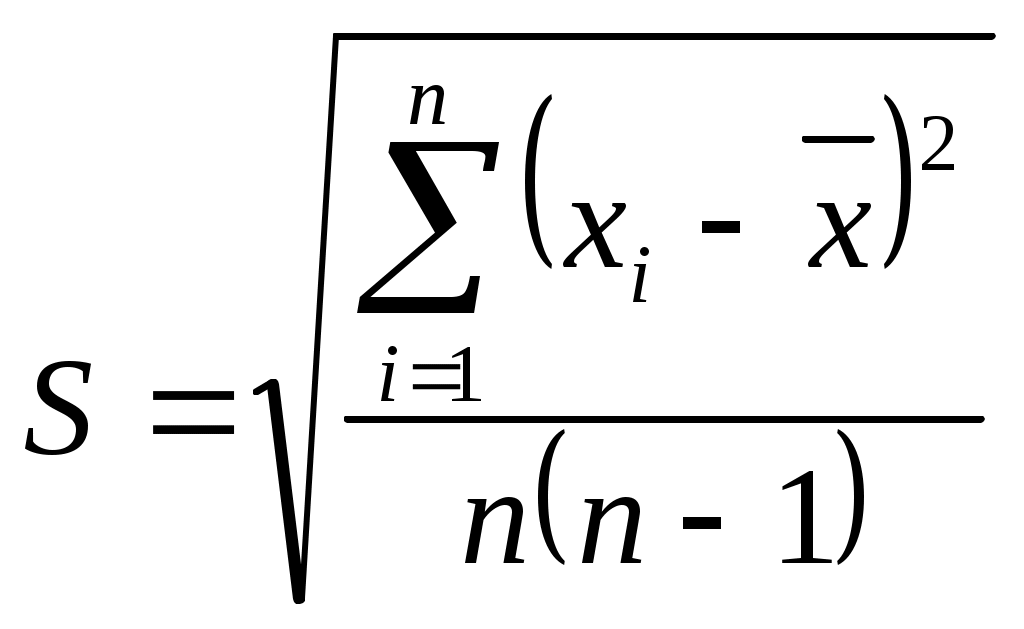



Тогда получим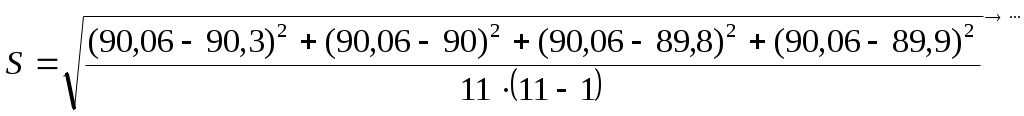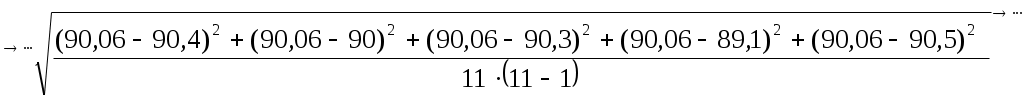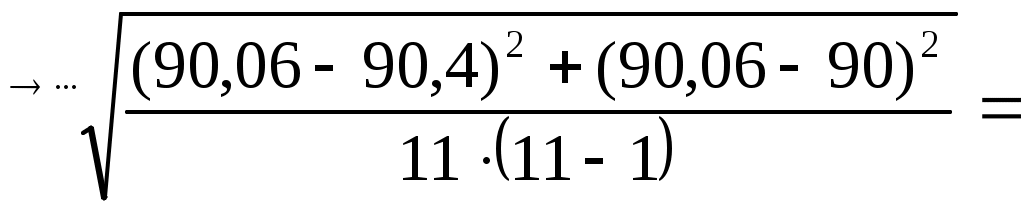





0,12

По таблице находим значение L_n,Pпри доверительной вероятности Р = 0,95 и n – 1 = 10

L_n,P=2,228

Доверительные границы истинного значения длины балки с вероятностью Р = 0,95 рассчитываются по формуле:

90,1-0,12×2,228˂ L ˂90,1+0,12×2,228

Окончательный результат измерения длины L балки

89,83 ˂ L ˂90,37 ; Р = 0,95 или L = 90,1 ± 0,27 мм; Р = 0,95.

Задача 5

Расчётная зависимость косвенного метода измерений имеет вид y=(b-a)(c+d)/[3e²]. Найти предельные и среднеквадратические оценки абсолютной и относительной погрешности косвенного измерения величины y. Δ a = 1; Δ b = 3;Δ c = 2; Δ d = 2; Δ e = 1; a=50; b= 90; c= 60; d =70; e= 40

Решение.

Введем обозначение А = (b-a), В=(c+d) тогда y = AВ/[3e²].

Прологарифмируем левую и правую часть заданной зависимости:

ln y = lnА + ln B – ln 3 – 2 ln e

Найдем дифференциал правой и левой частей:

d ln y=d ln A + d ln B – d ln3 – 2 d ln e

С учётом того, что получим ln 3 =0 , тогда

d ln y= d ln A + d ln B – 2 d ln e

Учитывая, что дифференциал от логарифма переменной величины

находится по формуле d (ln x) = ((d ln x)/d x)×d x = d x / x, получаем:

d y = (d A /A) + (d B/ B) – (2 d e/ e)

Произведем широко используемую в теории погрешностей замену

дифференциалов малыми абсолютными погрешностями(при условии, что абсолютные погрешности достаточно малы);

dy ≈ Δy; d A ≈ Δ A ; d B ≈ Δ B; de ≈ Δe; тогда

Δy/y = ΔA/A – ΔB/B – 2Δ e/e

Учитывая, что знаки погрешностей ΔA ; ΔB; Δe заранее неизвестны, для получения гарантированной (предельной) оценки относительной погрешности косвенного измерения в последней формуле все знаки «-» заменяем на знаки «+»

(Δy/y)_пр =Δ A / A + Δ B/ B + 2 Δ e/e

Вводим обратную замену А = b – a, B = c + d

(Δ y/y) _пр = ((Δb –Δa) / b-a) + (Δc+ Δd /с +d )+2 Δe/e )
Предельную оценку абсолютной погрешности косвенного измерения

находим по формуле

Δy_пр = δ y_пр y

Δy _пр =((Δb–Δa) / (b–a) + (Δc + Δd) / (c + d) /2 Δe/e))× ((b-a) (c + d))/[3e²]

Найдём среднеквадратические оценки относительной и абсолютной

погрешностей косвенного измерения: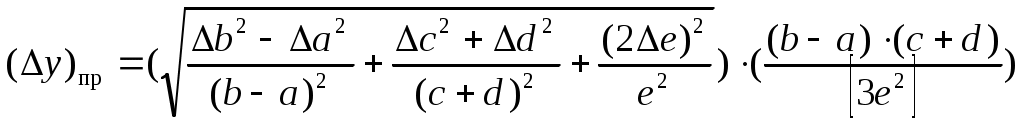





Вычисляем: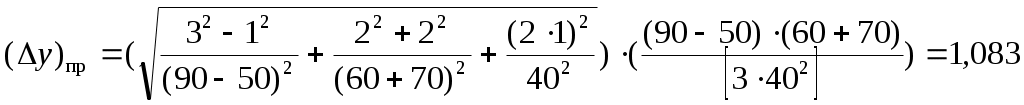


.