Знакомство со средой EXCEL. Статистическая обработка опытных данных.. Знакомство со средой EXCEL; Статистическая обработка опытных дан. Лабораторная работа 1 по дисциплине статическая радиотехника Знакомство со средой excel. Статистическая обработка опытных данных

• Название: Лабораторная работа 1 по дисциплине статическая радиотехника Знакомство со средой excel. Статистическая обработка опытных данных
• Анкор: Знакомство со средой EXCEL. Статистическая обработка опытных данных
• Дата: 21.06.2021
• Размер: 57.44 Kb.
• Имя файла: Знакомство со средой EXCEL; Статистическая обработка опытных дан.docx
• Тип: Лабораторная работа; #219518

Лабораторная работа №1

по дисциплине

«СТАТИЧЕСКАЯ РАДИОТЕХНИКА»

Знакомство со средой EXCEL.

Статистическая обработка опытных данных.

Вариант №2

Цель: приобретение опыта статистической обработки опытных данных.

Необходимая среда: Microsoft EXCEL.

Задание 1. Имеется заданный таблицей закон распределения случайной величины. Требуется, используя встроенные функции EXCEL, найти среднее значение, дисперсию, среднее квадратическое отклонение и асимметрию случайной величины.

Формулы для нахождения искомых величин:

Математическое ожидание (ср.знач.) : Дисперсия: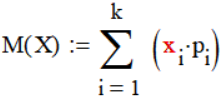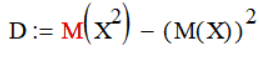

Среднее квадратическое отклонение :



Центральный момент СВ Х порядка 3 :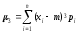



Асимметрия случайной величины :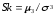



Таблица 1. Данные. Таблица 2. Расчет.

x(i) p(i) 0 0,216 1 0,432 2 0,288 3 0,064 сумма p(i)	1
мат.ожид.:	1,2
дисп.:	0,72
СКО:	0,848528
центр.мом3	0,144
асимметория	0,235702

Диаграмма 1. Распределение СВ Х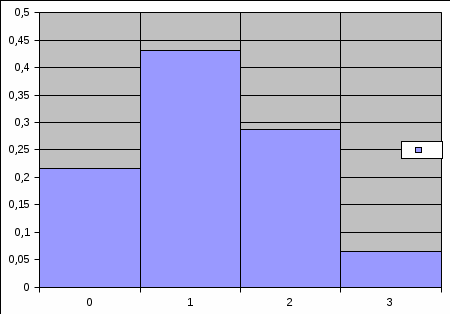




Задание2. Случайные величины Х и У представлены соответствующими выборками, состоящими из 100 значений. Построить гистограммы распределения этих величин. Используя критерий согласия хи-квадрат при уровне значимости 0.1 проверить гипотезу о распределении случайной величины Х по равномерному закону, а случайной величины У по нормальному закону.

Для построения гистограмм необходимо весь диапазон значений случайной величины разбить на интервалы и подсчитать количество значений, попавших в каждый интервал.

Для случайной величины Х рекомендуемая длина интервала 0.1, для У — 0.5. Учитывая, что значения Х лежат в диапазоне от 0 до 1, а значения У в диапазоне от -3.0 до 2.5 (для вычислений со значениям У используется выборка, 99 из 100 значений, одно из них отбрасывается с целью следования рекомендациям).

Для удобства вычислений найдем относительную частоту p_i^*=n_i/n, где n_i — количество значений в i-ом интервале, n — объем выборки.

Проверка гипотезы о законе распределения СВ производится с помощью критерия Пирсона (критерий хи-квадрат). Сначала определяется мера расхождения ² по формуле: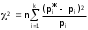

,

где k — количество интервалов (k=10),

n — объем выборки (100 значений – для X и 99 значений – для Y),

p_i — теоретическая вероятность попадания значения СВ в i-ый интервал при

предполагаемом законе распределения СВ.

Затем определяется табличное значение ²_,r при уровне значимости =0.1 с r степенями свободы (r = k-1) для значений X , а для значений Y уровень значимости =0.5 . Гипотеза считается правдоподобной, если ² <²_{,r, .} ²_,rнаходится с помощью встроенной функции.

В случае гипотезы о равномерном законе распределения СВ Х будем иметь: p_i=const=1/k=0.1. Рассчитаем: ²_0.1,9= 14.684, ²= 8.

Вывод: Полученные значения удовлетворяют условию² <²_,r , следовательно, гипотеза о распределении случайной величины Х по равномерному закону верна.

В случае гипотезы о нормальном законе распределения СВ У следует вычислить вероятности p_i для каждого интервала. Вероятности p_i вычисляются как разность значений функции распределения на краях соответствующего интервала, для нахождения значений этой функции необходимо еще вычислить среднее значение и стандартное отклонение. По приведенной выше формуле получаем ² =3,45.

Вывод:Полученное значение удовлетворяет условию² <²_,r , следовательно, гипотеза о распределении случайной величины У по нормальному закону верна.

Далее в таблицах приведены все значения, данные и вычисленные:

Таблица 3. Распределение СВ Х.

X	x(i)	n(i)	p(i)
0,289316	0,1	9	0,09
0,537426	0,2	10	0,1
0,514435	0,3	13	0,13
0,103434	0,4	6	0,06
0,414028	0,5	10	0,1
0,576717	0,6	6	0,06
0,876566	0,7	14	0,14
0,440039	0,8	13	0,13
0,729748	0,9	12	0,12
0,869264	1	7	0,07
0,715642
0,80072
0,706535
0,741716
0,019092
0,886031
0,524987
0,463323
0,065194		X^2 =	8
0,713422		альфа =	0,1
0,488943		r =	9
…		(X_0.1,9)^2 =	14,68366

Таблица 4. Распределение СВ У.

Y	y(i)	n(i)	p(i)	p`(i)	((p(i)-p`(i))^2)/p`(i)
-0,12744	-2	3	0,03030303	0,019559511	0,005901129
0,554172	-1,5	3	0,03030303	0,047192607	0,006044544
-1,09734	-1	13	0,131313131	0,091616786	0,017199903
-0,7313	-0,5	13	0,131313131	0,14311536	0,000973289
1,404732	0	16	0,161616162	0,17989731	0,001857729
-0,62021	0,5	19	0,191919192	0,181969755	0,000543999
0,237149	1	14	0,141414141	0,148118845	0,000303493
-1,58685	1,5	10	0,101010101	0,097017479	0,000164311
-0,40149	2	6	0,060606061	0,051133078	0,001754977
-0,77069	2,5	2	0,02020202	0,02168413	0,000101302
-0,26268
0,97649			Объем выборки n=100
0,977815	альфа =	0,1	среднее зн. Y =	0,02635875
1,170021	r =	9	станд.откл. s =	1,062799709
…	(X_0.5,10)^2 =	14,68365662	X^2 =	3,449622876

Графическое представление распределения СВ: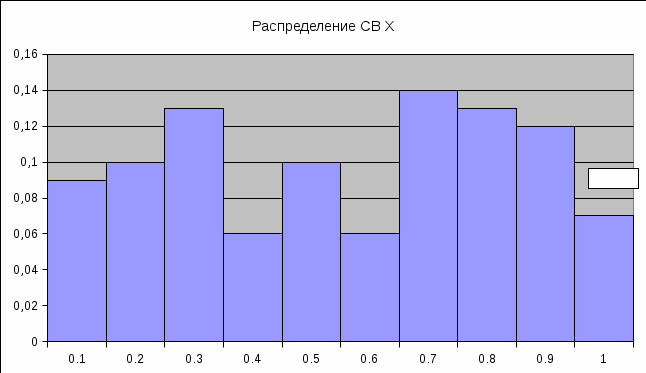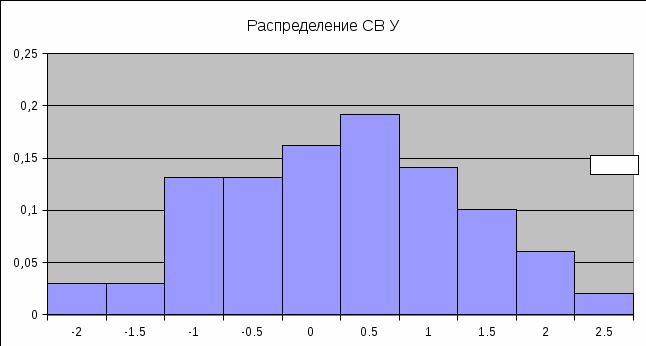