ЛАБОРАТОРНАЯ РАБОТА-1-испр. Лабораторная работа 1 по предмету Алгоритмические и аппаратные средства обработки информации

Название	Лабораторная работа 1 по предмету Алгоритмические и аппаратные средства обработки информации
Дата	02.03.2022
Размер	109.6 Kb.
Формат файла
Имя файла	ЛАБОРАТОРНАЯ РАБОТА-1-испр.docx
Тип	Лабораторная работа #379567

Министерство науки и высшего образования Российской Федерации

Ульяновский государственный технический университет

Лабораторная работа № 1 по предмету

«Алгоритмические и аппаратные средства обработки информации»

ВЫЧИСЛЕНИЕ РЕАКЦИИ ЛИНЕЙНОЙ ДИСКРЕТНОЙ СИСТЕМЫ

(Название лабораторной работы)

Учебная группа ИСТМД-11

	ФИО	Дата	Подпись
Студент	Шаблыгин В.В.
Преподаватель	Сазонов С.Н.

Ульяновск, 2022

ЦЕЛЬ РАБОТЫ:

изучение реакции ЛДС на входной сигнал.

Задача: Изучить метод расчета отклика линейной системы на произвольное воздействие с использованием формулы свертки.

Программа лабораторной работы

Ознакомиться с вышеуказанным методом.
Составить программу в соответствии с формулой.
Получить результаты и сделать выводы.

ОБОРУДОВАНИЕ И ПРИНАДЛЕЖНОСТИ:

Среда программирования SCILAB или PYTHON.

КРАТКАЯ ТЕОРИЯ:
Системой обработки сигналов (системой) называют объект, выполняющий требуемое преобразование (обработку) входного сигнала в выходной. Системой может быть, как физическое устройство, так и математическое преобразование.

Входной сигнал называют воздействием, выходной – реакцией (рис.№1).

Рис.№1. Линейная дискретная система.
Систему называют линейной, если она обладает свойствами:

аддитивности: реакция на сумму воздействий равна сумме реакций на каждое из воздействий (принцип суперпозиции). Другими словами, сумма входных сигналов порождает адекватную сумму выходных сигналов системы. Например, когда с одним абонентом разговаривают одновременно два, по параллельным телефонным аппаратам;
однородности (гомогенности, равномерности): умножению воздействия на весовой коэффициент соответствует реакция, умноженная на тот же коэффициент. Т.е. изменение амплитуды входного сигнала вызывает соответствующие изменения амплитуды выходного сигнала;

Соотношение вход/выход линейной системы описывается линейным уравнением.

Если система не обладает хотя бы одним из вышеперечисленных свойств, то она не может считаться линейной.

Инвариантность (нечувствительность к сдвигу во времени) - третье свойство, не является строго обязательным, но является основополагающим для большинства алгоритмов цифровой обработки сигналов. В системе, обладающей этим свойством, задержка воздействия на некоторое время приводит к задержке реакции на то же время. Такие системы называют стационарными.
Линейная система называется дискретной, если воздействие и реакция представляют собой дискретные сигналы x(nT) и y(nT).

Начальные условия дискретной системы могут быть нулевымиилиненулевыми. Признаком нулевыхначальных условий является отсутствие реакции y(nT) = 0, при отсутствии воздействия x(nT) = 0.

Дискретная система называется физически реализуемой, если для нее выполняются следующие условия (условия физической реализуемости):

при нулевых начальных условиях реакция не может возникнуть раньше воздействия;
значения реакции y(nT). в каждый момент времени n зависят от текущего x(nT) и предшествующих значений воздействия x[(n-m)T], m > 0 , но не зависят от его последующих значений x[(n-m)T], m > 0.

Характеристики ЛДС.

Во временной области основной характеристикой ЛДС является импульсная характеристика.

Импульсной характеристикой (ИХ) h(nT) ЛДСназывается ее реакция на цифровой единичный импульс u0(nT), при нулевых начальных условиях.

Во временной области соотношение вход/выход может описываться одним из двух разновидностей линейных уравнений:

формулой свертки (название уравнения), если для определения реакции используется импульсная характеристика;
разностным уравнением, если для определения реакции используются параметры ЛДС.

Любая линейная система осуществляет свёртку входного сигнала со своей

импульсной характеристикой.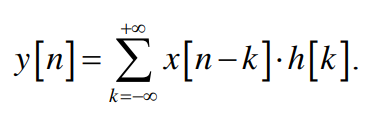

(1)

Формула свертки (1) непосредственно описывает алгоритм вычисления реакции по известному воздействию и импульсной характеристике ЛДС.

ВЫПОЛНЕНИЕ РАБОТЫ
Вариант № 8

Исходные данные:

	Значения отсчетов
	0	1	2	3	4	5	6	7	8	9
h(n)	2	2	3	3	3	4	4	2	1	0
x(n)	3	1	2	1	4	3	1	5	0	2

Где:

h(n) - импульсная характеристика системы;

x(n) - дискретный сигнал (воздействие).

Вычислим реакцию системы используя формулу свертки:

Текст программы:
"""
Задание: Для своего варианта вычислить реакцию ЛДС в виде 20 отсчетов при нулевых начальных условиях в
режиме калькулятора и с использованием программы. Построить графики импульсной характеристики, воздействия и реакции.
h(n) - Импульсная характеристика
x(n) - дискретный сигнал (воздействие)
y(n) - реакция
n - количество отсчетов
"""
import matplotlib.pyplot as plt
import pandas as pd

# Исходные данные:
h_n = [2, 2, 3, 3, 3, 4, 4, 2, 1, 0]
x_n = [3, 1, 2, 1, 4, 3, 1, 5, 0, 2]
n = 20

y_n = [] # реакция системы (искомое)

# если длина h(n) и x(n) меньше n, до дополним нулями:
if len(h_n) < n:
for i in range(n - len(h_n)):
h_n.append(0)
x_n.append(0)

# находим y(n):
for i in range(n):
for j in range(i + 1):
ls1 = h_n[:j + 1]
ls2 = x_n[:j + 1]
ls2.reverse()
y = 0
for h, x in zip(ls1, ls2):
y += h * x
y_n.append(y)

print('Реакция системы: ')
print(y_n)

# Построение графиков:
data = {'импульсная характеристика h(n)': h_n}
df = pd.DataFrame(data)
df.plot(kind='bar', color='g')
plt.grid()
plt.show()

data = {'дискретный сигнал x(n)': x_n}
df = pd.DataFrame(data)
df.plot(kind='bar', color='b')
plt.grid()
plt.show()

data = {'реакция y(n)': y_n}
df = pd.DataFrame(data)
df.plot(kind='bar', color='r')
plt.grid()
plt.show()

Результаты выполнения:
Реакция системы:

[6, 8, 15, 18, 28, 38, 45, 54, 51, 56, 54, 46, 40, 31, 19, 13, 4, 2, 0, 0]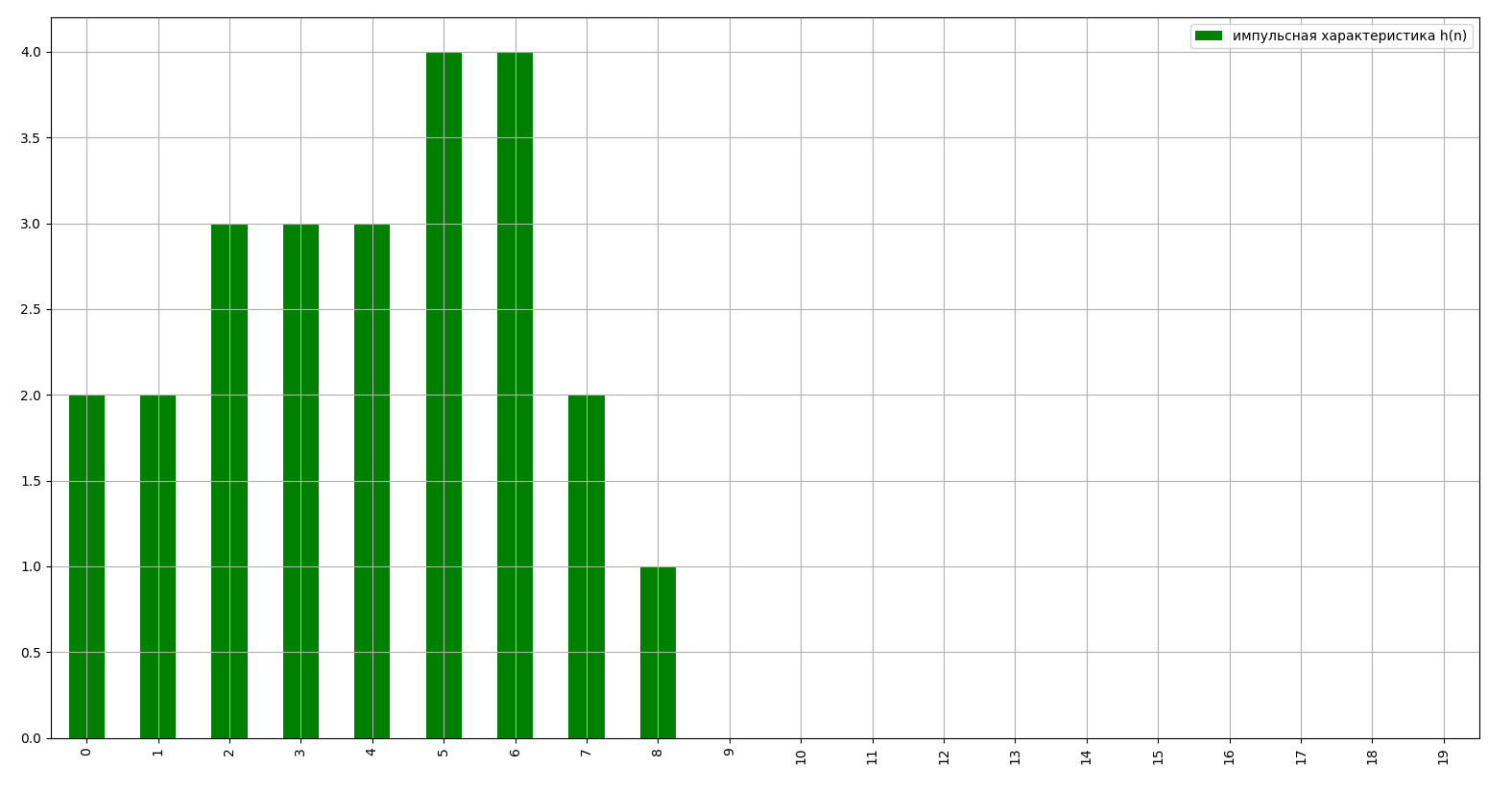

Рис.№1. Импульсная характеристика системы.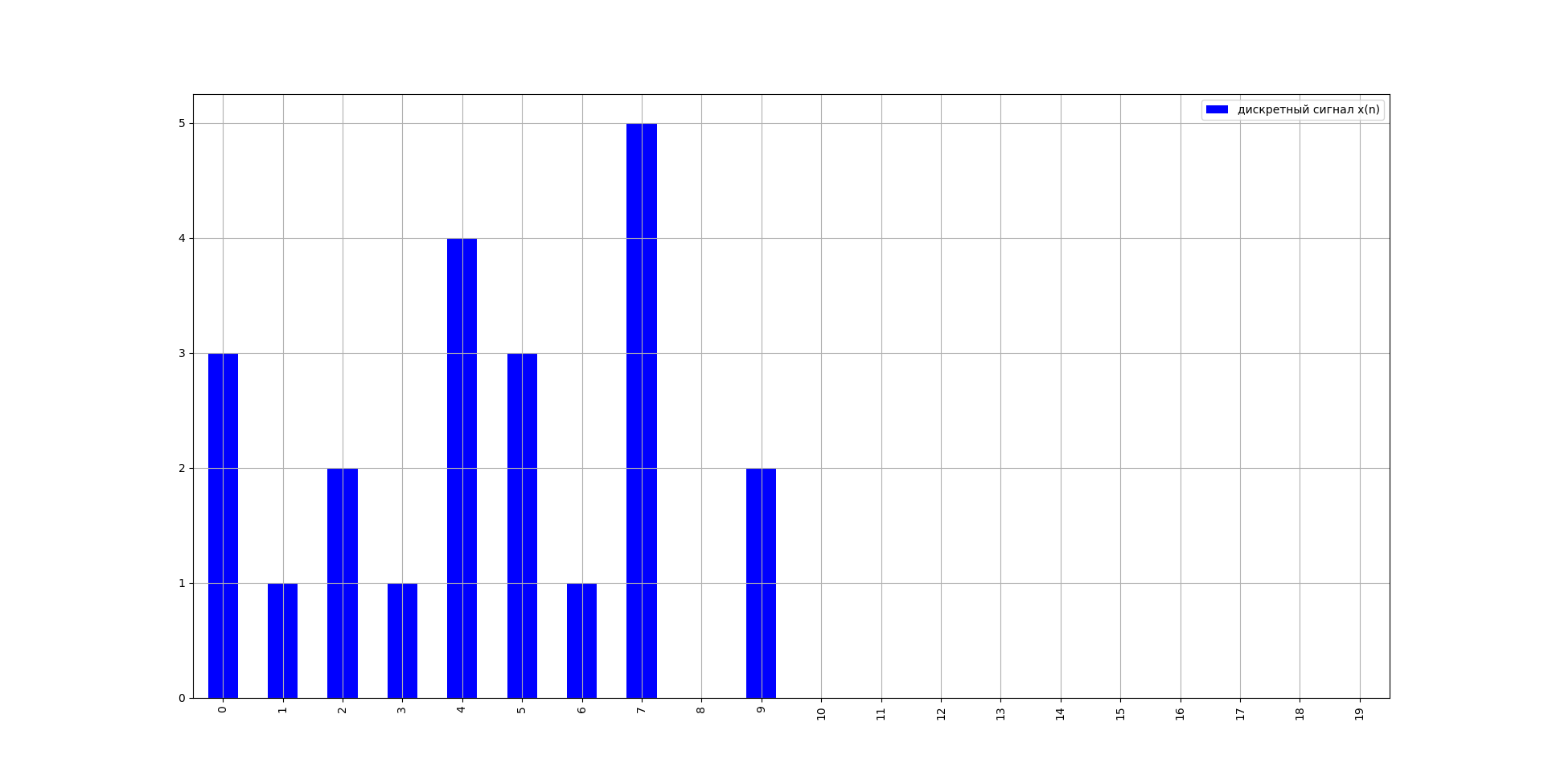

Рис.№2. Входной сигнал.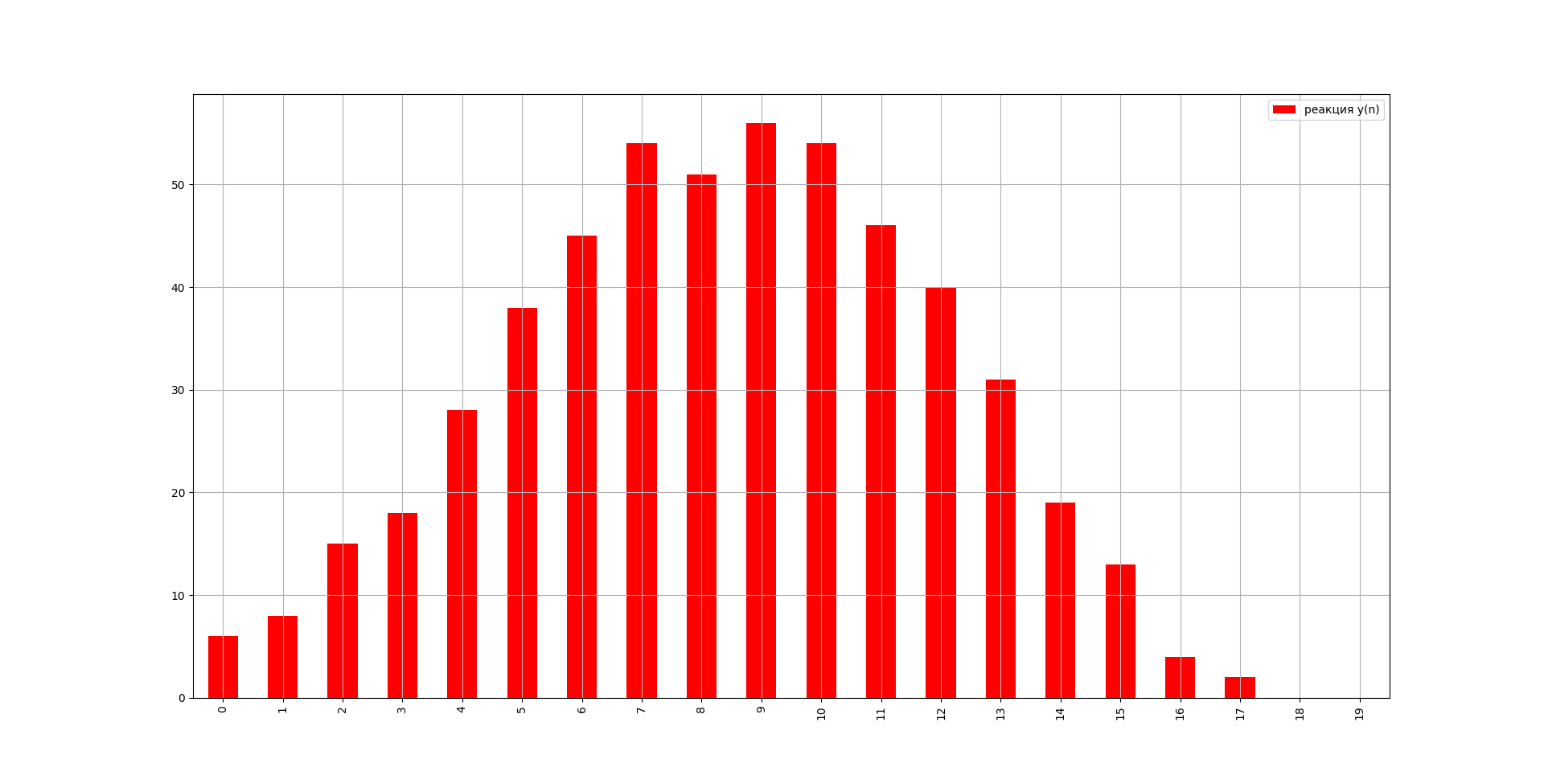

Рис.№3. Реакция системы.

ВЫВОД: в результате выполнения данной лабораторной работы была рассчитана реакция линейной дискретной системы на произвольное воздействие с использованием формулы свертки.