Лабораторная работа 1 Построение истинных диаграмм деформирования по результатам испытаний образцов на осевое растяжение
 Скачать 44.86 Kb. Скачать 44.86 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Федеральное государственное автономное образовательное учреждение высшего образования «Нижегородский государственный университет им. Н.И. Лобачевского» Национальный исследовательский университет Институт информационных технологий, математики и механики Кафедра теоретической, компьютерной и экспериментальной механики Лабораторная работа №1 «Построение истинных диаграмм деформирования по результатам испытаний образцов на осевое растяжение» Выполнили: Барышникова Наталья Жучкова Алёна Ильина Марина Ларин Захар Столярова Дарья Проверил: Леонтьев Н. В. Н. Новгород 2019 Перед началом испытания измерили Средний диаметр подсчитывали по формуле: Таблица 1
Таблица 2
Находим Δ Модуль упругости первого рода определяем по формуле: E= где B - база тензометра. После окончания испытания измерили минимальный диаметр в шейке образца Таблица 3
Исходя из первичной диаграммы растяжения сняли значения усилий 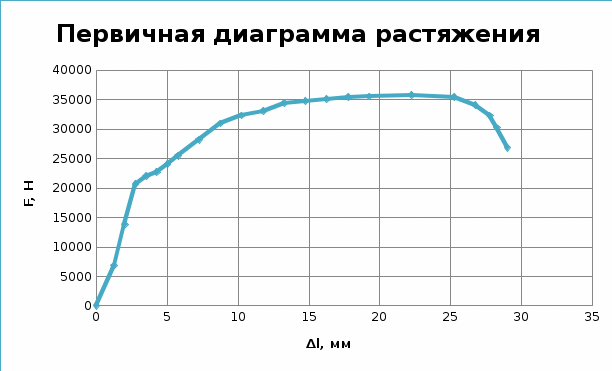 Значения условных напряжений и деформаций, подсчитанных по формулам: занесли в табл.4. Далее строим вторичную условную диаграмму напряжений в осях Значение относительной упругой деформации находим по формуле: Считаем коэффициент Пуассона для точек диаграммы, расположенных между пределом упругости и временным сопротивлением, приняв, что до предела упругости для стали ν= Построили диаграмму зависимости 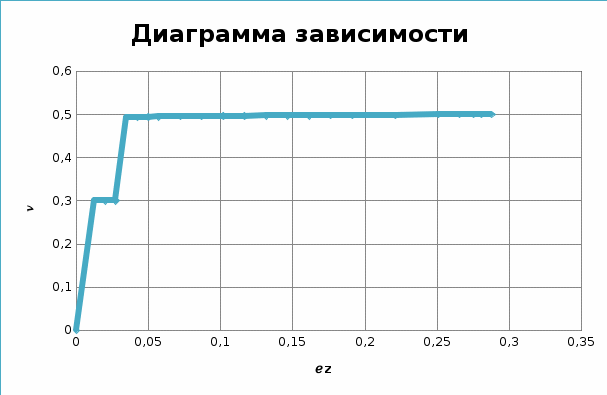 Истинные напряжения и деформации считаем по формулам: Истинные напряжения и деформации считаем по формулам:По посчитанным значениям . 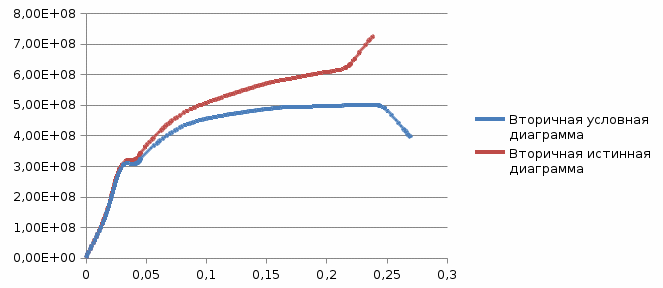 До момента образования шейки интенсивность напряжений и деформаций равна: Для точки, соответствующей разрушению образца: По результатам вычислений построили истинную диаграмму деформирования. 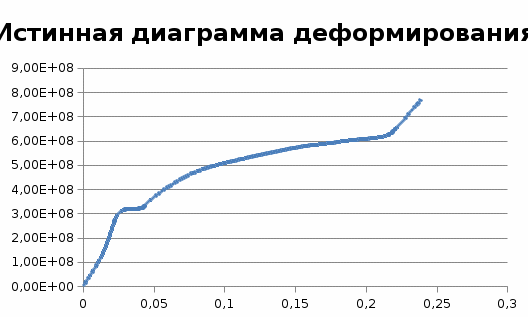 Таблица 4. |
