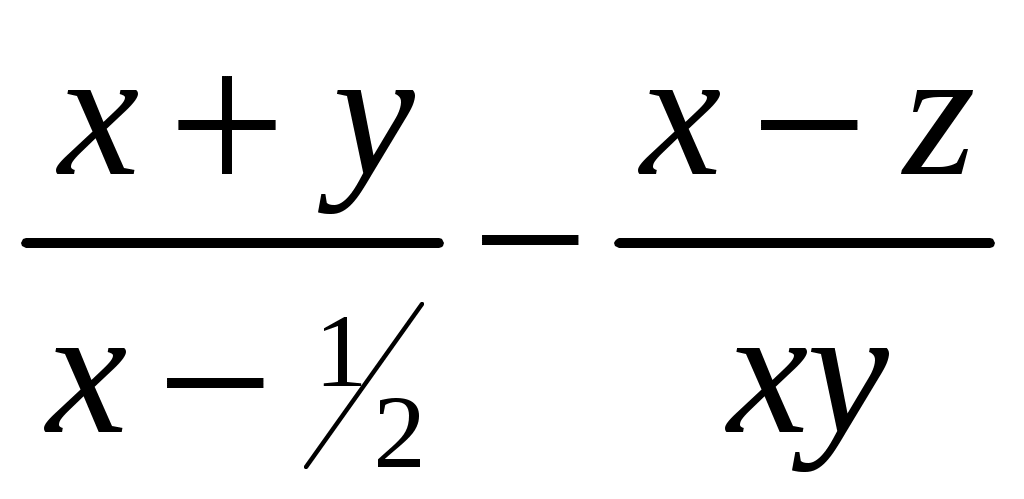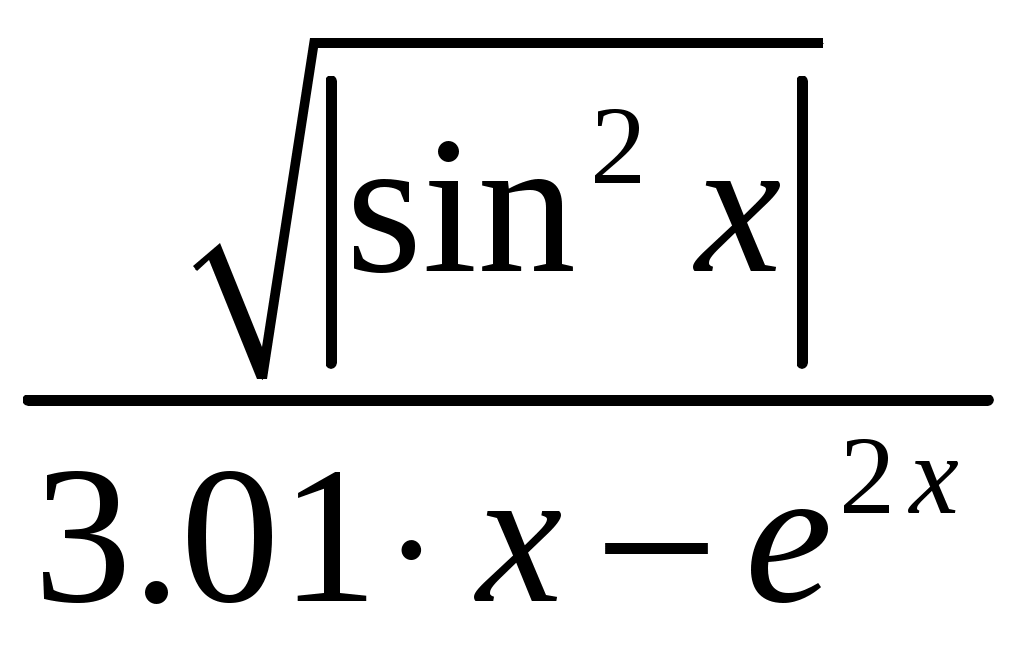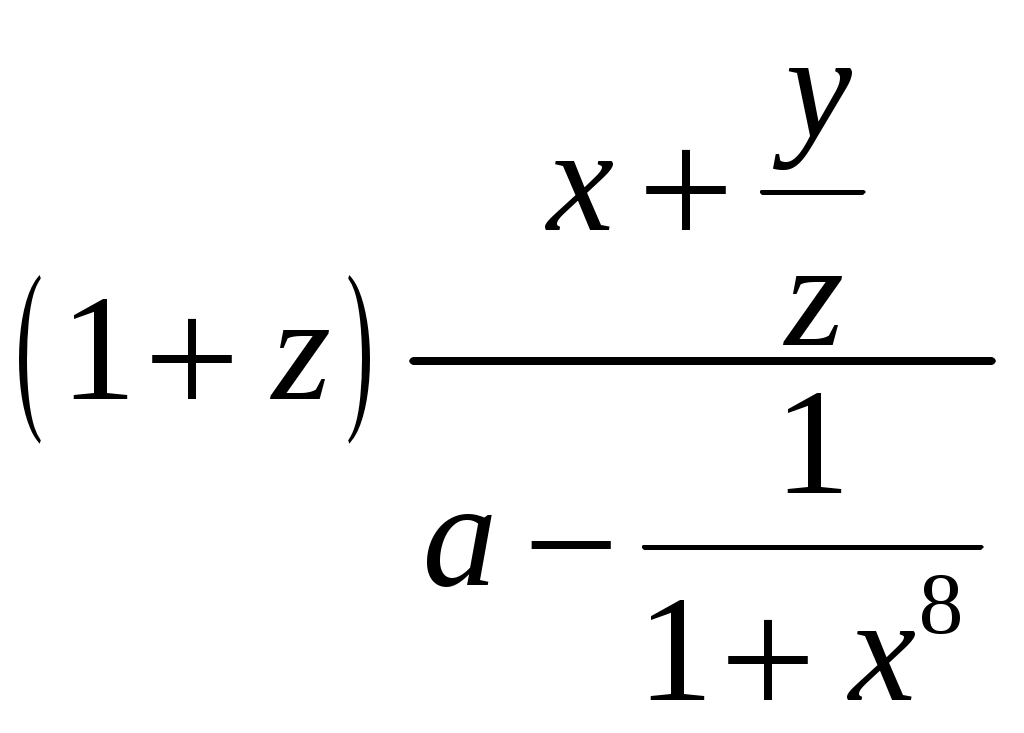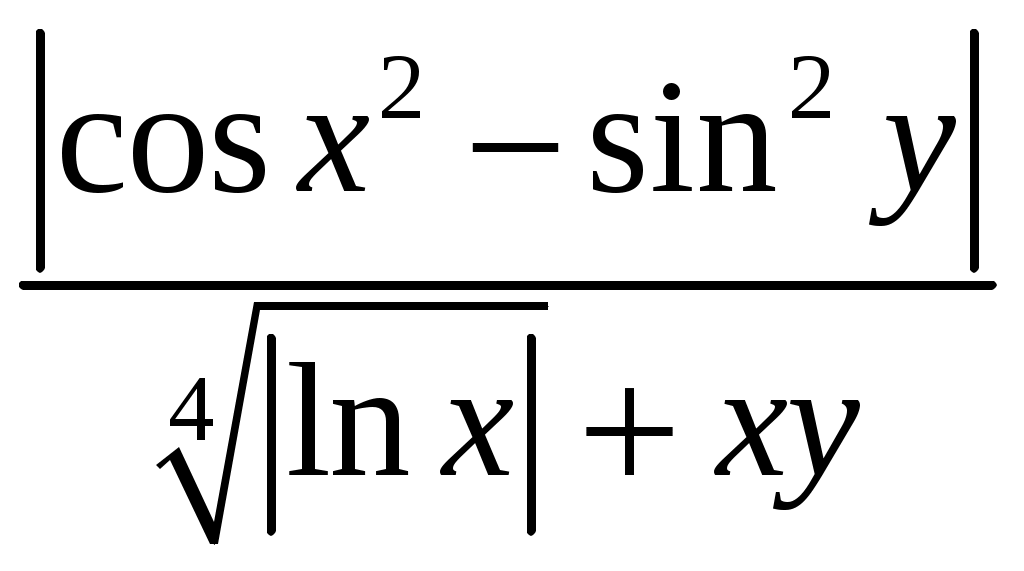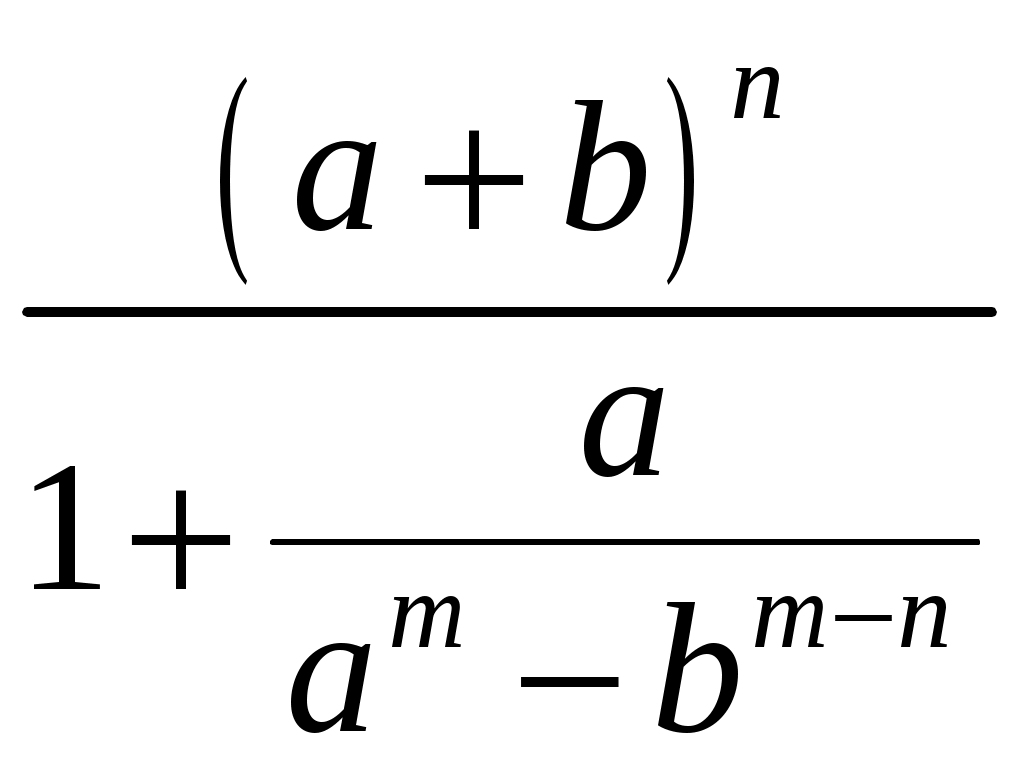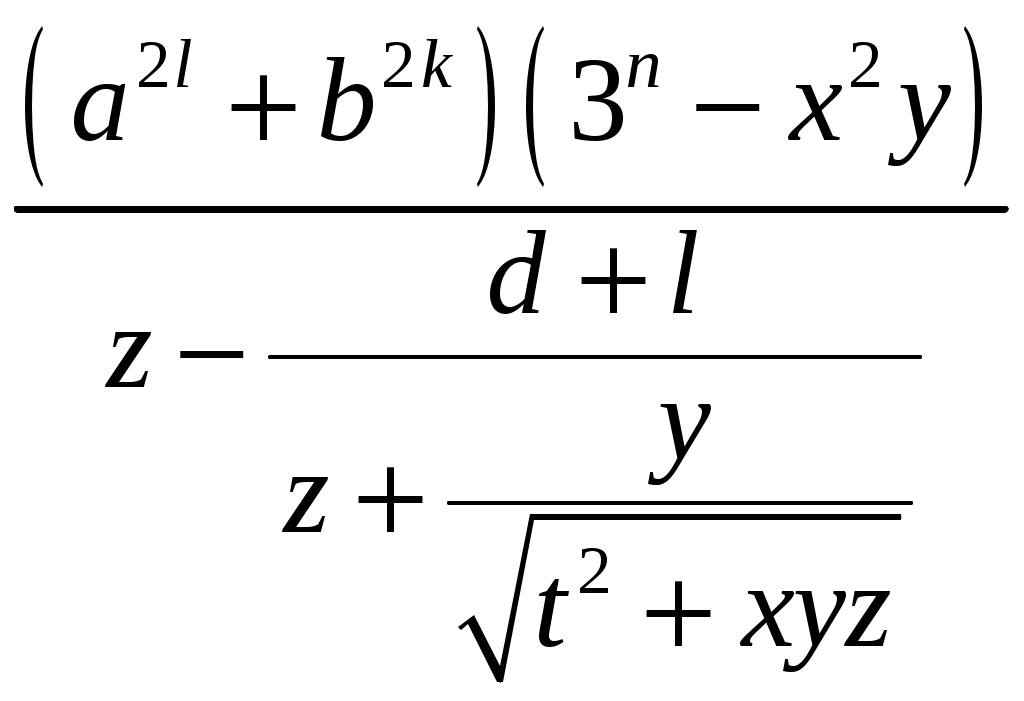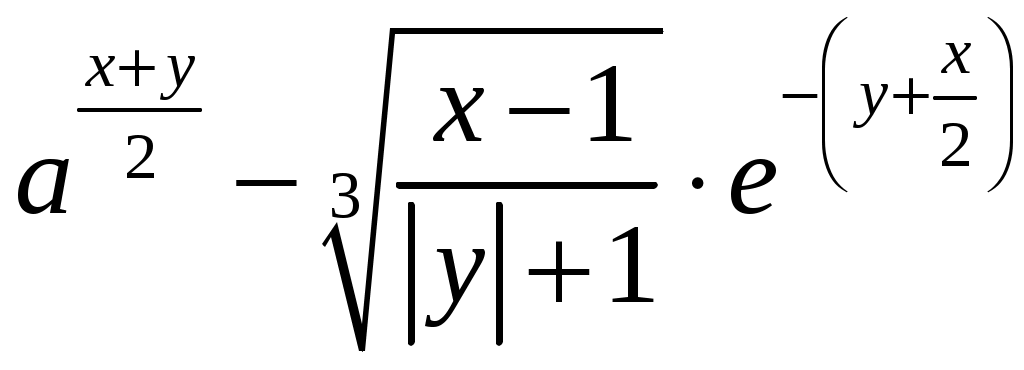Главная страница
Навигация по странице:

  • Задания для выполнения по вариантам: Задание 1

    		•

    да. 1_ПУ_Линейные алгоритмы. Лабораторная работа 1 Практика на эвм 1 курс, специальность Фундаментальная информатика и информационные технологии


    Скачать 194.5 Kb.
    НазваниеЛабораторная работа 1 Практика на эвм 1 курс, специальность Фундаментальная информатика и информационные технологии
    Дата20.12.2020
    Размер194.5 Kb.
    Формат файлаdoc
    Имя файла1_ПУ_Линейные алгоритмы.doc
    ТипЛабораторная работа
    #162343

    Лабораторная работа №1 Практика на ЭВМ

    1 курс, специальность «Фундаментальная информатика и информационные технологии»


    Линейные алгоритмы

    Задания для выполнения по вариантам:

    Задание 1. Найдите значение выражения:

    1


    6


    2


    7


    3


    8


    4


    9


    5


    10


    Задание 2. Составить программу для определения указанных ниже параметров:

    Переводы

    1. Угол задан в градусах, минутах и секундах. Найти его величину в радианах (с максимально возможной точностью).

    2. Решить задачу, обратную предыдущей, то есть перевести заданную величину угла из радианной меры в градусную.

    3. Длина задана в дюймах (1 дюйм = 2,54 см). Перевести ее в метрическую систему, то есть выразить в метрах, сантиметрах и миллиметрах.

    4. Заданы моменты начала и конца некоторого периода времени в часах, минутах и секундах. Найти продолжительность этого периода в том же виде (в пределах одних суток). Тип данных Data использовать нельзя.

    5. Русские не метрические единицы длины: 1 верста = 500 саженей; 1 сажень = 3 аршина; 1 аршин = 16 вершков; 1 вершок = 44,45 мм. Длинна некоторого отрезка составляет р метров. Перевести её в русскую не метрическую систему.

    6. Текущее время (часы, минуты, секунды) задано тремя переменными: , , . Округлить его до целых минут и до целых часов. Например, 14 час. 21 мин. 45 с. преобразуется в 14 час. 22 мин. или 14 час., а 9 час. 59 мин. 23 с. - соответственно в 9 час. 59 мин. или 10 час.

    7. Перевести сумму заработанных денежных средств из рублей в евро.

    8. Решить задачу, обратную предыдущей, то есть перевести сумму заработанных денежных средств из евро в рубли.

    9. Задана температура в градусах. Найти ее величину в фаренгейтах.

    Температура по шкале Фаренгейта связана с температурой по шкале Цельсия формулами: , .

    1. Решить задачу, обратную предыдущей, то есть перевести значение температуры из фаренгейтов в градусы.

    Фигуры

    1. У квадрата ABCD на плоскости известны координаты двух противоположных вершин – точек А и С. Найти координаты двух остальных точек B и D.

    2. В равнобедренном прямоугольном треугольнике известна высота h, опущенная на гипотенузу. Найти стороны треугольника.

    3. Треугольник АВС задан длинами своих сторон. Найти длины высот, опущенных из вершин.

    4. Из круга радиусом r вырезан прямоугольник, большая сторона которого равна a. Круг какой площади можно вырезать из полученного прямоугольника?

    5. Найти площадь треугольника АВС, заданного координатами своих вершин на плоскости.

    6. Найти сумму длин медиан треугольника АВС, заданного координатами своих вершин на плоскости.

    7. Найти координаты центра окружности, вписанной в треугольник АВС (задан координатами своих вершин на плоскости).

    8. Найти внутренние углы (в градусах) треугольника АВС, заданного координатами своих вершин на плоскости.

    9. Найти точку D, симметричную точке А относительно стороны ВС треугольника АВС, заданного координатами своих вершин на плоскости.

    10. Найти внешние углы треугольника АВС, заданного длинами своих сторона плоскости.

    Задачи прикладного характера (по две задачи, например, 3 и 13, 7 и 17, 5 и 15)

    1. Заданы три корня кубического уравнения: , , . Найти коэффициенты этого уравнения.

    2. Найти корни квадратного уравнения, заданного своими коэффициентами, с положительным дискриминантом; подстановкой в уравнение убедиться в погрешности вычислений.

    3. Заданы действительная и мнимая части комплексного числа . Преобразовать его в тригонометрическую форму и напечатать в виде выражения:

    .

    1. Заданы уравнения двух пересекающихся прямых на плоскости: ; . Найти (в градусах и минутах) угол между ними.

    2. Заданы координаты точки подвески маятника и координаты одной из точек его наивысшего подъема . Найти координаты самой низкой точки траектории и другой наивысшей точки подъема.

    3. Найти угол (в градусах) между векторами и , заданных своими координатами на пространстве.

    4. Найти объем пирамиды, построенной на векторах , , , как на сторонах. Вектора заданы своими координатами в пространстве.

    5. Найти длину диагонали параллелепипеда, построенного на векторах , , , как на сторонах. Вектора заданы своими координатами в пространстве.

    6. На тело действуют две силы, заданные векторами и . Найти величину и направление (углы с координатными осями) их равнодействующей. Вектора заданы своими координатами в пространстве.

    7. В такси одновременно сели три пассажира. Когда вышел первый пассажир, на счетчике было рублей; когда вышел второй – рублей. Сколько должен заплатить каждый пассажир, если по окончании поездки счетчик показал рублей? Плата за посадку составляет рублей.

    8. Коммерсант, имея стартовый капитал рублей, занялся торговлей, Которая ежемесячно увеличивает капитал на . Через сколько лет он накопит сумму , достаточную для покупки собственного магазина?

    9. Селекционер вывел новый сорт зерновой культуры и снял с опытной делянки кг семян. Посеяв 1 кг семян, можно за сезон собрать кг. Через сколько лет селекционер сможет засеять новой культурой поле площадью га, если норма высева кг/га?

    10. За первый год производительность труда на предприятии возросла на процентов, за второй и третий – соответственно на и процентов. Найти среднегодовой прирост производительности (в процентах).

    11. Владелец автомобиля приобрел новый карбюратор, который экономит 50% топлива, новую систему зажигания, которая экономит 30% топлива, и поршневые кольца, экономящие 20% топлива. Верно ли, что его автомобиль теперь сможет обходиться совсем без топлива? Найти фактическую экономию для произвольно заданных процентов.

    12. Животновод каждую зиму повышает отпускную цену на молоко на %, а каждое лето – снижает на столько же процентов. Изменится ли через лет цена на молоко и если да, то в какую сторону и на сколько?

    13. Годовой план Леспромхоз ведет заготовку деловой древесины. Ее первона­чальный объем на территории леспромхоза был равен м3. Ежегодный прирост составляет %. Годовой план заготовки древесины – м3. Какой объем деловой древесины на данной территории будет через год, через два и т.д., пока этот объем не станет меньше минимального значения м3?

    14. Путник двигался часов со скоростью , затем часов – со скоростью и часов – со скоростью . За сколько часов он одолел первую половину пути?

    15. Длины сторон первого прямоугольника и , его площадь в 6 раз меньше площади второго прямоугольника. Найти длину стороны второго прямоугольника, если длина одной из его сторон равна .

    16. Длина стороны треугольника равна , периметр равен , длины двух других сторон равны между собой. Найти эти длины.

    17. Пароход плыл от пункта А в пункт В по течению реки часов, а возвращался – часов. Найдите скорость парохода в стоячей воде и скорость течения реки, если известно, что скорость течения реки на 3 м/с меньше скорости парохода.

    написать администратору сайта