курсовая. курс.р1. Лабораторная работа 1 "Простейшие вычисления в Matchcad". Построение декартова графика
 Скачать 339.44 Kb. Скачать 339.44 Kb.
|
1 2 Лабораторная работа №1 "Простейшие вычисления в Matchcad". Построение декартова графика. Для того, чтобы построить декартов график какой-либо функции нужно установить курсор в том месте документа, где должен находиться график, и вставить шаблон декартова графика с помощью соответствующей кнопки на панели инструментов Графики. 2. Построение графика в полярной системе координат. Для вставки шаблона полярного графика выберите команду меню Вставка→График→Полярные координаты или щелкните на соответствующей кнопке панели инструментов Графики. Форматирование полярного графика производится аналогично форматированию декартова графика. 3. График параметрически заданной функции. Кроме явного задания функции, существует параметрическое задание функции, при котором указывается зависимость обеих координат от некоторого параметра. В MathCAD можно построить такую функцию, если ввести в оба поля ввода функции, зависящие от одного параметра. 4. Построение трехмерного графика в виде поверхности. Для построения графика функции z(x,y) в виде трехмерной поверхности нужно сначала задать эту функцию , а затем вставить шаблон поверхностного графика (команда меню Вставка→График→Поверхности или соответствующая кнопка на панели инструментов Графики), введя в его поле ввода имя заданной функции z. 5. Построение правильных многогранников. Для построения правильных многогранников в MathCAD существует встроенная функция Polyhedron(S). Аргументом данной функции должна быть строка, задающая либо порядковый номер многогранника (при этом перед числом обязательно должен стоять символ #), либо его имя, либо его код, описывающий правило построения многогранника. 1.  , голубой , голубой , коричневый , коричневый 2.  , ,    3.   4. Построить правильный многогранник с порядковым номером своего варианта умноженный на 33.    Лабораторная работа № 2 "Способы символьных вычислений" Символьные вычисления в MathCAD можно осуществлять в двух различных вариантах: - с помощью команд меню; - с помощью оператора символьного вывода ->, ключевых слов символьного процессора и обычных формул. Первый способ более удобен, когда требуется быстро получить какой-либо аналитический результат для однократного использования, не сохраняя сам ход вычислений. Второй способ более нагляден, т. к. позволяет записывать выражения в традиционной математической форме и сохранять символьные вычисления в документах MathCAD. Первый способ (с помощью меню). 1. Введите выражение sin (2х). 2. Выделите его целиком . 3. Выберите в главном меню пункты Symbolics / Expand (Символика / Разложить). После этого результат разложения выражения появится чуть ниже в виде еще одной строки. Символьные операции с помощью меню возможны лишь над каким-либо объектом (выражением, его частью или отдельной переменной). Для того чтобы правильно осуществить желаемое аналитическое преобразование, предварительно необходимо выделить тот объект, к которому оно будет относиться. Второй способ символьных преобразований (с помощью оператора ->). 1. Введите выражение sin (2х). 2. Нажмите кнопку Expand (Разложить) на панели Symbolic (Символика). 3. Введите в местозаполнитель после появившегося ключевого слова expand имя переменной х, либо нажмите клавишу 4. Введите оператор символьного вывода (->) 5. Нажмите клавишу Если символьные вычисления осуществляются вторым способом, символьный процессор учитывает все формулы, предварительно введенные в документе . Например,  1.Стороны треугольника 76, 32, 56 cos(2x) +sin(2x)tg(x) 7935   4.  5. 9+(3-z)y-2y(x+4y)  6. Лабораторная работа №3 "Матричные вычисления" Способы задания матрицы. Матрицу можно целиком ввести с клавиатуры, либо с помощью функциональной зависимости элемента массива от его индексов. 1.1 Введение элементов матрицы с клавиатуры Для того чтобы ввести элементы матрицы с клавиатуры, выберите команду меню Insert →Matrix или на панели инструментов Matrix щелкните на кнопке Matrix or Vector. В открывшемся диалоговом окне введите количество строк (Rows) и столбцов (Columns). При нажатии клавиши OK появится шаблон матрицы, в который можно вводить ее элементы. Это же диалоговое окно (Insert Matrix или Вставить Матрицу ) позволяет добавлять и удалять несколько строк и столбцов в уже имеющейся матрице. Для того, чтобы добавить строки и столбцы в матрицу, установите курсор на элемент матрицы, справа от которого вы хотите вставить столбцы и ниже которого вы хотите вставить строки. Введите количество вставляемых строк и столбцов и щелкните на кнопке Insert (Вставить).Например 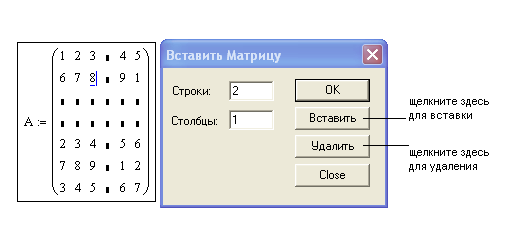 1.2 Задание матрицы, элементы которой являются функциями индексов. Например, для того, чтобы задать матрицу A размером 4х 5 , каждый элемент которой равен сумме номера строки и удвоенного номера столбца, то нужно задать переменные диапазона i:=1..4 , j:=1..5 и задать формулу Ai,j:=i+2k. Можно задать такую матрицу без использования переменных диапазона, с помощью специальной функции matrix(4,5,f), описав заранее функцию f. Например: 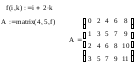 1.                  Лабораторная работа № 4 "Решение уравнений и систем уравнений." Численный поиск корня уравнения. Любой численный метод решения уравнения основан на уточнении какого-либо начального значения корня до заданной точности. Точность вычислений в MathCAD задается встроенной переменной TOL и по умолчанию равна 0,001. Для задания начального значения корня удобно сначала построить график функции, задающей уравнение. Например, найдем корни уравнения 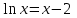 . .2. Нахождение корней полиномов. Для нахождения корней полинома в MathCAD имеется встроенная функция polyroots(a), аргументом которой является вектор коэффициентов полинома 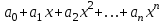 . .3. Нахождение корней уравнений аналитически (путем символьных преобразований). Во многих случаях MathCAD позволяет найти аналитическое решение. Для того, чтобы найти решение уравнения необходимо записать выражение и выделить в нем переменную (поставить указатель курсора возле переменной), и воспользоваться пунктом Solve for Variable (ПеременнаяРешение ) из пункта меню Symbolic (Символика). 4. Численный поиск решения системы уравнений и неравенств. Системы линейных и нелинейных уравнений и неравенств позволяет решать в MathCAD блок given в сочетании с функцией Find. После слова given записывается система уравнений и неравенств, подлежащих решению, при этом вместо знака «=» следует набирать Ctrl+=. Перед блоком given необходимо указывать начальные приближения для всех переменных, если нужно найти комплексный корень, то следует задавать комплексное начальное приближение. Признаком окончания системы служит функция Find, если надо найти точное решение или функция Minerr, если система не может быть решена точно, и требуется найти наилучшее приближение, обеспечивающее минимальную погрешность. 5. Решение систем линейных уравнений. Систему линейных уравнений можно решать численным методом, описанном в предыдущем пункте, но если определитель матрицы из коэффициентов при неизвестных в уравнениях системы будет равен 0 (система не имеет решения либо имеет множество решений), то численный метод не даст результата. Также численный метод может дать приближенный результат вместо точного. Поэтому для решения систем линейных уравнений можно воспользоваться методом Гаусса, матричным методом или формулами Крамера. Однородную же систему линейных уравнений можно решить только методом Гаусса. 6. Решение систем уравнений в символьном виде. Во многих случаях решение системы уравнений может быть найдено не только численно, но и аналитически. Для этого также используется блок given и функция Find, но вместо знака равенства после функции следует поставить знак символического преобразования . 1.  2.   3. 4.  6. Б.                График 5 задание  1 2 |
