лр 1. Лабораторная работа 1 расчет погрешностей при измерении объема цилиндра
 Скачать 46.46 Kb. Скачать 46.46 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1.1 РАСЧЕТ ПОГРЕШНОСТЕЙ ПРИ ИЗМЕРЕНИИ ОБЪЕМА ЦИЛИНДРА ЦЕЛЬ РАБОТЫ: ознакомление с простейшими физическими измерениями, определение объема цилиндра и расчет погрешностей прямых и косвенных измерений. ЗАЧЕТНЫЙ МИНИМУМ: 1. Физическая величина – это характеристика одного из свойств физического объекта (явления или процесса), общая в качественном отношении многим объектам, но в количественном отношении индивидуальная для каждого объекта. Значение физической величины – это оценка ее величины в виде некоторого числа принятых для нее единиц или числа по принятой для нее шкале. 2. Измерением физической величины называют совокупность операций, выполняемых с помощью технического средства, хранящего единицу или воспроизводящего шкалу физической величины, заключающихся в сравнении (в явном или неявном виде) измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, удобной для использования. 3. Штангенциркуль – высокоточный инструмент, используемый для измерения наружных и внутренних линейных размеров, глубин отверстий и пазов, разметки. Свое название этот универсальный прибор получил от линейки-штанги, которая служит основой его конструкции. Штанга с основной шкалой в мм. неподвижные губки расположены на штанге. рамка с подвижными губками и жестко соединенным с ней глубинометром. Зажимной винт. Нижние измерительные губки – для наружных размеров. Верхние измерительные губки – для внутренних размеров. Шкала «нониус» - расположена на скошенной грани рамки Для измерения десятых долей миллиметра служит вспомогательная шкала, называемая нониусом, длина которого равна 19 мм и поделена на десять делений. При измерении штангенциркулем целое число миллиметров отсчитывают по миллиметровой шкале штанги, а десятые доли миллиметра по шкале Нониуса, начиная от нулевой отметки до той риски, которая совпадает с какой-либо риской шкалы штанги. Это и будет число десятых долей миллиметра. 4. Измерительный прибор высокой степени точности, позволяющий определять линейные размеры физических тел, называется микрометр. В начале работы необходимо расположить измерительную деталь между пяткой прибора и микрометрическим винтом. Начать вращение барабана с учетом максимальной близости шпинделя и измеряемого предмета. Во избежание нагрева от температуры тела и искажения результатов держать прибор следует за изолированную часть скобы. Размеренно и не спеша до соприкосновения с измеряемой поверхностью подводится шпиндель устройства. Крутить его следует по направлению против часовой стрелки относительно торца с нарезкой пока деталь не зайдет в зазор торцов. Далее, необходимо по часовой стрелке довести вращение шпинделя до упора, придерживая в процессе нарезки барабан. При достижении упора вращение начнет сопровождаться треском. Вращение микрометрического винта следует прекратить и можно приступать к снятию показаний. Освобождается деталь из зажима обратным вращением шпинделя. Точный размер замеряется на барабане с помощью шкалы нониуса. Начинаем снимать показания с более крупного разряда цифр и оканчиваем мелким. 5. Правила приближенных вычислений.При вычислениях чаще всего проводят алгебраические действия не с точными величинами, а с их приближенными значениями. При этом руководствуются следующими правилами. В записи приближенного числа с помощью десятичной дроби оставляют только верные знаки. При сложении или вычитании приближенных чисел в результате (в сумме или разности) необходимо оставлять столько десятичных знаков, сколько их дано в компоненте с наименьшим числом этих знаков. При умножении и делении приближенных чисел в результате (произведении или частном) оставляют столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр. 6. Если тело имеет геометрически правильную форму (шар, призма, цилиндр, конус и т.д.), то его объем легко вычисляется математически. Необходимые линейные размеры определяются с помощью штангенциркуля и микрометра. 7. Под измерением понимают сравнение измеряемой величины с другой величиной, принятой за единицу измерения. Измерения выполняются опытным путем с помощью специальных технических средств. Прямыми измерениями называются измерения, результат которых получается непосредственно из опытных данных (например, измерение длины линейкой, времени – секундомером, температуры – термометром). Косвенными измерениями называются измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, значения которых получают в процессе прямых измерений Систематические погрешности – это погрешности, величина которых одинакова во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов, в одних и тех же условиях. Систематические погрешности происходят: - в результате несовершенства приборов, используемых при измерениях (например, стрелка амперметра может быть отклонена от нулевого деления в отсутствие тока; у коромысла весов могут быть неравные плечи и др.); - в результате недостаточно полной разработки теории метода измерений, т. е. метод измерений содержит в себе источник ошибок (например, возникает ошибка, когда в калориметрических работах не учитывается потеря тепла в окружающую среду или когда взвешивание на аналитических весах производится без учета выталкивающей силы воздуха); Случайные погрешности – это погрешности, величина которых различна даже для измерений, выполненных одинаковым образом. Причины их кроются как в несовершенстве наших органов чувств, так и во многих других обстоятельствах, сопровождающих измерения, и которые нельзя учесть заранее Существуют две методики расчета погрешностей случайной величины. Методика прямых измерений и методика косвенных измерений ( РМГ-76-2014) ОБОРУДОВАНИЕ: штангенциркуль с ценой деления 0,05 мм, микрометр с ценой деления 0,01 мм, цилиндрическое тело. Расчетная формула V 1 d 2 h, 4 где D - диаметр цилиндра; H - высота цилиндра. Объем цилиндра линейно зависит от его высоты, и прямоквадратичная зависимость от диаметра его основания. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Измерили по пять раз штангенциркулем диаметр цилиндра D, микрометром высоту цилиндра H. Результаты измерений запишите в таблицу 1. Таблица 1 – Результаты измерений
2. Определили абсолютные погрешности Di = D Di и квадрат абсолютной погрешности ( Di)2 = D Di 2, а также сумму ( Di)2 и записали результат в таблицу 1. 3. Определите Hi = H Hi и ( Hi)2 = H Hi2, а также сумму и все результаты записали в таблицу 1. 4. Вычисляем приближенное значение объема цилиндра: 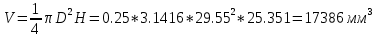 5. Оценка погрешности прямых измерений Приборные погрешности D = 0,05 мм = 5 10 2 (мм); Приборные погрешности H = 0,005 мм = 5 10 3 (мм); Средние квадратичные отклонения средних арифметических отклонений (стандартный доверительный интервал): 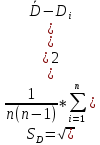 = 2.41.10-2 мм = 2.41.10-2 мм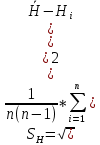 = = 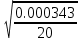 = 4,14.10-3 мм = 4,14.10-3 ммПримем доверительную вероятность = 0,95. При n = 5 коэффициент Стьюдента tn = 2,776. Тогда случайные ошибки при измерениях диаметра и высоты цилиндра будут равны: 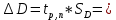 2.776 * 2.41.10-2 мм = 6.67.10-2 мм 2.776 * 2.41.10-2 мм = 6.67.10-2 мм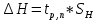 = 2.776 * 4,14.10-3 мм = 1.15.10-2 мм = 2.776 * 4,14.10-3 мм = 1.15.10-2 ммСуммарные погрешности величин D и H: 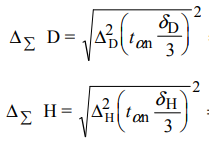 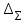 D = D = 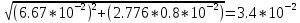 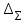 H = H = 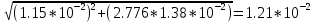 6. Оценка абсолютной погрешности косвенного измерения объема цилиндра 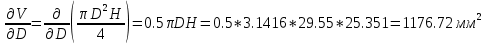 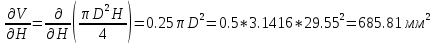 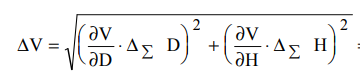 ∆V = 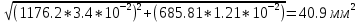 На основании расчетов получено: V = 17386 40.9 мм3. Представим полученный результат в общепринятом виде. Результат для V записываем с одной сомнительной цифрой, после которой неверные цифры заменяем нулями. Погрешность этого округления прибавляем к предельной абсолютной погрешности V = 386 + 40.9 = 426.9 (мм3). Предельную абсолютную погрешность округляем до одной значащей цифры Окончательно имеем V 400 (мм3). V = 17000 400 (мм3) или V = (17 0,4) 103 (мм3). Относительная погрешность составляет 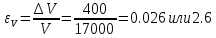 Запись окончательного результата V = (17 0,4) 103 (мм3) с = 0,95 и Е = 2,6 %. Выводы В результате проведенного лабораторного эксперимента объем цилиндра V = (17 0,4) 103 (мм3) с надёжность 95 % при числе измерений n= 5 и относительной погрешности 2,6 % . Экспериментальное определение объема связано со случайными и систематическими погрешностями измерений. |

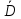 =29,55
=29,55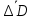 =29,55
=29,55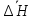 =0.0066
=0.0066