Дискретная математика. Лабораторная работа 1 Реализация операций над подмножествами заданного универсума
 Скачать 149.47 Kb. Скачать 149.47 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ Кафедра «АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ»  Лабораторная работа 1 «Реализация операций над подмножествами заданного универсума» Вариант 6 Выполнил: студент гр. МиРр-191 Кулешов Даниил Николаевич Проверил: Доктор технических наук, доцент Якимов А.И. Могилев, 2020 Цель работы: изучение реализации операций над подмножествами заданного универсума. Ход работы Ваш вариант №14 Задание 1.1 Его и надо выполнить 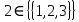 – верно, т.к. 2 – верно, т.к. 2 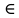 множеству множеству 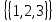 Ответ неверный Ответ неверный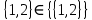 – верно, т.к. {1,2} является подмножеством {{1,2}} => и принадлежит ему – верно, т.к. {1,2} является подмножеством {{1,2}} => и принадлежит ему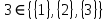 – верно, т.к. 3 – верно, т.к. 3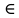 множеству множеству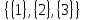 Ответ неверный Ответ неверныйЗадание 1.2 Ваш вариант №14 Его и надо выполнить 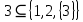 – неверно, 3 не является множеством – неверно, 3 не является множеством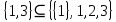 – верно, т.к. 1,3 принадлежат обоим множествам – верно, т.к. 1,3 принадлежат обоим множествам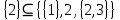 – верно, т.к. 2 принадлежит обоим множествам – верно, т.к. 2 принадлежит обоим множествамЗадание 1.3 Ваш вариант №14 Его и надо выполнить 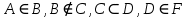 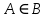 |A = {1,2}, B = {{1,2},3} |A = {1,2}, B = {{1,2},3}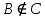 | B = {{1,2},3}, C = {5,6,7} | B = {{1,2},3}, C = {5,6,7}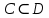 | C = {5,6,7}, D = {5,6,7,8} | C = {5,6,7}, D = {5,6,7,8}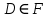 | D = {5,6,7,8}, F = {{5,6,7,8}, 7, 8} | D = {5,6,7,8}, F = {{5,6,7,8}, 7, 8}Задание 1.4 Ваш вариант №14 Его и надо выполнить Если 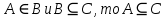 Все объекты множества А принадлежат множеству В, в то время как множество В является подмножеством множества С => множество А также содержится в множестве С Утверждение верное, например: A = {1}, B = {{1}, 2}, C = {{1}, 2, 3} Остальные задания выполнять не надо. Задание 1.5 A = {1, {2}, 3} 2A = {{∅},{1}, {{2}}, {3}, {1,{2}}, {1, 3}, {{2}, 3}, {1,{2}, 3}} Задание 1.6 (A∆B) ∩ (D∪ 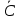 ) )E = {1,2,3,4,5,6,7,8,9,10} A = {1,3,5,6} B = {1,2,3,5,7} C = {2,5,7,8} D = {1,4,7,9,10} A∆B = {2,6,7} 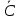 = {1,3,4,6,9,10} = {1,3,4,6,9,10}(D∪ 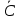 )={1,3,4,6,7,9,10} )={1,3,4,6,7,9,10}(A∆B) ∩ (D∪ 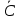 )={6,7} )={6,7}Задание 1.8 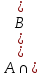 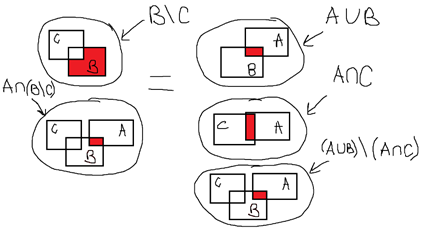 Верно Вывод: выполненные исследования подтверждают справедливость утверждений теории множеств |
