Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы
 Скачать 454.13 Kb. Скачать 454.13 Kb.
|
|
Вариант2 Для строительства трех объектов используется кирпич, изготовляемый на трех заводах. Ежедневно каждый из заводов может изготовлять 100, 150 и 50 уcл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектах соответственно равны 75, 80, 60 и 85 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого с заводов к каждому из строящихся объектов: 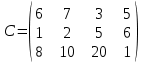 Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной. Вариант3 На трех железнодорожных станциях скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции В1, В2, ВЗ, В4 и В5. На каждой из этих станций потребность в вагонах соответственно равна 80, 60, 70, 100 и 50. Тарифы перевозок задаются матрицей 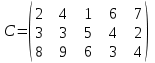 Составить такой план перегонок вагонов, при котором общая стоимость была минимальной. Вариант4 Компания "Royal Wedgetoun Pottery" получила заказы на три вида выпускаемой ею продукции (бокалы, чашки и вазы), которые необходимо удовлетворить в течение следующей недели. Размеры заказов следующие:
В распоряжении компании имеются три станка, на каждом из которых можно производить любой из указанных видов продукции с одинаковой производительностью. Однако единичные затраты по каждому виду продукции варьируют в зависимости от используемого станка. В табл. 8.16 приведены единичные издержки (ф. ст.) по каждому станку. Таблица 8.16
Кроме того, известно, что производственные мощности станков В и С на следующую неделю составят 3000 единиц, а станка А - 2000 единиц. Требуется, используя транспортную модель, найти план производства для видов продукции и станков, минимизирующий общую стоимость производства. Определить значение минимальной стоимости. Если найденное оптимальное решение не единственное, нужно привести другие варианты решений, которым соответствует минимальная стоимость производства. Если бы менеджер по производству захотел, чтобы в производственном плане было как можно меньше изменений в производстве изделий на различных станках, то какое оптимальное решение вы бы порекомендовали? Вариант5 Компания "Orange Computer" производит только один вид продукции - матричные печатающие устройства, которые в настоящее время являются дефицитом. Четыре основных покупателя - это крупные специализированные компьютерные универмаги, расположенные в Аббатстауне, Бесвиче, Карлике и Денстоуне, уже подали заявки, общий размер которых превышает общие производственные мощности трех заводов компании в Рексфорде, Сидоне и Тристроне. Компания должна принять решение о том, как распределить производственные мощности, чтобы получить максимальную прибыль. После того, как каждый принтер тщательно упакован в мягкую упаковку, предохраняющую его от каких-либо повреждений, его помещают в отдельную коробку. В табл.2.17 приведены значения стоимости транспортировки одной единицы от каждого завода-производителя в каждый специализированный универмаг (ф. ст.): Таблица 8.17
Поскольку все четыре специализированных универмага расположены в различных частях страны и, следовательно, стоимость транспортировки продукции между заводами-производителями и универмагами различна, а также ввиду некоторых различий и в издержках производства каждого из четырех заводов, существующая структура цен предусматривает возможность установления различных цен для каждого из четырех универмагов. В настоящее время установлены следующие цены за единицу продукции: 230 ф. ст. в Аббатстауне, 235 ф. ст. в Бесвиче, 225 ф. ст. в Карлике и 240 ф. ст. в Денстоуне. Издержки производства на единицу продукции составляют 150 ф. ст. на заводах в Рексфорде и Тристроне и 155 ф. ст. на заводе в Сидоне. Требуется сформировать матрицу, состоящую из входящих в прибыль единичных доходов, соответствующих каждой паре перевозок с заводов-производителей в универмаги. Значения спроса в Аббатстауне, Бесвиче, Карлике и Денстоуне равны 850, 640, 380 и 230 единицам соответственно. Производственные мощности позволяют производить на заводе в Рексфорде 625, в Сидоне - 825, а в Тристроне - 450 принтеров. Используя алгоритм решения транспортной задачи, определить оптимальное распределение перевозок. Определить соответствующую оптимальному решению прибыль. Вариант 6 Решить транспортную задачу со следующими условиями (табл.8.18). Таблица 8.18
Вариант 7 Решить транспортную задачу. А – вектор мощностей поставщиков, В- вектор мощностей потребителей, С- матрица транспортных издержек на единицу груза: А = (300; 350; 150; 200) В= (400; 400; 200) 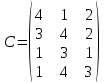 Вариант 8 Решить транспортную задачу. А – вектор мощностей поставщиков, В- вектор мощностей потребителей, С- матрица транспортных издержек на единицу груза: А = (20; 30; 40; 20) В= (40; 40; 20) 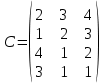 Вариант 9 Решить транспортную задачу со следующими условиями (табл. 8.19). Таблица 8.19
Вариант 10 Решить транспортную задачу со следующими условиями (табл. 8.20). Таблица 8.20
Вариант 11 Решить транспортную задачу со следующими условиями (табл. 8.21). Таблица 8.21
Вариант 12 Решить транспортную задачу со следующими условиями (табл. 8.22). Таблица 8.22
Вариант 13 Решить транспортную задачу со следующими условиями (табл. 8.23). Таблица 8.23
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
