Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы

• Название: Лабораторная работа 1 Решение логических задач Цель работы
• Дата: 06.12.2021
• Размер: 454.13 Kb.
• Имя файла: Лабораторная работа №1 Решение логических задач.docx
• Тип: Лабораторная работа; #293179
• страница: 19 из 21

8.2. Транспортная задача

Контрольный пример

Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл.8.14.

Таблица 8.14

		1	2	3	4	5
		Лос-Анджелес	Даллас	Сен-Луис	Вашингтон	Атланта
1	Денвер	1,50	2,00	1,75	2,25	2,25
2	Бостон	2,50	2,00	1,75	1,00	1,50
3	Новый Орлеан	2,00	1,50	1,50	1,75	1,75
4	Даллас	2,00	0,50	1,75	1,75	1,75

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции. В противном случае в модель нужно было бы ввести:

• 
  в случае перепроизводства - фиктивный пункт распределения, стоимость перевозок единицы продукции в который полагается равной стоимости складирования, а объемы перевозок объемам складирова­ния излишков продукции на фабриках;
  
• 
  в случае дефицита - фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок - объемам недопоставок про­дукции в пункты распределения.
  

Для решения данной задачи построим ее математическую модель: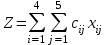



Неизвестными в данной задаче являются объемы перевозок. Пусть x_ij - объем перевозок с i-ой фабрики в j-й центр распределения. Функция цели - это суммарные транспортные расходы, т. е. где с_ij – стоимость перевозки единицы продукции с i-и фабрики j-й центр распределения.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

• 
  Объемы перевозок не могут быть отрицательными.
  
• 
  Так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.
  

В результате имеем следующую модель: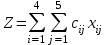

- минимизировать при ограничениях:
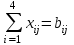, j  [1,5],

x_ij  0, i [1,4], j [1,5],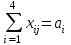

, i [1,4],

где a_ij - объем производства на i-й фабрике, bj - спрос в j-м центре распределения.

Решение задачи с помощью MSExcel.

1. 
   Ввести данные, как показано на рис. 8.6.
   

В ячейки А1:Е4 введены стоимости перевозок. Ячейки А6:Е9 отведены под значения неизвестных (объемы перевозок). В ячейки G6:G9 введены объемы производства на фабриках, а в ячейки А11:Е11 введена потребность в продукции в пунктах распределения. В ячейку F10 введена целевая функция =СУММПРОИЗВ(А1:Е4;А6:Е9).



Рис. 8.6. Исходные данные транспортной задачи

В ячейки А10:Е10 введены формулы

=СУММ(А6:А9)

=СУММ(В6:В9)

=СУММ(С6:С9)

=СУММ(06:О9)

=СУММ(Е6:Е9) определяющие объем продукции, ввозимой в центры распределения.

В ячейки F6:F9 ведены формулы

=СУММ(А6:Е6)

=СУММ(А7:Е7)

=СУММ(А8:Е8)

=СУММ(А9:Е9) вычисляющие объем продукции, вывозимой с фабрик.

2. 
   Выбрать команду Сервис/Поиск решения (Tools/Solver) и заполнить открывшееся диалоговое окно Поиск решения (Solver), как показано на рис.8.7.
   

Внимание! В диалоговом окне Параметры поиска решения (Solver Options) необходимо установить флажок Линейная модель (Assume Linear Model).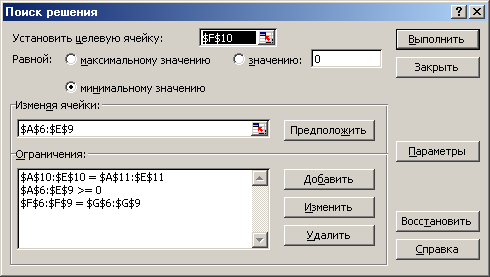


Рис.8.7. Диалоговое окно Поиск решения для транспортной задачи

3. После нажатия кнопки Выполнить (Solve) средство поиска решений находит оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 8.8).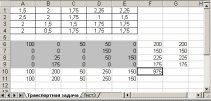


Рис.8.8. Оптимальное решение транспортной задачи

Индивидуальное задание

1. 
   Построить математическую модель задачи, согласно вашему варианту.
   
2. 
   Решить задачу с помощью средства MS Exscel Поиск решения.
   
3. 
   Сделать соответствующие выводы.
   

Вариант 1

Решить транспортную задачу со следующими условиями (табл.8.15):

Таблица 8.15

Пункты отправления	Пункты назначения				Запасы
	В1	В2	В3	В4
А1	3	4	6	1	460
А2	5	1	2	3	340
A3	4	5	8	1	300
Потребности	350	200	450	100