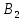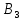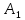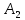Решение матричной игры в чистых и смешанных стратегиях. Лаб №1. Лабораторная работа 1 Решение матричной игры в чистых и смешанных стратегиях
 Скачать 476.33 Kb. Скачать 476.33 Kb.
|
|
Лабораторная работа №1 «Решение матричной игры в чистых и смешанных стратегиях». Цель лабораторной работы - научиться находить нижнюю и верхнюю цену игры и решать ее в чистых и смешанных стратегиях, используя электронные таблицы. Задание на лабораторную работу У стороны А имеются две стратегии развития фирмы ( 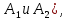 у стороны В – три( у стороны В – три(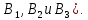 Известны вероятностные выигрыши сторон при использовании ими той или иной стратегии. Платежная матрица имеет вид: Известны вероятностные выигрыши сторон при использовании ими той или иной стратегии. Платежная матрица имеет вид: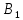 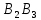 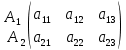 Используя данные индивидуального задания, найти верхнюю и нижнюю цену игры и сделать вывод об отсутствии седловой точки. Исключить доминируемую стратегию (предполагается, что она есть). Найти решение игры в смешанных стратегиях, выполнив расчеты в среде электронных таблиц. Вариант индивидуального задания:
1.Решение игры в чистых стратегиях Для нахождения оптимальной стратегии необходимо последовательно проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Минимальные числа в каждой строке обозначим 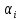 и выпишем в виде добавочного столбца платежной матрицы: и выпишем в виде добавочного столбца платежной матрицы: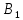 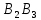 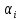 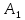 40 70 50 40 40 70 50 40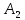 70 35 30 30 70 35 30 30Предпочтительной для игрока А будет та стратегия, при которой 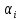 обращается в максимум, т.е. обращается в максимум, т.е. 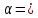 min min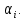 Нижняя цена игры — это тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии. 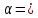 maxminqij, maxminqij,α = 40 Аналогичные рассуждения проводим и для стороны игрока В. Эта сторона должна рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения выигрыша: 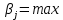 qij. qij.Эти значения выписываем в дополнительной строке платежной матрицы. Из всех значений 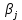 находим минимальное. находим минимальное.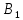 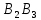 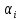 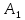 40 70 50 40 40 70 50 40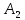 70 35 30 30 70 35 30 30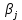 70 70 50 70 70 50β = min 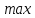 qij. qij.β = 50 – верхняя цена игры. Так как не выполняется равенство maxminqij = min 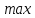 qij, qij, 40<50 платежная матрица не имеет седловой точки, задача решений в чистом виде не имеет. 2. Решение игры в смешанных стратегиях Стратегия, состоящая в случайном применении с определенными вероятностями тех или иных чистых стратегий, называется смешанной стратегией. Простейшая матричная игра 2х2 определяется матрицей A = 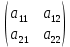 , ,Уменьшим порядок платёжной матрицы (количество строк и столбцов) за счёт исключения доминируемых и дублирующих стратегий. Рассмотрим платежную матрицу выигрышей, показанную в таблице 2.1. Таблица 2.1 — Платёжная матрица с доминируемыми стратегиями
Доминируемая стратегия для игрока A, когда все элементы строки матрицы этой стратегии меньше или равны соответствующим элементам строки матрицы другой стратегии. В нашем случае стратегия A2 является доминируемой по отношению к стратегии A1, и ее можно исключить из рассмотрения. Найдем оптимальную смешанную стратегию, выполнив расчеты в среде Excel. Заносим на лист Excel исходные данные (платежную матрицу) и проверяем их на наличие седловой точки. Вид листа Excel показан на рисунке 2.1. 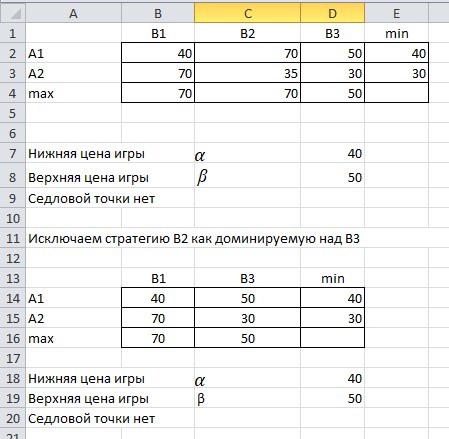 Рисунок 2.1 - Вид листа Excel не имеющей седловой точки Находим доминируемую стратегию для игрока B, когда все элементы столбца матрицы этой стратегии больше или равны соответствующим элементам столбца матрицы другой стратегии. В нашем случае стратегия B2 является доминируемой по отношению к стратегии B3 и ее можно исключить из рассмотрения. Вид листа Excel исключающую стратегию В2 показан на рисунке 2.2. 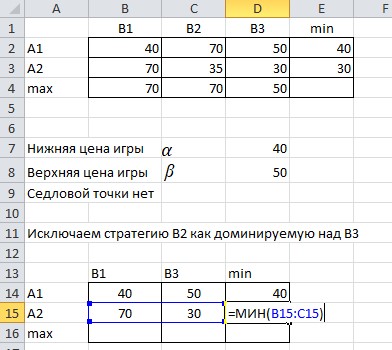 Рис.2.2 - Вид листа Excel исключающую стратегию В2 Находим min 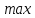 qijи maxminqij,определяем нижнюю и верхнюю цену игры. Определяем вероятности чистых стратегий в смешанной. Вводим соответствующие формулы для организации вычислений. Вид листа Excel для поиска нижней и верхней цены игры показан на рисунке 2.3. qijи maxminqij,определяем нижнюю и верхнюю цену игры. Определяем вероятности чистых стратегий в смешанной. Вводим соответствующие формулы для организации вычислений. Вид листа Excel для поиска нижней и верхней цены игры показан на рисунке 2.3.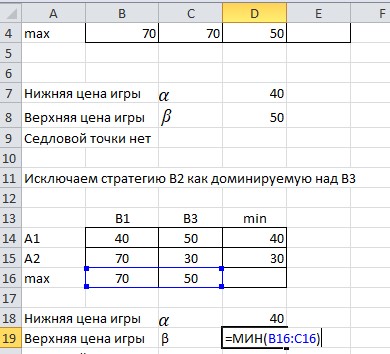 Рисунок 2.3 - Вид листа Excel для поиска нижней и верхней цены игры Определяем вероятности чистых стратегий в смешанной. Вид листа Excel для поиска вероятности чистых стратегий в смешанной показан на рисунке 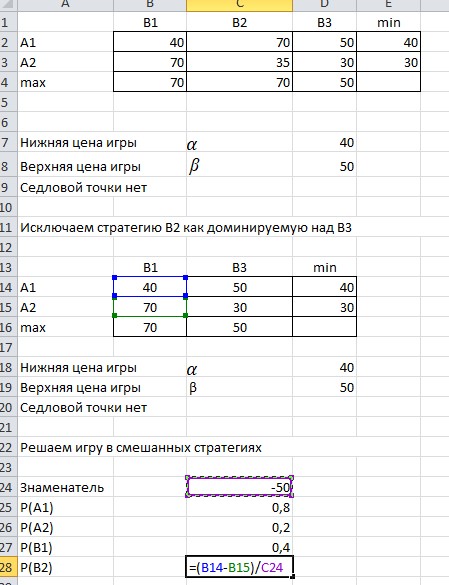 Рисунок 2.4 - Вид листа Excel для поиска вероятности чистых стратегий в смешанной Находим чистую цену игры для игрока А. Вид листа Excel для поиска чистой цены игры для игрока А показан на рисунке 2.5. 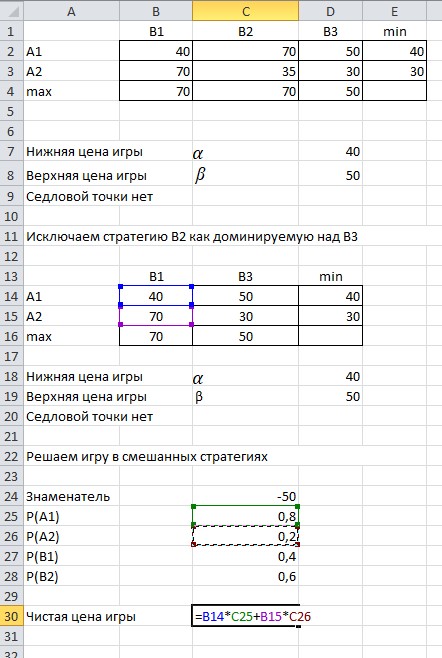 Рисунок 2.5 - Вид листа Excel для поиска чистой цены игры для игрока А Находим чистую цену игры для игрока В. Вид листа Excel для поиска чистой цены игры для игрока В показан на рисунке 2.6. 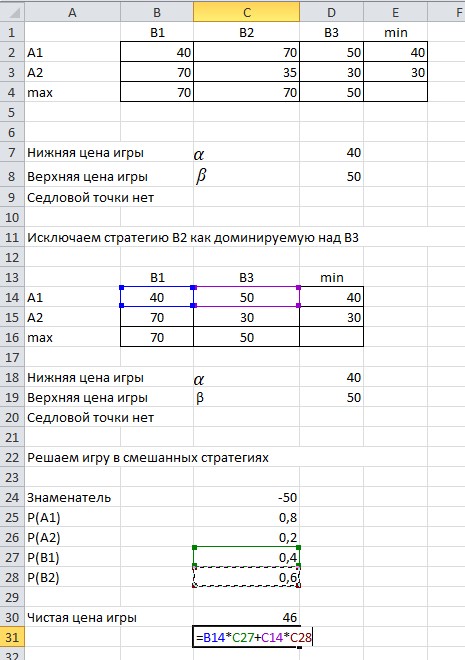 Рисунок 2.6 - Вид листа Excel для поиска чистой цены игры для игрока В Вид листа Excel для поиска оптимальной смешанной стратегии показан на рисунке 2.7. 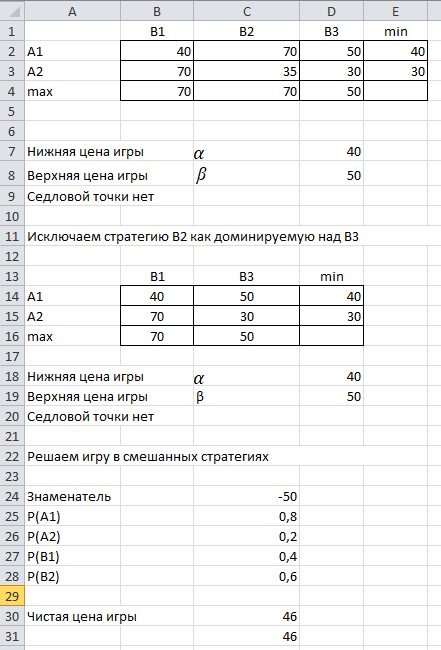 Рисунок 2.7 – Вид листа Excel для поиска оптимальной смешанной стратегии В результате получены следующие значения вероятностей чистых стратегий в смешанной: P(A1)=0,8; P(A2)=0,2; P(B1)=0,4; P(B2)=0,6 Это означает, что предприятию A следует производить 80% первого вида продукции и 20% второго вида, а предприятию B — соответственно 40% и 60%. При этом чистая цена игры составит 46 д.е. Вывод: мы научились находить нижнюю и верхнюю цену игры и решать ее в чистых и смешанных стратегиях, используя электронные таблицы. |