Лабораторная работа 1. студент группы ивт4116 Лукина Елизавета Витальевна Проверил Первова Н. В

• Название: Лабораторная работа 1. студент группы ивт4116 Лукина Елизавета Витальевна Проверил Первова Н. В
• Дата: 13.10.2018
• Размер: 249.74 Kb.
• Имя файла: otchetvichmat1lr.docx
• Тип: Лабораторная работа; #53253

ФГБОУ ВПО Чувашский государственный университет имени И.Н.Ульянова
Факультет Информатики и вычислительной техники

Кафедра вычислительной техники

Лабораторная работа №1.

Выполнил: студент группы ИВТ-41-16 Лукина Елизавета Витальевна Проверил: Первова Н.В.

Чебоксары 2018

ЗАДАНИЕ:

1. Построить график функции y=f(x) на отрезке [x0, x1].

2. Найти корень заданного уравнения f(x)=0 с заданной точностью ε на заданном

отрезке [x0, x1].

3. Привести расчёты параметров итерационного процесса для каждого шага

алгоритма.

4. Решить исходное уравнение с помощью встроенной функции roots, fzero, sqp.

5. Сравнить результаты, полученные в п.2 и 4.

6. Записать в ответе только верные цифры.

УРАВНЕНИЕ f(x)=0 И НАЧАЛЬНЫЕ ДАННЫЕ:

x0= –0.7, x1= 1.5, ε= 0.01

МЕТОД РАССЧЁТА:

Метод секущих.
Алгоритм метода решения нелинейного уравнения
Решение нелинейных уравнений состоит из 2-ух этапов:

1. 
   Отделение корней
   
2. 
   Уточнение корней
   

График заданной функции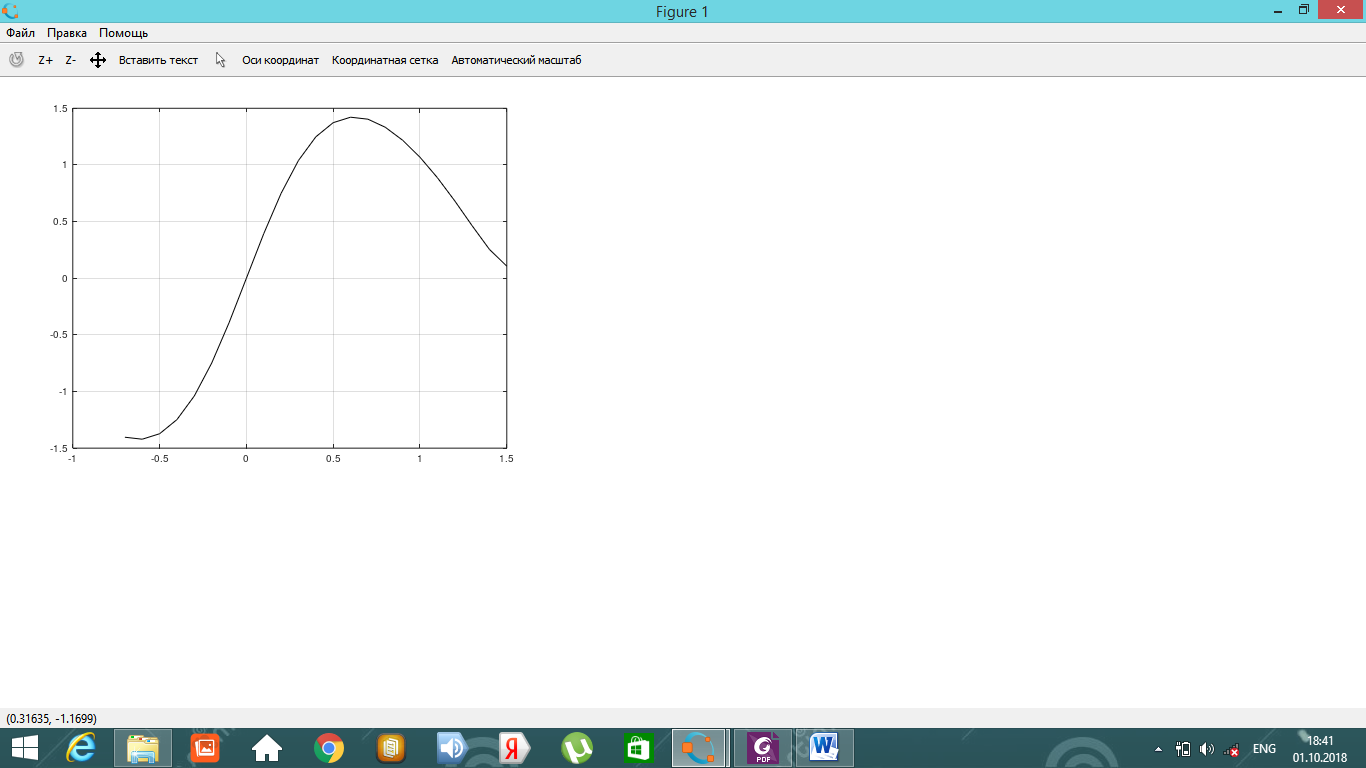



Значения параметров итерационного процесса для каждого шага алгоритма

№	a	b	c	F(a)	F(b)	F(c)	|F(c)|<0,01
1	-0.20000	0.047173	0.047173	-0.74947	0.18800	0.18800	Нет
2	-0.0023942	0.047173	-0.0023942	-0.0095769	0.18800	-0.0095769	Да

x0= -0.00000000019191


Визуализацию последнего шага алгоритма с выводом всех промежуточных вспомогательных прямых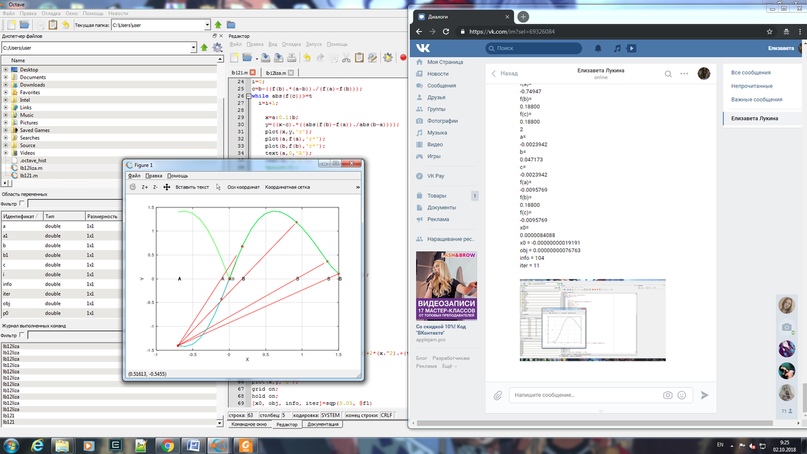



Решения исходного уравнения с помощью встроенных функций roots, fzero, sqp.

Функция [x, obj, info, iter] = sqp(x0, phi, g, h, lb, ub,maxiter, tolerance) предназначена для решения следующей оптимизационной задачи: найти минимум функции ϕ(x) при следующих ограничениях g(x) = 0, h(x) ≥ 0, lb ≤ x ≤ ub. Функция sqp при решении задачи оптимизации использует метод квадратичного программирования.


[x0, obj, info, iter]=sqp(0.05, @f)

x0 = -0.00000000019191 
obj = 0.00000000076763 

info = 104 
iter = 11

Анализ результатов решения уравнения и выводы по работе

Нахождение корня уравнения методом секущих оказался быстрее (2 итерации), чем нахождение корня с помощью встроенной функции sqp (11 итераций).
Текст программы

a=-0.7; 
a1=a; 
b=1.5; 
b1=b; 
t=0.001; 
function y=f(x) 
y=((x.^3))/50+(8*sin(x)./(2+2*(x.^2).+(tan(x).*tan(x)))); 
end; 
if a>b 
c=a; 
a=b; 
b=c; 
end; 
x=a1:0.1:b1; 
y=f(x); 
plot(x,y,'k'); 
grid on; 
hold on; 
xlabel('X'); 
ylabel('Y'); 
text(a,0,'A'); 
text(b,0,'B'); 
pause(5); 
i=0; 
a=a+0.5; 
b=b-1; 
c=a-((f(a).*(b-a))./(f(b)-f(a))); 
while abs(f(c))>=t 
i=i+1; 
x=a:0.1:b; 
y=((x-c).*((abs(f(b)-f(a))./abs(b-a)))); 
plot(x,y,'r'); 
plot(a,f(a),'r*'); 
plot(b,f(b),'r*'); 
text(a,0,'P0'); 
text(b,0,'P1'); 
pause(5); 
hold on; 
if f(b)*f(c)<0 
a=c; 
else 
b=c; 
end; 
disp(i); 
disp('a='); disp(a); 
disp('b='); disp(b); 
disp('c='); disp(c); 
disp('f(a)='); disp(f(a)); 
disp('f(b)='); disp(f(b)); 
disp('f(c)='); disp(f(c)); 
c=a-((f(a).*(b-a))./(f(b)-f(a))); 
end; 
x=a1:0.1:b1; 
y=f(x); 

plot(x,y,'c'); 
grid on; 
hold on; 
plot(c,0,'r*'); 
xlabel('X'); 
ylabel('Y'); 
text(a1,0,'A'); 
text(b1,0,'B'); 
text(c,f(c),'X0'); 
disp('x0=');disp(c); 
function y1=f1(x) 
y1=abs(((x.^3))/50+(8*sin(x)./(2+2*(x.^2).+(tan(x).*tan(x))))); 
end; 
pause(5); 
y=f1(x); 
plot(x,y,'b'); 
grid on; 
hold on; 
[x0, obj, info, iter]=sqp(0.05, @f1)