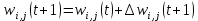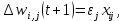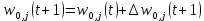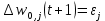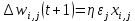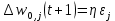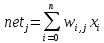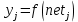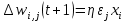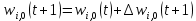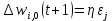Обучение однослойного персептрона методом коррекции по ошибке через дельта-правило. Лабораторная работа № 1. Образец оформления. Лабораторная работа 1 Вариант 1 магистрант гр. 2Миб1501 Иванов И. И. подпись дата Проверил
 Скачать 33.13 Kb. Скачать 33.13 Kb.
|
|
Ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования Московский технический университет связи и информатики Факультет повышения квалификации Лабораторная работа №1 Вариант 1 Выполнил: магистрант гр. 2МИБ1501 Иванов И.И. ________________________ подпись дата Проверил: к.т.н. Махров С.С. ________________________ подпись дата Москва 2016 Обучение однослойного персептрона методом коррекции по ошибке через дельта-правило Цель работы. Изучить алгоритм обучения однослойного персептрона методом коррекции по ошибке через дельта-правило. Задание. В соответствии с вариантом, необходимо обучить нейронную сеть распознавать указанные 4 символа. На каждый символ необходимо подготовить 4 обучающих образа с использованием разных шрифтов. Соответственно, всего будет 16 обучающих образов: 4 образа первым шрифтом, 4 образа, вторым шрифтом и т.д. Тестовая выборка должна содержать по 1 образу на каждый из 4-х символов. Символы должны быть написаны другим шрифтом, который не был использован в обучающей выборке. Теоретические сведения. Алгоритм обучения с положительным и отрицательным подкреплением можно представить в более общей форме – в виде дельта-правила. Если за dj обозначить желаемый выходной сигнал j-го нейрона (от слов desire response, что в переводе с английского означает «желаемый отклик»), то на каждой эпохе (итерации) обучения можно рассчитывать разницу между желаемым dj ответом j-го нейрона и реальным значением yj, вычисляемым на его выходе. Соответственно, ошибкой выхода персептрона называется следующее выражение: 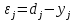 Тогда относительно алгоритма обучения персептрона с положительным и отрицательным подкреплением: - случай εj = 0 соответствует шагу 4а; - случай εj > 0 соответствует шагу 4б; - случай εj < 0 соответствует шагу 4в. Идея алгоритма обучения персептронного слоя с помощью правила Хебба сохранится, если итерационный процесс корректировки весов вести по формулам:
где wi,j(t) и wi,j(t+1) – старое и новое значения синаптических весов персептрона, Δwi,j(t + 1) – новое значение величины коррекции синаптических весов персептрона, i – номер входного сигнала, j – номер нейрона. Приведенные формулы называются дельта-правилом. Кроме того, можно получить аналогичную итерационную формулу для подстройки нейронного смещения b, если учесть, что его можно интерпретировать как вес w0,j дополнительного входа x0,j, значение которого всегда равно 1:
В итерационные формулы полезно ввести коэффициент скорости обучения η, с помощью которого можно управлять величиной коррекции синаптических весов и нейронного смещения:
При слишком больших значениях коэффициента η обычно теряется устойчивость процесса обучения, тогда как при слишком малых – увеличивается время обучения. На практике коэффициент скорости обучения η обычно задают в пределах от 0.05 до 1. Алгоритм обучения персептрона с использованием этих формул известен под названием обучения с коррекцией по ошибке или дельта-правило. В общем виде, алгоритм обучения с коррекцией по ошибке через дельта-правило, представлен ниже. Алгоритм обучения методом коррекции по ошибке через дельта-правило Шаг 1. Подготовить обучающую выборку, каждый элемент которой будет состоять из пар (X, D)m (m=1,…q) – обучающего вектора X = (x1,…,xn) (i=1,…,n) с вектором желаемых значений D = (d1,…,dk) (j=1,…,k) выходов персептрона. Шаг 2. Генератором случайных чисел всем синаптическим весам wij и нейронным смещениям w0,j (i=1,…,n; j=1,…,k) присваиваются некоторые малые случайные значения. Шаг 3. Из обучающей выборки (X, D)1,…,(X, D)q, взять следующий по счету вектор Xт = (x1,…,xn) и подать его на входы персептрона x1,…,xn. Сигналам нейронных входов смещения x0 присваиваются единичные значения: x0 = 1. Шаг 4. Для каждого j-го нейрона вычислить взвешенную сумму входных сигналов netj и выходной сигнал yj на основании функции активации f:
Шаг 5. Для каждого j-го нейрона вычислить его ошибку: 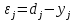 где dj – вектор правильных (желаемых) ответов персептрона. Шаг 6. Произвести коррекцию синаптических весов j-го нейрона и нейронных смещений:
где t – номер итерации. Шаги 4-6 повторяются для всех нейронов персептронного слоя при подаче конкретного образа. Шаги 3-6 выполняются последовательно для каждого входного образа, на котором обучается персептрон. Шаг 7. После подачи последнего обучающего вектора, проверить критерий останова обучения, если он выполняется, то завершить обучение. В противном случае – возврат к шагу 3. Критерии останова алгоритма обучения могут быть следующими: Значения синаптических весов wi,j перестают изменяться; Перестают появляться неправильные выходные сигналы yj; Превышен установленный лимит количества эпох (либо итераций). Указанные критерии останова обучения используются как по отдельности, так и вместе. Важным замечанием будет то, что 3-ий критерий, при задании недостаточного количества эпох, может привести к недообучению сети, поэтому его использование в промышленном применении не рекомендуется, но в учебных целях он показателен и удобен. Ход выполнения работы (Ход выполнения работы должен быть описан достаточно подробно со скриншотами нарисованных образов, указанием параметров, при которых обучалась сеть (скорость обучения, какой критерий останова использовался, диапазон, из которого случайным образом назначались значения синаптических весов при старте сети). Вывод. (Сделать вывод об ассоциативных свойствах однослойного персептрона, указать наблюдения, полученные в результате обучения через дельта-правило. Везде ли были корректные ответы? Если нет, указать почему? Если ответы некорректные, то можно попробовать задать более низкую скорость обучения, увеличить количество эпох, генерировать при старте нейронной сети синаптические веса не из дипазона [-0.03, 0.03], а из [-0.003, 0.003] или [-0.0003, 0.0003] и т.д.) Исходный код программы (Привести исходный код каждого java-класса) |