Лабораторная работа №10. Лабораторная работа 10 определение отношения теплоемкости воздуха при постоянном давлении и постоянном объеме цель лабораторной работы
 Скачать 37.1 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 10 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ПОСТОЯННОМ ОБЪЕМЕ Цель лабораторной работы: ознакомление с одним из методов определения отношения теплоемкости воздуха при постоянном давлении Сp к теплоемкости воздуха при постоянном объеме Сv. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ Способность любого тела изменять свою температуру при сообщении ему теплоты характеризуется теплоемкостью тела. Применительно к газам наиболее часто используется понятие молярной теплоемкости. Молярная теплоемкость газа – это величина, численно равная количеству теплоты, необходимому для нагревания 1 моля газа на 1 К 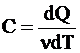 ,  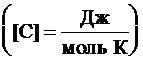.Из первого начала термодинамики вытекает, что теплоемкость газов зависит от условий нагревания, т. е. теплоемкость будет различной, если нагревать газ при постоянном объеме (Сv) или при постоянном давлении (Cp). Действительно, если газ расширяется изобарически (при P = const ), то согласно первому началу термодинамики Q = DU + A, (1) количество теплоты Q, полученное газом, расходуется на изменение его внутренней энергии U (U – суммарная, механическая энергия всех молекул газа, [U] = Дж) и на совершение работы А ([А] = Дж). Если же процесс изохорический (при V = const ), то работа А = 0 и первый закон термодинамики примет вид: Q = DU, (2) т. е. тепло расходуется лишь на изменение внутренней энергии газа. Если в обоих случаях температура изменилась на 1 К, то изменение внутренней энергии одинаково и из сравнения (1) и (2) очевидно, что при изобарическом процессе теплоемкость больше на величину совершенной работы А, т. е. Сp > Cv. Для определения отношения теплоемкости при постоянном давлении Сp к теплоемкости при постоянном объеме Cv следует рассмотреть процесс, где это отношение играет существенную роль. Таким процессом является адиабатический процесс – процесс, происходящий при отсутствии теплообмена газа с окружающей средой. Адиабатический процесс описывается уравнением Пуассона:  , (3)либо  . (4)Здесь Р – давление газа ([Р] = Па), V - объем газа ([V] = м3) и 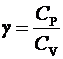 (5) – показатель адиабаты. 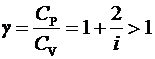Для идеального газа показатель адиабаты будет равен , (6)здесь i – количество степеней свободы молекулы рассматриваемого газа, т. е. число координат, необходимое и достаточное для описания положения молекулы в пространстве. Из выражения (6) видно, что для определения отношения теплоемкостей необходимо вычислить g. В реальных условиях добиться адиабатического процесса, т. е. осуществить полную теплоизоляцию, очень трудно. На практике пользуются тем фактом, что установление равновесного давления протекает очень быстро – за доли секунды, а на выравнивание температуры вследствие теплообмена газа с внешней средой требуются минуты. Следовательно, для осуществления процесса, близкого к адиабатическому, достаточно быстро изменить давление в газе. СХЕМАТИЧЕСКОЕ ИЗОБРАЖЕНИЕ УСТАНОВКИ 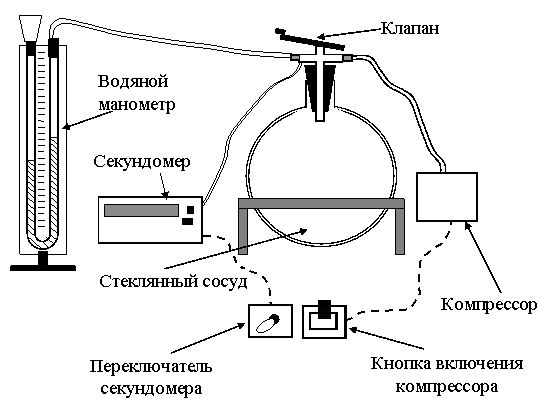 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Задание 1 Форула для нахождения γ 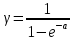 Формула для нахождения среднего арифметического значения γср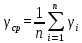 
Все измеренные и посчитанные величины представлены в таблице 1 Таблица 1 РАСЧЕТ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ Вывод: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||