ФИЗИКА ЛАБОР.. Лабораторная работа 11 Дайте определение основных кинематических величин, характеризующих вращательное движение твёрдого тела
 Скачать 175 Kb.
|
|
Лабораторная работа № 11 1. Дайте определение основных кинематических величин, характеризующих вращательное движение твёрдого тела. Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:  ,а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени. Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью  определяется формулой: где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.Ине́рция (от лат. inertia — бездеятельность, косность) — явление сохранения скорости тела в случае, если внешние воздействия на него отсутствуют или взаимно скомпенсированы. Существование явления инерции в классической механике постулируется Первым законом Нью́тона, который также называется Зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.» Современная формулировка закона: «Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.» Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными. Проявлением неинерциальности в них является возникновение фиктивных сил, называемых «силами инерции». 2. Связь линейных и угловых параметров вращательного движения. Отдельные точки вращающегося тела имеют различные линейные скорости  . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости  определяется скоростью вращения тела  и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени  тело повернулось на угол  (рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный Линейная скорость точки по определению.
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:  подставляя значение скорости из (2.6), находим:
Тангенциальное ускорение 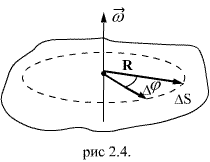  Воспользовавшись тем же отношением (2.6) получаем
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения. 3. Что называют моментом силы, моментом импульса, моментом инерции? В каких единицах они измеряются? Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, т.к в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). Момент силы  Размерность - L2MT−2 Единицы измерения: СИ - Ньютон-метр Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно - если в задаче есть центральная или осевая симметрия, но не только в этих случаях). Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр. Момент импульса замкнутой системы сохраняется. Момент импульса  Размерность - L2MT−1 Единицы измерения: СИ - м2·кг·с−1 СГС - см2·г·с−1 Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. Момент инерции  Размерность - L2M Единицы измерения: СИ - кг·м² СГС - г·cм² 4. Вывести основное уравнение динамики вращательного движения. Согласно уравнению (  ) второй закон Ньютона для вращательного движенияПо определению угловое ускорение  и тогда это уравнение можнопереписать следующим образом  с учетом (5.9)  или
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела  , равно импульсу момента  всех внешних сил, действующих на это тело.5. Сформулируйте теорему Гюйгенса-Штейнера. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела Ic относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: Inew = Ic + md2, где m — масса тела, d — расстояние между осями. Например, Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью C) равен  Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен J = JC + md2, где d — расстояние между искомой осью и осью C. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле d = L / 2:  Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор  относительно произвольной точки из тензора  относительно центра масс. Пусть  — смещение от центра масс, тогда где  — вектор смещения от центра масс, а δij — символ Кронекера.Как видно, для диагональных элементов тензора (при i = j) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси. Иллюстрация теоремы для момента площади. 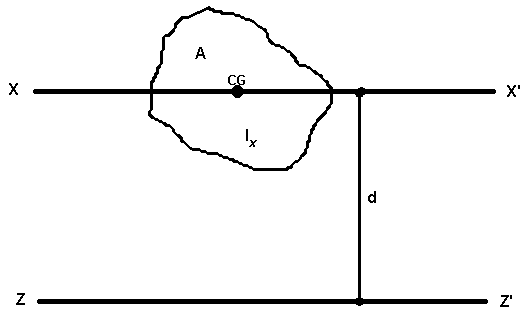 6. В чём состоит суть метода определения момента инерции на трифилярном подвесе. . 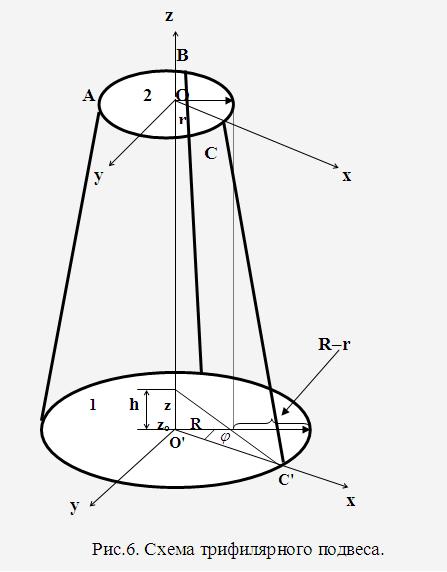 Одним из методов определения моментов инерции твердых тел, является метод крутильных колебаний, осуществляемый с помощью трифилярного подвеса (Рис.6), который состоит из платформы 1, подвешенной на трех симметрично закрепленных нитях к неподвижно закрепленному диску 2 меньшего диаметра. Центры масс диска 2 и платформы 1 находятся на одной оси ОО', относительно которой платформе можно сообщить крутильные колебания, при этом центр тяжести платформы точки О' перемещается по этой оси. (ОСТАЛЬНОЕ В ОТДЕЛЬНОМ ДОКУМЕНТЕ!!) Лабораторная работа № 2 1. Колебания. Гармонические колебания. Уравнения гармонических колебаний. Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:  или  ,где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний,  — полная фаза колебаний,  — начальная фаза колебаний.Обобщенное гармоническое колебание в дифференциальном виде  Любое нетривиальное решение этого дифференциального уравнение - есть гармоническое колебание с циклической частотой ω. 2. Параметры гармонических колебаний. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Циклическая частота колебаний - связана с частотой колебаний соотношением  . Единица циклической частоты — радиан в секунду (рад/с, rad/s). В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно). 3. Маятник математический (теория). Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести. 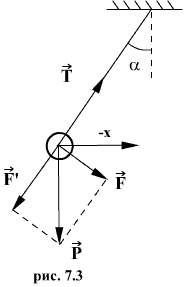 Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая  , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения  и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α  Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения Момент силы относительно точки О:  , и момент инерции:M = FL . Момент инерции J в данном случае Угловое ускорение:  С учетом этих величин имеем:  или
Его решение  ,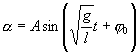
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний. 4. Виды колебаний (свободные, затухающие, вынужденные), примеры. Свободные (или собственные) колебания — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебания являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида  в природе невозможен.Вынужденныеколебания — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия. 5. Физический маятник (теория). Ф 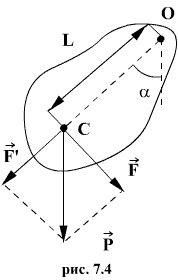 изическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F. Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения  . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
Решение этого уравнения 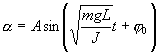 Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.  или .Из этого соотношения определяем  Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника. |
и 
