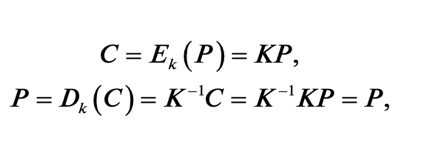Лабораторная работа №13. ШИФРЫ МНОГОБУКВЕННОЙ ЗАМЕНЫ НА ПРИМЕРЕ ШИФРА ХИЛЛА
Цельработы:Выполнить шифрование и дешифрование сообщений.
Описание объекта исследования
Одним из интересных представителей многобуквенных шифров является шифр, разработанный математиком Лестером Хиллом в 1929 году. Лежащий в его основе алгоритм заменяет каждые тпоследовательных букв откры- того текста тбуквами шифрованного текста. Подстановка определяется тлинейными уравнениями, в которых каждому символу присваивается числовое значение (a = 0, b = 1, c = 2, …, z = 25). Например, при т= 3, получаем следующую систему уравнений:
С1 = (k11 p1 + k12 p2 + k13 p3 )mod 26 С2 = (k21 p1 + k22 p2 + k23 p3 )mod 26 C3 = (k31 p1 + k32 p2 + k33 p3 )mod 26
Эту систему уравнений можно записать в виде произведения вектора и матрицы в следующем виде:
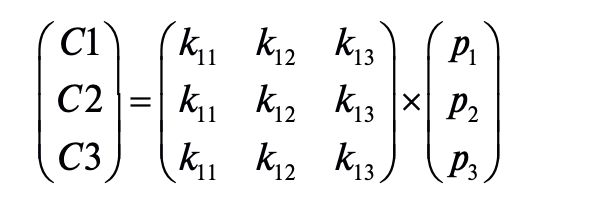 или в виде:
C = KP, где С – вектор длины 3, представляющий шифрованный текст; Р – вектор длины 3, представляющий открытый текст; К – матрица размерности 3×3, представляющая ключ шифрования. Все операции выполняются по модулю 26. Рассмотрим пример шифрования и дешифрования. Пусть матрица К: æ17 17 5 ö  ç ÷
K= ç 21 18 21 ÷ 
è ø
ç 2 2 19 ÷ Первые три буквы открытого текста представлены вектором (15 0 24), таким образом, К(15 0 24) = (275 819 486) mod 26 = (11 13 18) = LNS.
Продолжая вычисления, получим для данного примера шифрованный текст вида: LNSHDLEWTRW.
Для расшифровки необходимо воспользоваться матрицей, обратной К.Обратной по отношению к матрице Кназывается такая матрица K-1,для которой выполняется равенство KK-1 = K-1К=I,где I– это единичная матрица (матрица, состоящая из нулей всюду, за исключением главной диагонали, про- ходящей с левого верхнего угла в правый нижний, на которой предполагаются единицы). Обратная матрица существует не для всякой матрицы, однако когда обратная матрица имеется, для нее обязательно выполняется приведенное выше равенство. В данном примере обратной матрицей является следующая:
æ 4 9 15ö

ç ÷
K-1 = ç 15 17 6 ÷

è ø
ç 24 0 17 ÷
Это проверяется следующими вычислениями:
æ17 17 5 ö æ 4 9 15 ö æ 443 442 442 ö æ 1 0 0 ö

ç ÷ ç ÷ ç ÷ ç ÷
ç 21 18 21÷ ´ç 15 17 6 ÷ = ç 858 495 780 ÷mod 26 = ç 0 1 0 ÷

è ø è ø è ø è ø
ç 2 2 19 ÷ ç 24 0 17 ÷ ç 494 52 365 ÷ ç 0 0 1 ÷
В результате применения матрицы К-1 к шифрованному тексту полу- чается открытый текст. В общем виде криптосистема Хилла записывается соотношением:
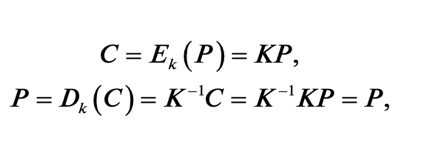 (4.1) где С– шифрованный текст; Р– открытый текст; К– ключ шифрования; Еk– функция шифрования; Dk– функция дешифрования. Преимущество шифра Хилла состоит в том, что он полностью маски- рует частоту вхождения отдельных букв – чем больше размер матрицы, тем больше шифрованном тексте скрывается информации о различиях в значениях частоты появления других комбинаций символов. Так, шифр Хилла с матрицей 3×3 скрывает частоту появления не только отдельных букв, но и двухбуквенных комбинаций. Хотя шифр Хилла устойчив к попыткам криптоанализа в тех случаях, когда известен только шифрованный текст, этот шифр легко раскрыть при наличии известного открытого текста. Рассмотрим шифр Хилла с матрицей т× т. Предположим, что нам известно т пар отрывков открытого и соот- ветствующего шифрованного текстов, каждый длины т. Обозначим такие пары Pj=( p1j, p2j,…, pmj) и Cj=( C1j, C2j,…, Cmj), чтобы выполнялось условие
Cj= KPjдля всех 1 ≤ j ≤ т и некоторой неизвестной ключевой матрицы К.Теперь определим две такие матрицы Х=(рij) и Y= (Сij) размера т×т, что Y=XK.Тогда, при условии что для матрицы Xсуществует обратная матрица, К можно определить по формуле K = X-1К. Если же получить матрицу, обрат- ную матрице Xневозможно, то необходимо сформировать другую матрицу X с дополнительными парами соответствия открытого и шифрованного текстов, до тех пор, пока не будет найдена обратная матрица.
Рассмотрим пример. Предположим, что открытый текст «friday» шифро- ван с помощью шифра Хилла с использованием матрицы 2×2, в результате чего получен шифрованный текст PQCFKU. Таким образом, известно, что K(5 17) = (15 16), K(8 3) = (2 5) и K(0 24) = (10 20). Используя первые две пары символов открытого и шифрованного текстов, получаем:

Порядок выполнения работы
С помощью любого математического пакета сформируйте матрицу-ключ, у которой имеется обратная ей матрица.
Зашифруйте открытый текст.
Передайте зашифрованное сообщение вместе с ключом по локальной сети лаборатории адресату и получите переданное Вам шифрованное сообщение с ключом
Вычислить матрицу обратную полученной в качестве ключа к получен- ному сообщению.
Дешифровать полученное сообщение.
Контрольные вопросы
Предположим, что шифр Хилла используется для зашифрования от- крытого текста, представленного в виде двоичной последовательности. Сколько ключей имеет такой шифр?
К какому виду шифров относится шифр Хилла: поточным или блочным, докажите правильность своих рассуждений.
Приведите сравнительный анализ шифра Хилла и шифра Плейфейера.
Дайте математическое определение обратной матрицы.
Что такое стойкость шифра?
Оцените стойкость шифра Хилла при наличии достаточного числа пар соответствия открытого и шифрованного текстов.
Дайте характеристику шифру Хилла.
В каких современных шифрах применяются идеи, подобные шифру Хилла?
Перечислите недостатки шифра Хилла.
Литература
Столингс В. Криптография и защита сетей. Принципы и практика. 2-е изд. – М.: Вильямс, 2001.
Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы крипто- графии. Учеб. пособие. – М.: Гелиос-АРВ, 2001
|
 Скачать 141.67 Kb.
Скачать 141.67 Kb.