Контрольная по математике. Математика. Задание 1 САB CAB CA
 Скачать 69.15 Kb. Скачать 69.15 Kb.
|
|
Содержание Задание 1…………………………………………………………………………..3 Задание 2…………………………………………………………………………..8 Задание 3…………………………………………………………………………13 Задание 4…………………………………………………………………………14 Задание 1 С=А+B; C=A*B; C=A4; C=3A-2B; C=A+BT А = 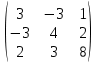 В = В =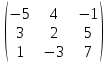 C=A+B = 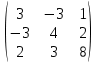 + + 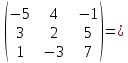 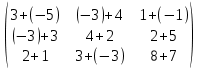 = = 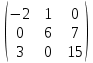 C=A*B = 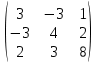 * * 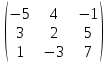 = = 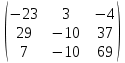 c11=3*(-5)+(-3)*3+1*1=-15-9-1=-23 c12=3*4+(-3)*2+1*(-3)=12-6-3=3 c13=3*(-1)+3*5+1*7=-3-15+7=11 c21=(-3)*(-5)+4*3+2*1=15+12+2=29 c22=(-3)*4+4*2+2*(-3)=(-12)+8-6=-10 c23=(-3)*(-1)+4*5+2*7=3+20+14=37 c31=2*(-5)+3*3+8*1=-10+9+8=7 c32=2*4+3*2+8*(-3)=8+6-24=-10 c33=2*(-1)+3*5+8*7=(-2)+15+56=69 C=A4 = 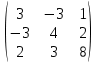 4 = 4 = 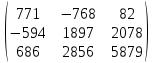 A2 = A*A = 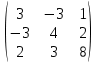 * * 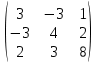 = = 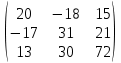 A3 = A*A2 = 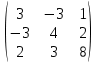 * * 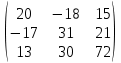 = = 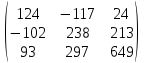 A4 = A * A3 = 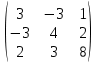 * * 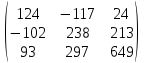 = = 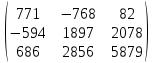 C = 3A-2B = 3 * 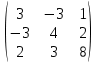 – 2 * – 2 * 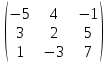 = = 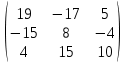 3A = 3 * 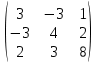 = = 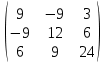 2B = 2 * 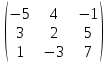 = = 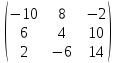 3A-2B = 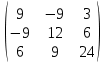 - - 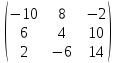 = = 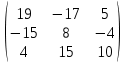 C=A+BT = 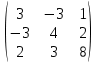 + + 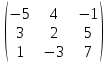 T = T = 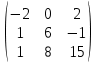 Транспонируем матрицу D=BT = 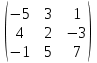 A+D= 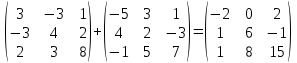 Найти определитель матрицы А = 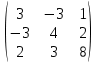 = 3*4*8+(-3)*2*2+1*(-3)*3-1*4*2-3*2*3-(-3)*(-3)*8=96-12-9-8-18-72=-23 = 3*4*8+(-3)*2*2+1*(-3)*3-1*4*2-3*2*3-(-3)*(-3)*8=96-12-9-8-18-72=-23В = 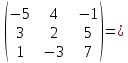 В = В =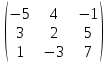 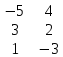 = (-5)*2*7+4*5*1+(- = (-5)*2*7+4*5*1+(-1)*3*(-3)-(-1)*2*1-(-5)*5*(-3)-4*3*7=-198 Найти алгебраические дополнения матрицы А А = 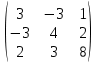 Найдем детерминант матрицы А Det A = 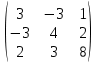 = 3*4*8+(-3)*2*2+1*(-3)*3-1*4*2-3*2*3-(-3)*(- = 3*4*8+(-3)*2*2+1*(-3)*3-1*4*2-3*2*3-(-3)*(-3)*8=96-12-9-8-18-72=-23 Определитель матрицы А отличен от нуля, значит обратная матрица A-1 существует. Найдем дополнительные миноры и алгебраические дополнения матрицы А для вычисления обратной матрицы. M11 = 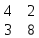 = 4·8 - 3·2 = 32 - 6 = 26 = 4·8 - 3·2 = 32 - 6 = 26А11=(-1)1+1*М11=26 M12 = 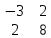 = (-3)·8 - 2·2 = -24 - 4 = -28 = (-3)·8 - 2·2 = -24 - 4 = -28А12=(-1)1+2*М12=28 M13 = 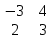 = (-3)·3 - 2·4 = -9 - 8 = -17 = (-3)·3 - 2·4 = -9 - 8 = -17А13=(-1)1+3*М13=-17 M21 = 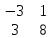 = (-3)·8 - 3·1 = -24 - 3 = -27 = (-3)·8 - 3·1 = -24 - 3 = -27А21=(-1)2+1*М21=-27 M22 = 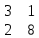 = 3·8 - 2·1 = 24 - 2 = 22 = 3·8 - 2·1 = 24 - 2 = 22А22=22 M23 = 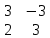 = 3·3 - 2·(-3) = 9 + 6 = 15 = 3·3 - 2·(-3) = 9 + 6 = 15А23=-15 M31 = 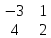 = (-3)·2 - 4·1 = -6 - 4 = -10 = (-3)·2 - 4·1 = -6 - 4 = -10А31=-10 M32 = 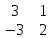 = 3·2 - (-3)·1 = 6 + 3 = 9 = 3·2 - (-3)·1 = 6 + 3 = 9А32=9 M33 = 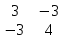 = 3·4 - (-3)·(-3) = 12 - 9 = 3 = 3·4 - (-3)·(-3) = 12 - 9 = 3А33=3 Выпишем матрицу алгебраических дополнений С*= 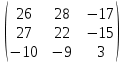 С*Т= 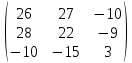 Найдем обратную матрицу А-1=С*Т/det A = 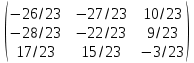 Найти миноры матрицы В В = 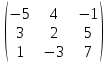 Найдем детерминант матрицы В Det B = 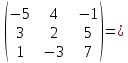 В = В =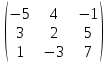 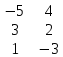 = (-5)*2*7+4*5*1+(- = (-5)*2*7+4*5*1+(-1)*3*(-3)-(-1)*2*1-(-5)*5*(-3)-4*3*7=-198 Определитель матрицы B отличен от нуля, значит обратная матрица B-1 существует. Найдем дополнительные миноры матрицы B. M11= 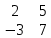 = = 2·7 - (-3)·5 = 14 + 15 = 29 = = 2·7 - (-3)·5 = 14 + 15 = 29M12 = 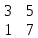 = 3·7 - 1·5 = 21 - 5 = 16 = 3·7 - 1·5 = 21 - 5 = 16M13 = 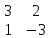 = 3·(-3) - 1·2 = -9 - 2 = -11 = 3·(-3) - 1·2 = -9 - 2 = -11M21 = 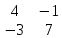 = 4·7 - (-3)·(-1) = 28 - 3 = 25 = 4·7 - (-3)·(-1) = 28 - 3 = 25M22 = 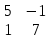 = (-5)·7 - 1·(-1) = -35 + 1 = -34 = (-5)·7 - 1·(-1) = -35 + 1 = -34M23 = 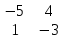 = (-5)·(-3) - 1·4 = 15 - 4 = 11 = (-5)·(-3) - 1·4 = 15 - 4 = 11M31 = 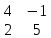 = 4·5 - 2·(-1) = 20 + 2 = 22 = 4·5 - 2·(-1) = 20 + 2 = 22M32 = 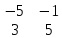 = (-5)·5 - 3·(-1) = -25 + 3 = -22 = (-5)·5 - 3·(-1) = -25 + 3 = -22M33 = 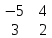 = (-5)·2 - 3·4 = -10 - 12 = -22 = (-5)·2 - 3·4 = -10 - 12 = -22Задание 2 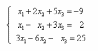 По правилу Крамера Воспользуемся формулой для вычисления определителя матрицы 3×3: ∆ = 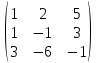 = 1*(-1)*(-1) + 2*3*3 + 5*1*(-6) – 5*(-1)*3 – 1*3*(- = 1*(-1)*(-1) + 2*3*3 + 5*1*(-6) – 5*(-1)*3 – 1*3*(-6) – 2*1*(-1) = 1 + 18 - 30 + 15 + 18 + 2 = 24 ∆1 = 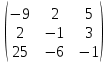 = (-9)·(-1)·(-1) + 2·3·25 + 5·2·(-6) - 5·(-1)·25 - (-9)·3·(- = (-9)·(-1)·(-1) + 2·3·25 + 5·2·(-6) - 5·(-1)·25 - (-9)·3·(-6) - 2·2·(-1) = -9 + 150 - 60 + 125 - 162 + 4 = 48 ∆2 = 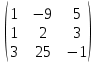 = 1·2·(-1) + (-9)·3·3 + 5·1·25 - 5·2·3 - 1·3·25 - (-9)·1·(- = 1·2·(-1) + (-9)·3·3 + 5·1·25 - 5·2·3 - 1·3·25 - (-9)·1·(-1) = -2 - 81 + 125 - 30 - 75 - 9 = -72 ∆3 = 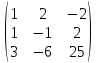 = 1·(-1)·25 + 2·2·3 + (-9)·1·(-6) - (-9)·(-1)·3 - 1·2·(-6) - 2·1·25 = -25 + 12 + 54 - 27 + 12 - 50 = -24 = 1·(-1)·25 + 2·2·3 + (-9)·1·(-6) - (-9)·(-1)·3 - 1·2·(-6) - 2·1·25 = -25 + 12 + 54 - 27 + 12 - 50 = -24X1= ∆1/∆ = 48/24 =2 X2= ∆2/∆ = -72/24=-3 X3= ∆3/∆ = -24/24=-1 Методом Гаусса Перепишем систему в матрицу 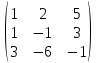 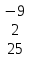 От 2 строки отнимаем 1 строку, умноженную на 1; от 3 строки отнимаем 1 строку, умноженную на 3 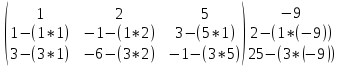 = = 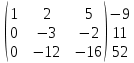 Поделим вторую строку на -3 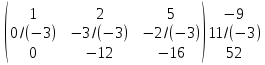 = = 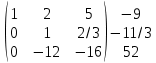 От 1 строки отнимаем 2 строку, умноженную на 2; к 3 строке добавляем 2 строку, умноженную на 12 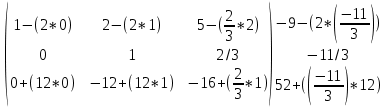 = = 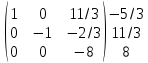 Третью строку делим на -8 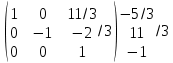 От 1 строки отнимаем третью строку, умноженную на 11/3; от 2 строки отнимаем 3 строку, умноженную на 23 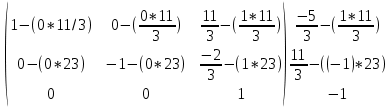 = = 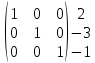 X1= 2 X2= -3 X3= -1 Сделаем проверку 2+2*(-3)+5*(-1)=-9 9=9 2-(-3)+3*(-1)=2 2=2 3*2-6*(-3)-(-1)=25 25=25 Ответ: X1= 2; X2= -3; X3= -1 Задание 3 К 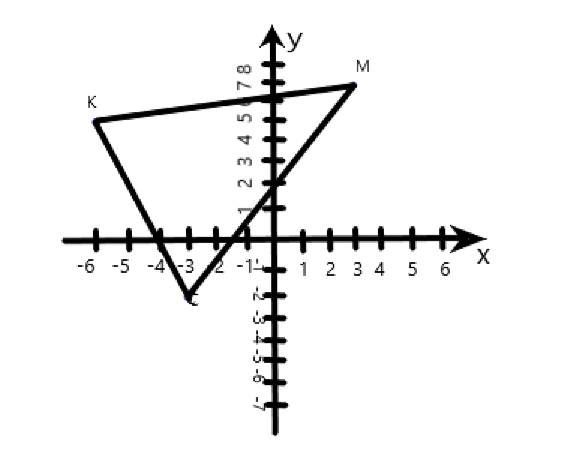 (-6; 5), М(3; 7), С(-3; -2) (-6; 5), М(3; 7), С(-3; -2)Составим уравнение сторон треугольника КМС: КМ: х-хк/хм-хк = у-ук/ум-ук; х-(-6)/3-(-6); х+6/9=у-5/2; 2х-9у+59=0 МС: х-хм/хс-хм = у-ум/ус-ум; х-3/-3-3=у-7/-2-7; х-3/-6=у-7/-9 3х-2у+5=0 КС: х-хк/хс-хк = у-ук/ус-ук; х-(-6)/-3-6=у-5/-2-5; х+6/-9=4-5/7 7х+3у+27=0 Составим систему неравенств т. М в КС: 7*3+3*7+27=21+21+27=69 69>0 т. К в МС: 3*(-6)-2*5+5=-18-10+5=-23 -23<0 т. С в КМ: 2*(-3)-9*(-2)+57=-6+18+57=69 69>0 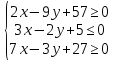 Задание 4 у = х3 + 12х2 + 45х + 50 Найдем область определения функции |
