лабораторная 15. Лабораторная работа 15 (Lr15) магнитные цепи постоянного тока
 Скачать 305.5 Kb.
|
|
Лабораторная работа 15 (Lr15) МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА ЦЕЛЬ РАБОТЫ 1. Ознакомиться с характеристиками ферромагнитных материалов. 2. Провести анализ неразветвлённой магнитной цепи. 3. Приобрести опыт моделирования магнитных цепей постоянного тока в программной среде MS10 и снятия электромагнитных характеристик. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И РАСЧЁТНЫЕ ФОРМУЛЫ 1. НАЗНАЧЕНИЕ И ТИПЫ МАГНИТНЫХ ЦЕПЕЙ Магнитная цепь это совокупность устройств, содержащих ферромагнитные тела, электромагнитные процессы в которых могут быть описаны с помощью понятий магнитодвижущей силы (МДС) F, магнитного потока Ф и разности магнитных потенциалов (магнитного напряжения)Uм. Различают магнитные цепи с постоянными магнитами и магнитные цепи, в которых магнитный поток создаётся постоянным или переменным током, протекающим в одной или нескольких обмотках катушек, размещённых на ферромагнитных сердечниках. Размещение катушек на ферромагнитных сердечниках низкочастотных устройств (f< 1000 Гц) приводит к многократному усилению магнитных потоков и их концентрации в самом ферромагнитном материале, и, как следствие, создаётся нужная конфигурация магнитного поля и магнитной цепи Если вся магнитная цепь выполнена из одного ферромагнитного материала и имеет одинаковое сечение, то она называется однородной Магнитная цепь, содержащая материалы с различными магнитными свойствами или имеющая воздушные зазоры, называется неоднородной. Магнитная цепь, во всех сечениях которой магнитный поток Ф одинаков, называется неразветвлённой В разветвлённой магнитной цепи потоки на различных участках неодинаковы. 2. ПАРАМЕТРЫ СХЕМЫ ЗАМЕЩЕНИЯ МАГНИТНОЙ ЦЕПИ В 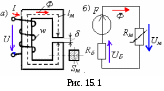 данной лабораторной работе исследуется неразветвлённая неоднородная цепь, имеющая однородный ферромагнитный сердечник и воздушный зазор. Магнитный поток в цепи создаётся магнитодвижущей силой (МДС) F = wI катушки c числом витков w, подключенной к источнику постоянного или линейно изменяющегося напряжения U (рис. 15.1, а). В частности, нужно определить магнитный поток Ф и магнитную индукцию В в воздушном зазоре , если известны: геометрические размеры (длина lм средней магнитной силовой линии (м. с. л.) и площадь поперечного сечения Sм ферромагнитного сердечника, длина воздушного зазора и площадь поперечного сечения S Sм магнитного потока  в зазоре); магнитные свойства магнитопровода (марка стали и её кривая намагничивания B(H)); напряжение U источника питания, число витков w и электрическое сопротивление Rэ катушки. Необходимо также смоделировать в среде MS10 магнитную цепь для снятия характеристики  зависимости магнитной индукции  в зазоре от изменения тока i катушки; оценить долю потерь магнитного напряжения на сердечнике и др.В виду того, что зависимость магнитной индукции В от напряженности магнитного поля H в ферромагнетиках нелинейная, то магнитные цепи, как правило, являются нелинейными, и все расчёты магнитных цепей ведут с определённой степенью точности с использованием графо-аналитических методов. В основе расчёта магнитных цепей лежит закон полного тока, который для магнитной цепи (рис. 15.1, а) записывают в следующем виде:  где Нм и lм напряжённость магнитного поля и длина средней м. с. л. в сердечнике; Ни напряжённость магнитного поля и длина воздушного зазора; F= wI МДС катушки; I ток в катушке. Заменив  и  , получим  где  ( и  ) магнитный поток в сердечнике, Вб;  и  магнитные напряжения на ферромагнитном сердечнике и воздушном зазоре, А;  нелинейное магнитное сопротивление сердечника, 1/Гн;  линейное сопротивление воздушного зазора, 1/Гн;  Гн/м магнитная проницаемость пустоты.Последнему уравнению соответствует схема замещения магнитной цепи (рис. 15.1, б), состоящая из источника МДС F, нелинейного  и линейного  магнитных сопротивлений, на зажимах которых при прохождении потока Ф создаются магнитные напряжения и .3. РАСЧЁТ МАГНИТНОЙ ЦЕПИ ГРАФИЧЕСКИМ МЕТОДОМ В качестве примера определим магнитный поток Ф и магнитную индукцию В в воздушном зазоре; магнитные напряжения  и  на элементах цепи (рис. 15.1, а) для варианта N = 36, соответствующего номеру записи фамилии студента в учебном журнале группы.Определим материал ферромагнетика, заданный числом k, и параметры схемы замещения цепи (рис. 15.1, б), заданные формулами:  (литая сталь 10895, рис. 15.2), где int() – целая часть числа;lм = 0,5 +  м; = 4k10-4, м = 16104 м; = 10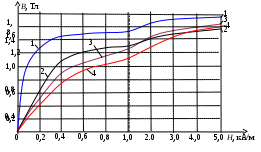k10-4 , м2 = 40104 м2;  , В = 50 + 32 = 82 В (постоянное напряжение на катушке); Ом  Ом (электрическое сопротивление катушки); I=  82/62 1,323 А (ток в катушке); w  = 500 + 50k = 500 + 200 = 700 (число витков обмотки катушки). Н Материал: 1- электротехническая сталь 3411 (листовая холоднокатаная); 2 - электротехническая сталь 1512 (листовая горячекатаная); 3 - электротехническая сталь 1212 (листовая горячекатаная); 4 - литая сталь 10895 Рис. 15,2 аходим МДС обмотки F = wI = 7001,323 = 926 А и магнитное сопротивление зазора  1/Гн.Магнитное напряжение на воздушном зазоре  При  магнитный поток 2,9103 Вб, а при Ф = 0 ( и  )  А.Строим (на одном рисунке 15.3) отражённую характеристику 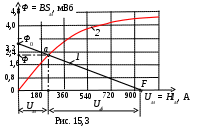 воздушного зазора (прямую линию 1) по двум точкам с координатами [Ф0; 0] и [0; F], и вебер-амперную характеристику  ферромагнитного сердечника 2, заменив магнитные величины В и Н на осях кривой В(Н) соответственно величинами Ф и Uм, умножая значения магнитной индукции В на площадь Sм поперечного сечения сердечника, а значения напряжённости м агнитного поля Н на длину lм средней м. с. л. в сердечнике. Прямая, соединяющая две точки Ф0 и F, пересекает кривую Ф(Uм) в точке а, горизонталь через которую дает на оси ординат искомый магнитный поток Ф 2,2 мВб, а вертикаль позволяет определить на оси абсцисс магнитные напряжения Uм 220 А и U 700 А. Магнитная индукция В в воздушном зазоре  Тл.4. МОДЕЛИРОВАНИЕ И РАСЧЁТ ПАРАМЕТРОВ ЭЛЕМЕНТОВ МАГНИТНОЙ ЦЕПИ ПО ПРОГРАММЕ MS10 С 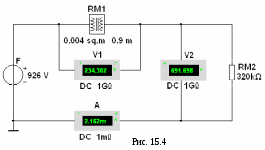 оберём схему магнитной цепи (см. рис. 15.1, б) на рабочем поле среды MS10, состоящей из источника постоянного напряжения F, имитирующего источник МДС F; нелинейного элемента RM1, моделирующего ферромагнитный сердечник, и резистора RM2, сопротивление которого равно магнитному сопротивлению Rвоздушного зазора (рис. 15.4). Для измерения магнитного потока Ф используется амперметр А (режим DC, внутреннее сопротивление RА = 1 мОм), а для измерения магнитных напряжений на ферромагнитном сердечнике и воздушном зазоре – вольтметры V1 и V2 (режим DC, внутренние сопротивления RV = 1 ГОм). В качестве элемента RM1 использован имеющийся в библиотеке Basic среды MS10 магнитный элемент (Мagnetic Core), в диалоговом окне которого необходимо ввести геометрические размеры сердечника и 8…12 координатных точек (см. табл. 15.1) кривой намагничивания В(Н) материала сердечника (в рассматриваемом примере для литой стали 10895 число k = 4): площадь поперечного сечения сердечника (Cross-sectional area) Sм = 0,004 м2; длина средней м. с. л. в сердечнике (Core length) lм = 0,9 м; число координатных точек таблицы кривой намагничивания В(Н) (Numder of co-ordinаte) 10: напряжённость магнитного поля в первой точке (Magnetic field co- ordinate1) Н1 = 0; магнитная индукция в первой точке (Flux density co-ordinate 1) В1 = 0; напряжённость магнитного поля во второй точке (Magnetic field co ordinate 2) Н2 = 100 А; магнитная индукция во второй точке (Flux density co-ordinate 2) В2 = 0,25 Вб/м2; …………………………………………………………………………… напряжённость магнитного поля в десятой точке (Magnetic field co- ordinate 10) Н10 = 5000 А; магнитная индукция в десятой точке (Flux density co-ordinate 10) В10 = 1,6 Вб/м2. Т а б л и ц а 15.1
Результаты моделирования и расчёта магнитной цепи по программе MS10 (см. рис. 15.4) соответствуют магнитным величинам, рассчитанным графическим методом в п. 3 раздела "Теоретические сведения …". УЧЕБНЫЕ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИХ ВЫПОЛНЕНИЮ Задание 1. Рассчитать графическим методом магнитную цепь (см. рис. 15.1, а), определив магнитный поток Ф и магнитную индукцию В в воздушном зазоре; магнитные напряжения  и  на элементах цепи (см. рис. 15.1, б) для варианта N, соответствующего номеру записи фамилии студента в учебном журнале группы. Параметры элементов схемы определить по формулам, приведенным в п. 3 раздела "Теоретические сведения …".Задание 2. Запустить лабораторный комплекс Labworks и программную среду МS10 (щёлкнув мышью на команде Эксперимент меню комплекса Labworks). Открыть файл 15.4.ms10, размещённый в папке Circuit Design Suite 10.0, с моделью магнитной цепи постоянного тока и установить рассчитанные в Задании 1 параметры элементов схемы и данные табл. 15.1. Результаты расчёта и моделирования (показания приборов) занести в самостоятельно составленную таблицу. Сравнить полученные результаты моделирования с расчётными значениями электрических и магнитных величин. Оценить долю потерь магнитного напряжения на сердечнике от МДС F источника. Снять характеристики  и  зависимости магнитного потока и магнитного напряжения на воздушном зазоре цепи от длины зазора (получить не менее четырех координатных точек, в т. ч. при 0,5; 1; 1,5 и 2 соответственно при RM2 = 160; 320; 480 и 640 кОм для варианта 36). Результаты моделирования занести в самостоятельно составленную в отчёте таблицу. Построить графики и и определить, во сколько раз снижается магнитный поток в зазоре при увеличении его длины в два раза (от = 1,6 мм до = 3,2 мм для варианта 36)?Задание 3. Открыть файл 15.5.ms10, размещённый в папке Circuit Design Suite 10.0, или собрать схему магнитной цепи (рис. 15.5, а) на рабочем поле программной среды MS10 для снятия вебер-амперной характеристики Ф(i) или характеристики  зависимости магнитной индукции B = Ф/S в зазоре от тока iкатушки. Для этого: заменить источник постоянного напряжения F (см. рис. 15.4) генератором линейно изменяющегося напряжения XFG1 и включить его в схему замещения катушки (левый контур, рис. 15.5, а), содержащей резистор Re с электрическим сопротивлением обмотки Re = Rэ, зависимый источник напряжения INUT1, управляемый током i= Uэ/Rэ катушки, с коэффициентом передачи, равным 1, и зависимый источник напряжения INUT2, управляемый током i= Uэ/Rэ катушки, с коэффициентом передачи, равным числу витков w катушки. При этом в схеме замещения магнитной цепи в правом контуре рис. 15.5, а действует МДС F = wi; для наблюдения графика зависимости  на экране осциллографа на вход его канала А подать напряжение, численно равное току i катушки от источника INUT1, а на вход канала В напряжение, пропорциональное магнитной индукции В, снимаемое с выходных зажимов зависимого источника напряжения INUT3, управляемого током магнитным потоком Ф = F/(R + Rм) = wI/(R+ Rм) с 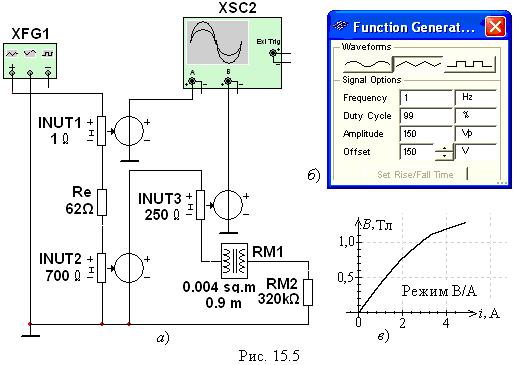 коэффициентом передачи, равным 1/Sм; установить параметры элементов схемы, рассчитанные или полученные при выполнении предыдущих заданий, и режимы функционирования источников питания и осциллографа (см. рис. 15.5, а и б для примера, рассмотренного в п. 3 раздела "Теоретические сведения …"); запустить программу MS10. Установить режим В/А работы осциллографа, см. рис. 15.5, в). Скопировать график функции В(i) на страницу отчёта и определить ток в катушке, при котором магнитная индукция в зазоре в 1,5 раза больше значения индукции Вδр, рассчитанного в п. 3 раздела "Теоретические сведения …"; определить диапазон допустимых значений тока, в пределах которого зависимость В(i) катушки с ферромагнитным сердечником можно считать линейной; задать режим Y/T работы осциллографа и установить его визирную линию 1 на значении тока катушки, рассчитанного в п. 3 раздела "Теоретические сведения …". Проверить, равно ли значение магнитной индукции значению Вδр? Вторую визирную линию осциллографа установитьна значении магнитной индукция в зазоре Вδ = 1,5Вδр. Проверить, равно ли необходимое для этого режима работы цепи значение тока катушки найденному значению при функционировании осциллографа в режиме B/A? С 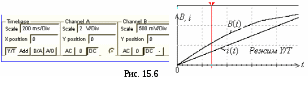 копировать графики функций B(t) и i(t) (см. рис. 15.6) на страницу отчёта. СОДЕРЖАНИЕ ОТЧЁТА1. Наименование и цель работы. 2. Расчётные и экспериментальные схемы магнитных цепей с исходными значениями параметров. 3. Расчётные формулы и вычисления. Таблицы с занесенными предварительно вычисленными и измеренными физическими величинами. 4. Графики характеристик B(t) и и зависимости В(i) с оцифровкой шкал осей и характерных точек; копии осциллограмм В(t) и  .5. Выводы по работе. ТЕСТОВЫЕ ЗАДАНИЯ К РАБОТЕ 151. Укажите, как и во сколько раз изменится магнитное сопротивление ферромагнитного сердечника при уменьшении его поперечного сечения в 2 раза? Увеличится Уменьшится Не Увеличится Увеличится в 4 раза в 2 раза изменится в 2 раза в 8 раз  2. Укажите единицы магнитного сопротивления, магнитного напряжения и МДС: Ом; В; А 1/Гн; А; А 1/Гн; В; Вб Ом; А; А 1/Гн; В; Тл 3. Укажите, какое влияние на изменение тока в катушке оказывает нелинейность магнитной характристики замкнутого ферромагнитного сердечника при её подключении к источнику постоянного напряжения? Замедляет процесс нарастания тока в начале и ускоряет его в конце переходного процесса. Обеспечивает равномерность нарастания тока. Ускоряет процесс нарастания тока в начале и замедляет его в конце переходного процесса.4. Укажите, во сколько раз различаются магнитные сопротивления равномерно намагниченного сердечника (с = 1000) и воздушного зазора, если длина средней магнитной силовой линии lм = 20 см, длина воздушного зазора = 0,1 см, и что в силу малости воздушного зазора магнитный поток в нём проходит сквозь сечение, равное сечению сердечника? в 2 раза в 20 раз в 100 раз в 200 раз 5. Укажите, как изменится магнитное напряжение на ферромагнитной части магнитопровода катушки, если увеличить в нём воздушный промежуток (зазор)? Уменьшится Не изменится Увеличится 6. Укажите, во сколько раз уменьшится магнитный поток в цепи с ферромагнитным сердечником, если воздушный зазор увеличить в два раза (с = 1000 = const, длина средней м. с. л. lм = 20 см в сердечнике, длина воздушного зазора = 0,1 см, и что в силу малости воздушного зазора магнитный поток в нём проходит сквозь сечение, равное сечению сердечника)? в 4,15 раз в 3,33 раз в 1,33 раз в 1,15 раз 7. На кольцевой замкнутый сердечник из дерева равномерно намотана обмотка с числом витков w = 2000. Поперечное сечение сердечника Sм= 410-4 м2, длина средней м. с. л. в сердечникеlм = 0,2 м. Укажите значение тока в обмотке катушки, при котором магнитный поток в сердечнике Ф = 110-5 Вб. 1 А 2 А 3 А 4 А 5 А | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||