Лабораторная работа р 16. Лаб.16-3. 15..DOC. Лабораторная работа 16 б207
 Скачать 141 Kb. Скачать 141 Kb.
|
|
Лабораторная работа 16-3. Б-207. Определение ЭДС гальванического элемента. Цель работы: Методом компенсации измерить ЭДС гальванического элемента. Приборы и принадлежности: Эталонный элемент Вестона, гальванический элемент, реостат, нуль-гальванометр, ключи. А. Основные понятия. 1. ЭЛЕКТРИЧЕСКИЙ ТОК. Если изолированный проводник поместить в электрическое поле Е, то на свободные заряды q в проводнике будет действовать сила F = q E. В проводнике может при определенных условиях возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда.
Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле. Чтобы электрический ток в проводнике существовал длительное время, необходимо все это время поддерживать в нем электрическое поле. Электрическое поле в проводниках создается и может длительное время поддерживаться источниками электрического тока. В настоящее время человечество использует четыре основные источника тока: статический, химический, механический и полупроводниковый (солнечные батареи), но во всяком из них совершается работа по разделению положительно и отрицательно заряженных частиц. Раздельные частицы накапливаются на полюсах источника тока, так называют места, к которым с помощью клемм или зажимов подсоединяют проводники. Один полюс источника тока заряжается положительно, другой - отрицательно. Если полюсы соединить проводником, то под действием поля свободные заряженные частицы в проводнике будут двигаться, возникнет электрический ток. 2. СИЛА И ПЛОТНОСТЬ ТОКА. Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника за интервал времени Δt, к этому интервалу времени: I = ∆q/∆t. Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока I = Q/t, где Q - электрический заряд, проходящий за время t через поперечное сечение проводника. В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током. Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Величина, определяемая силой тока, проходящей через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока: j = dI/dS. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е, то за время t через поперечное сечение S проводника переносится заряд dQ = ne а плотность тока j = ne 3. СТОРОННИЕ СИЛЫ. Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачки жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток. При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
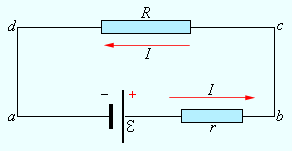
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника ЭДС. E = A/Q. Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину Е можно также называть электродвижущей силой источника тока, включенного в цепь. Сторонняя сила Fст, действующая на заряд Q, может быть выражена как: Fст = Ест Q0, где Ест — напряженность поля сторонних сил. Работа же сторонних сил по перемещению заряда Q0 на замкнутом участке цепи равна A = ò Fстdl = Q0ò Eст dl. Разделив это выражение на Q0, получим выражение для Э.Д.С., действующей в цепи:Е = ò Eст dl, т.е. Э.Д.С., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Э.Д.С., действующая на участке 1 — 2 равна Е1-2 = 1ò 2Ест dl. На заряд Q0 помимо сторонних сил действуют также силы электростатического поля Fe = Q0E. Таким образом, результирующая сила, действующая в цепи на заряд Q0 равна F = Fст + Fe = Q0(Eст + E). Работа, совершаемая результирующей силой над зарядом Q0 на участке 1 — 2 равна А1-2 = Q0 1ò 2Ecт dl + Q0 1ò 2E dl. Можно также записать А1-2 = Q0E12 + Q0(j1 - j2). Для замкнутой цепи работа электростатических сил равна нулю, следовательно: А1-2 = Q0E 12. Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических и сторонних сил при перемещении единичного заряда на данном участке цепи. U12 = j1 - j2 + E. Понятие напряженности является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов, если на этом участке не действует Э.Д.С. Участок цепи, на котором действуют сторонние силы, называют неоднородным. Участок цепи, на котором отсутствуют сторонние силы, называют однородным. 4. ЗАКОН ОМА. Сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника: I = U/R, где R - электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи (не содержащей Э.Д.С.). Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. В СИ единицей электрического сопротивления проводников служит Ом. Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками) изображается прямой линией, проходящей через начало координат. Для участка цепи, содержащего ЭДС, закон Ома записывается в форме: IR = U12 = φ1- φ2 + ε = ∆φ12 + ε. Это соотношение принято называть обобщенным законом Ома. Для замкнутой цепи постоянного тока, один цепи (cd) является однородным, а другой (ab), содержит источник тока с ЭДС, равной ε. Сложив равенства, получим: I(R + r) = ∆φcd + ∆φab + ε. Но ∆φcd = ∆φab = - ∆φab . Поэтому I = ε/(R + r). Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного учасков цепи.
Рис. 3. Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 - режим короткого замыкания. Сопротивление r неоднородного участка можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R << r), тогда в цепи потечет ток короткого замыкания: Ikz = ε/r. Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику подсоединяется некоторое внешнее балластное сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего балластного сопротивления. Если внешняя цепь разомкнута, то Δφba – Δφab = ε, т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС. Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной .∆φba = ε – Ir. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
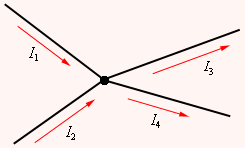
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры. Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение. Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. 5. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого сделан проводник. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S: R = .l/S, где - коэффициент пропорциональности, характеризующий материал проводника. Он называется удельным электрическим сопротивлением. Наименьшим удельным сопротивлением обладают медь и серебро. 6. ПРАВИЛА КИРХГОФА ДЛЯ РАЗВЕТВЛЕННЫХ ЦЕПЕЙ. Любая точка разветвления цепи, в которой сходится не менее трех проводников, называется узлом. Ток, входящий в узел — положительный, а ток, выходящий — отрицательный. Первое правило Кирхгофа: Алгебраическая сумма токов, сходящихся в узле, равна нулю: Ii = o.
Второе правило Кирхгофа получается из обобществленного закона Ома для разветвленных цепей. I1R1 - I2R2 + I3R3 = E1 + E2 + E3
В любом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил тока Ii на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме Э.Д.С. встречающихся в этом контуре: IiRi = Ei. При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1. Выбрать одно направление токов на всех участках цепи. 2. Выбрать одно направление обхода контура и строго его придерживаться. 3. Составить столько уравнений, чтобы их число было равно числу искомых величин: каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах. Контрольные вопросы. .Что такое электрический ток? Что такое сторонние силы? Сформулируйте закон Ома для однородного участка цепи, для неоднородного участка цепи, для полной цепи. Дайте определение разности потенциалов, напряжения и ЭДС источника тока и каким образом они связаны между собой? Запишите правила Кирхгоффа и условия их применения? Сформулировать правило знаков для первого и второго правил Кирхгофа. Методика и техника эксперимента.В работе проводится измерение ЭДС гальванического элемента путем сравнения с эталонного элемента. Метод измерения называется методом компенсации. Схема метода компенсации показана на рисунке. В нее входят три гальванических элемента с электродвижущими силами εх и εэт, внутренними сопротивлениями r1 и r2, гальванометр и переменный резистор, включенный в участок цепи АВС. Два плеча переменного резистора АВ и ВС имеют сопротивления R1 и R2 соответственно и их величины могут изменяться. При изменении сопротивлений R1 и R2 их сумма R1 + R2 остается постоянной. Поставим тумблер К1 в положение εэт и замкнем кнопку К2. Рассмотрим образовавшуюся электрическую цепь. Обозначим величины токов, текущих по участкам цепи, I, I1 и I2. Запишем первое правило Кирхгофа для узла В (- I – I1 + I2) = 0, а также второе правило Кирхгофа для контура ВεэтDC (I1r2 + I2R1) = εэт и для контура АεDCВ (Ir + IR2 + I2R1) = εэт.Изменяя сопротивления R1 и R2 плеч переменного резистора, можно добиться того, что ток через гальванометр перестанет течь, то есть I1 =0. Тогда I = I2 и из уравнения следует, что IR1 = εэт.. Это означает, что если сила тока, проходящего через источник εэт, равна нулю, то падение напряжения на участке цепи ВCD, параллельно которому присоединен этот источник, равно электродвижущей силе εэт. Подставив в уравнение (3) значение тока I2 = I = εэт /R1, получим εэт.=(εR1)/(r + R2 + R1). Теперь включим вместо эталонного источника εэт гальванический элемент с неизвестной ЭДС εх. Изменяя сопротивления плеч переменного резистора, добьемся вновь отсутствия тока через гальванометр. Теперь сопротивления участков цепи АВ и ВС будут равны соответственно R11 и R11, причем ( R21 + R11).= (R2 + R1). 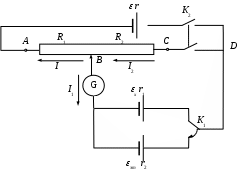 Рис. 7. Для новой цепи будет справедливо равенство εx.= (εR1)/(r + R2 + R1). Из соотношений (4) и (5) получим εx./εэт.= (Rx/Rэт.). Отсюда можно определить неизвестную ЭДС εх, измеряя сопротивления R1 и R1. Отметим, что величина ЭДС, вспомогательного источника ε не входит в окончательный результат. Необходимо лишь, чтобы значение ε во время измерений было постоянным и превышало ЭДС сравниваемых элементов. В данной работе в качестве переменного резистора (участок цепи АВС) используется реостат. В точке В схемы находится подвижный контакт, позволяющий изменять сопротивления плеч АВ и ВС. В такой схеме сопротивление участка ВС (R1) пропорционально длине этого участка, поэтому выражение (6) можно привести к виду. Ex =Eэт. (l1/l2). Порядок выполнения работыУстановить тумблер К1 на измерительном стенде в положении εэт Нажав на кнопку К2 , перемещать подвижный контакт В реостата до тех пор, пока гальванометр не покажет отсутствия тока. Измерить длину l участка реостата ВС. Переключить тумблер К1 в положение εх . Выполнить пункт 2. Измерить длину l участка реостата ВС. Результаты измерений записать в таблицу. Вычислить ЭДС исследуемого элемента по формуле (7). Рассчитайте погрешность измерений ΔЕх, используя выражение: ∆Ex = (Eэт./lср.)∆l.√(1 + (l1/l2). ∆l1 = ∆l2 = (lk/2), где lk- ширина контакта. Запишите окончательный результат в виде: Еx = (Еср. ± ΔЕх) В  ОТЧЕТ. Лабораторная работа №. 16-3. Б-207. Определение ЭДС гальванического элемента. Цель работы: познакомиться с одним из методов измерений электродвижущей силы, измерить ЭДС гальванического элемента. Основные расчетные формулы. Ex =Eэт. (l1/l2). ∆Ex = (Eэт./lср.)∆l.√(1 + (l1/l2). ∆l1 = ∆l2 = (lk/2), где lk- ширина контакта. Запишите окончательный результат в виде: Еx = (Еср. ± ΔЕх) В Таблица 1.
Дата. Подпись. |