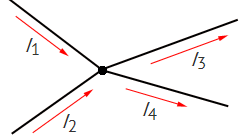
1. Условия возникновения тока. Эдс источника тока. Напряжение. Условия
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
Т.2) Полученные опытным путем значения электропроводности g дают для средней длины свободного пробега электронов в металлах величину порядка сотен междоузельных расстояний. Это гораздо больше, чем по классической теории. 6. Энергетические зоны в кристаллах. Собственная и примесная проводимости полупроводников. Квазичастицы – электроны проводимости и дырки. Энергозоны Согласно квантовой теории энергия электронов в атомах или молекулах квантуется, т. е. может принимать только некоторые дискретные значения, разделенные конечными промежутками. Эти значения называются уровнями энергии. Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах. По мере сближения атомов между ними возникает все усиливающееся взаимодействие, которое приводит к изменению положения уровней. В результате вместо одного одинакового для всех N атомов уровня возникают N очень близких, но не совпадающих уровней. Таким образом, каждый уровень изолированного атома расщепляется в кристалле на N густо расположенных уровней, образующих энергетическую полосу или зону. Проводимости Различают собственные и примесные полупроводники. К числу собственных относятся чистые полупроводники (без примесей или с очень малой концентрацией примеси, что не оказывает существенного влияния). Проводимость таких чистых полупроводников называется собственной. В примесных полупроводниках электрические свойства определяются примесями, вводимыми искусственно в очень малых количествах. Например, введение в кремний всего лишь 0,001% бора увеличивает его проводимость при комнатной температуре примерно в 1000 раз. Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью. Примесная проводимость возникает, если некоторые атомы в узлах решётки полупроводников замещены атомами, валентность которых отличается на единицу от валентности основных атомов. Для установления связи с четырьмя ближайшими соседями атом мышьяка использует 4 валентных электрона (рис.7а). Пятый электрон в образовании связей не участвует. Он связан со своим атомом слабее. Энергия связи его составляет Дырки В валентной зоне освобождаются квантовые состояния, не занятые электронами. Такие квантовые состояния получили весьма неудачное название дырок. Квазичастицы (как бы существующие) дырки также являются носителями электрического тока. Действительно, при наличии дырок электроны могут рекомбинировать с ними, т. е. совершать квантовые переходы из каких-то квантовых состояний в незаполненные состояния, т. е. дырки. Прежние заполненные состояния при этом освобождаются, т. е. превращаются в дырки. Последние в свою очередь могут рекомбинировать с другими электронами с образованием новых дырок и т. д. 7. (p-n) – переход. ВАХ (p-n) перехода. Электронно дырочный переход(p-n переход) - область соприкосновения двух полупроводников с разными типами проводимости — дырочной.Поскольку в р-области концентрация дырок гораздо выше, чем в n-области, дырки из n -области стремятся проникать в электронную область. Электроны проникать в р-область. Прямое смещение - Происходит когда внешнее напряжение противонаправлено существующему в переходе полю -> динамическое равновесие нарушается, и диффузионный ток преобладает над дрейфовым током, быстро нарастая с повышением напряжения. (Возвращается к начальном состоянию) Обратным смещением - Происходит когда внешнее напряжение сонаправлено с полем в переходе -> это приведёт лишь к увеличению толщины слоёв пространственного заряда. Диффузионный ток уменьшится настолько, что преобладающим станет малый дрейфовый ток. (усиливает переходы) Вольт-амперная характеристика p-n перехода. Вольт-амперная характеристика (ВАХ) p-n-перехода представляет собой зависимость тока от величины и полярности приложенного напряжения и описывается выражением: 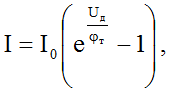 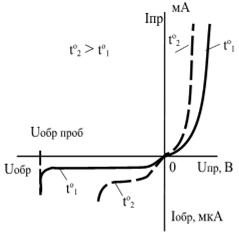 где I0 – тепловой обратный ток p-n-перехода; Uд – напряжение на p-n-переходе; jт = k T/ q – тепловой потенциал, равный контактной разности потенциалов (jк) на границе p-n-перехода при отсутствии внешнего напряжения (при T = 300 К, jт = 0,025 В); k – постоянная Больцмана; T – абсолютная температура; q –заряд электрона. 8. Контактные явления. Эффект Зеебека. Эффект Пельтье. Эффект Томсона. Как показывает опыт, на контакте двух различных металлов образуется двойной электрический слой и соответствующая разность потенциалов (рис. 6.8). 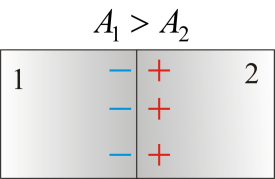 Появление двойного электрического слоя обусловлено различием работ выхода электронов из металлов. Чем она больше, тем меньше вероятность перехода электронами границы раздела. Поэтому со стороны металла с большей работой выхода накапливается отрицательный заряд, а с противоположной – положительный. Законы Вольта. 1. На контакте двух разных металлов возникает разность потенциалов, которая зависит от химической природы и от температуры спаев. 2. Разность потенциалов на концах последовательно соединенных проводников не зависит от промежуточных проводников и равна разности потенциалов, возникающей при соединении крайних проводников при той же температуре. Эффект Зеебека — явление возникновения ЭДС в замкнутой электрической цепи, состоящей из последовательно соединённых разнородных проводников, контакты между которыми находятся при различных температурах. В замкнутой цепи, состоящей из разнородных проводников, возникает термо-ЭДС, если места контактов поддерживаются при разных температурах. Цепь, которая состоит только из двух различных проводников, называется термоэлементом илитермопарой.  где где  — термоэлектрическая способность пары — термоэлектрическая способность пары Эффект Пельтье́ —термоэлектрическое явление переноса энергии при прохожденииэлектрического тока в местеконтакта (спая) двух разнородныхпроводников, от одного проводника к другому. Величина перемещённой энергии и направление её переноса зависят от вида контактирующих веществ и от направления исилы протекающего электрического тока[1]:  , ,где: Q — количество выделенного или поглощённого тепла; I — сила тока; t — время протекания тока; Π — коэффициент Пельтье, который связан с коэффициентомтермо-ЭДС α вторым соотношениемТомсона [2] Π = αT , где T — абсолютная температура вK. Причина возникновения явления Пельтье заключается в следующем. На контакте двух веществ имеется контактная разность потенциалов, которая создаёт внутреннее контактное поле. Если через контакт протекает электрический ток, то это поле будет либо способствовать прохождению тока, либо препятствовать. Если ток идёт против контактного поля, то внешний источник должен затратить дополнительную энергию, которая выделяется в контакте, что приведёт к его нагреву. Если же ток идёт по направлению контактного поля, то он может поддерживаться этим полем, которое и совершает работу по перемещению зарядов. Необходимая для этого энергия отбирается у вещества, что приводит к охлаждению его в месте контакта. Эффект Томсона — одно из термоэлектрических явлений, заключающееся в том, что в однородном неравномерно нагретом проводнике с постоянным током, дополнительно к теплоте, выделяемой в соответствии с законом Джоуля — Ленца, в объёме проводника будет выделяться или поглощаться дополнительная теплота Томсона в зависимости от направления тока. Количество теплоты Томсона пропорционально силе тока, времени и перепаду температур, зависит от направления тока. 9. Релятивистская природа магнитного поля. Магнитная индукция. Магнитное поле тока. Закон Био-Савара-Лапласа для расчета магнитных полей линейного и кругового токов. В ряде современных учебных курсов по физике, изданных в течение последнего десятилетия появилось и стремительно распространяется воззрение на магнитное поле как на релятивистский эффект. Магнитное поле трактуется не как самостоятельная физическая материальная сущность и даже не как одна из форм проявления электромагнитного поля, а лишь как процесс, релятивистский эффект, возникающий в пространстве, окружающем точечные заряды, вследствие конечной скорости передачи изменений величины электрического поля через пространство Магнитное поле тока - магнитное поле создаваемое вокруг проводника с током Свойства ( стационарного) магнитного поля 1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами. 2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током. 3. Магнитное поле вихревое, т.е. не имеет источника. Магнитная индукция- это силовая характеристика магнитного поля. Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле Правило буравчика - Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока. Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде 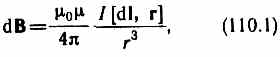 Магнитное поле прямого тока —тока, текущего по тонкому прямому проводу бесконечной длины магнитная индукция поля прямого тока Магнитное поле в центре кругового проводника с током. все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка магнитная индукция поля в центре кругового проводника с током 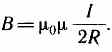 10. Виток с током в однородном и неоднородном магнитных полях. Магнитный момент витка с током. Магнитный момент – векторная величина, направленная по нормали к контуру n. К контуру можно построить нормали в двух направлениях. За положительное направление нормали принято считать направление, связанное с током правилом правого винта Виток с током I характеризуется магнитным моментом: pm = IS, (4) (ISn - если векторно, т.к. n нормаль) где S – площадь витка. Момент сил, вращающий рамку в магнитном поле с индукцией В, рассчитывается по формуле: M=pmB·sin α Если виток с током поместить в неоднородное магнитное поле, то в различных его местах магнитная индукция будет иметь различные значения и направления. Силы, действующие на разные стороны повернувшегося витка, теперь не будут полностью компенсировать друг друга. Они направлены перпендикулярно силовым линиям. Силовые линии не параллельны, поэтому силы не будут находиться в одной плоскости с витком. Появится равнодействующая сил, направленная в сторону возрастания магнитной индукции. Виток начнет втягиваться в область более сильного поля или наоборот начнет выталкиваться и перемещаться в область более слабого поля в зависимости от направления тока. Если магнитный момент витка направлен вдоль силовой линии, то силу, действующую на виток в неоднородном поле, можно рассчитать по формуле: pm – магнитный момент рамки, 11. Действие магнитного поля на токи и свободные заряды. Взаимодействие параллельных токов. Закон Ампера. Зако́н Ампе́ра — закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы dF , с которой магнитное поле действует на элемент объёма dV проводника с током плотности j , находящегося в магнитном поле с индукцией B , в СИ имеет вид: 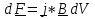 12. Магнитное поле движущегося заряда. Сила Лоренца. Силу, с которой магнитное поле действует на движущуюся заряженную частицу, называют силой Лоренца Сила F, действующая на частицу с электрическим зарядом q , движущуюся со скоростью v , во внешнем электрическом E и магнитном B полях, такова: F = q(E+v*B) 13. Движение заряженных частиц в магнитном поле. Эффект Холла. Применения эффекта Холла. Пусть по проводнику прямоугольного поперечного сечения (b – ширина, а – толщина образца) течет постоянный электрический ток, I – сила тока. Если образец поместить в однородное магнитное поле, перпендикулярное двум его граням, то между двумя другими гранями возникает разность потенциалов. Это явление было обнаружено Холлом и называется эффектом Холла. Разность потенциалов между гранями называется эдс Холла В случае металлической пластинки носителями тока являются электроны . При включении магнитного поля на каждый носитель тока действует сила Лоренца В результате действия этой силы носители тока смещаются в поперечном направлении. На одной грани пластинки образуется избыток отрицательных зарядов, а на другой соответственно избыток положительных. Таким образом, появляется дополнительное поперечное электрическое поле, напряженность Эффект Холла нашел множество областей применения. Эффект Холла позволяет определить концентрацию и подвижность носителей заряда.На основе эффекта Холла работают датчики Холла — приборы, измеряющие напряжённость магнитного поля.Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей и МГД генераторы 14. Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля. Магнитный поток Фт сквозь произвольную поверхность S находится суммированием или интегрированием всех элементарных потоков: Фт =∫BdS cos В,n) = ∫ Вп dS = \B dS Теорема Остроградского—Гаусса применительно к магнитному полю утверждает: магнитный поток сквозь произвольную замкнутую поверхность равен нулю: ∫Вп dS = 0 15. Работа по перемещению проводника и контура с током в магнитном поле. Циркуляция . МП совершает работу по перемещению проводника с током dA = FAdx= IBAdx= IBdS= IdФ Работа по перемещению замкнутого контура с током в МП равна произведению силы тока в контуре на приращение магнитного потока, сцепленного с контуром. Циркуляцией вектора B индукции магнитного поля вдоль замкнутого контура L называется интеграл вида
где L — контур произвольной формы, dl — элемент длины контура в направлении его обхода. Интегрирование распространено на всю длину замкнутого контура. 16. Закон полного тока для магнитного поля в вакууме и его применение к расчету магнитного поля тороида и соленоида. Магнитные цепи. Закон полного токамагнитного поля в вакууме: циркуляция вектора индукциимагнитного поля постоянного электрического тока вдоль замкнутого контура пропорциональна алгебраической сумме токов, охватываемых этим контуром: ∫В dl = ∫Вl dl = μ0∑Ik где n - число всех проводников с токами, охватываемых контуром L произвольной формы. Токи считаются положительными, если из конца вектора плотности тока, направленного по оси проводника в сторону тока, обход контура L кажется происходящим против часовой стрелки. В противном случае токи считаются отрицательными. Токи, которые не охватываются контуром L, не влияют на циркуляцию B. Магнитную индукцию поля, созданного постоянным током I, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси можно определить, применяя теорему о циркуляции вектора индукции. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно теореме равна ∫ Вl dl=μ0NI. Отсюда приходим к выражению для магнитной индукции поля внутри соленоида в вакууме: B = μ0Nl/l магнитная индукция внутри тороида (в вакууме) равна B = μ0Nl/(2πr) Магнитной цепью называется совокупность устройств, содержащих ферромагнитные тела, служащих для сосредоточения магнитного потока в определённой части пространства. В силу непостоянства магнитной проницаемости µ магнитные цепи нелинейны. Если магнитная цепь выполнена из одного ферромагнитного материала, то её называют однородной, если из различных материалов – неоднородной. Магнитная цепь, во всех сечениях которой магнитный поток одинаков, называется неразветвлённой магнитной цепью. 17. Явление электромагнитной индукции. Опыты Фарадея. Закон Ленца. Явление электромагнитной индукции. Оно говорит о том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного. Приведем классические опыты Фарадея, с помощью которых было открыто явление электромагнитной индукции. Опыт I (рис. 1а). Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид. Опыт II. Концы одной из катушек, которая вставлена одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. В моменты включения или выключения тока наблюдается отклонение стрелки гальванометра, а также в моменты его уменьшения или увеличения, а также при перемещении катушек друг относительно друга (рис. 1б). Направления отклонений стрелки гальванометра также имею противоположные направления при включении или выключении тока, его увеличении или уменьшении, приближении или удалении катушек. 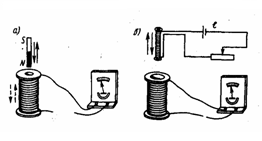 Правило Ленца определяет направление индукционного тока и гласит: Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток. Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца. 18. Закон электромагнитной индукции и его вывод из закона сохранения энергии, также на основе электронной теории. Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции: Знак минусопределяется правилом Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток. Закон Фарадея может быть непосредственно получен из закона сохранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоскости контура, и может свободно перемещаться. Под действием силы Ампера F, направление которой показано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампера производит работу dA=IdФ, где dФ — пересеченный проводником магнитный поток. Согласно закону сохранения энергии, работа источника тока за время dt ( где R — полное сопротивление контура. Тогда где -dФ/dt=ξi есть не что иное, как закон Фарадея 19. Само- и взаимоиндукция. Индуктивность. Токи при замыкании и размыкании цепи. Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца(закону) препятствует изменению тока в контуре. Магнитный поток пронизывающий катушку (Φ = LI) Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна Еще про самоиндукцию. Изменяющийся по величине ток всегда создает изменяющееся магнитное поле, которое, в свою очередь, всегда индуктирует ЭДС. При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется ЭДС самоиндукции. Когда ЭДС в катушке индуктируется за счет изменения собственного магнитного потока, величина этой ЭДС зависит от скорости изменения тока. Чем больше скорость изменения тока, тем больше ЭДС самоиндукции. Величина ЭДС самоиндукции зависит также от числа витков катушки, густоты их намотки и размеров катушки. Чем больше диаметр катушки, число ее витков и густота намотки, тем больше ЭДС самоиндукции. Эта зависимость ЭДС самоиндукции от скорости изменения тока в катушке, числа ее витков и размеров имеет большое значение в электротехнике. Направление ЭДС самоиндукции определяется по закону Ленца. ЭДС самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока. Иначе говоря, убывание тока в катушке влечет за собой появление ЭДС самоиндукции, направленной по направлению тока, т. е. препятствующей его убыванию. И, наоборот, при возрастании тока в катушке возникает ЭДС самоиндукции, направленная против тока, т. е. препятствующая его возрастанию. Не следует забывать, что если ток в катушке не изменяется, то никакой ЭДС самоиндукции не возникает. Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку с железным сердечником, так как железо значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции при его изменении. Индуктивность (L) Итак, нам известно, что величина ЭДС самоиндукции в катушке, кроме скорости изменения тока в ней, зависит также от размеров катушки и числа ее витков. Следовательно, различные по своей конструкции катушки при одной и той же скорости изменения тока способны индуктировать в себе различные по величине ЭДС самоиндукции. Чтобы различать катушки между собой по их способности индуктировать в себе ЭДС самоиндукции, введено понятие индуктивности катушек, или коэфициента самоиндукции. ЭДС взаимоиндукции Итак, мы знаем, что ЭДС индукции в катушке можно вызвать и не перемещая в ней электромагнит, а изменяя лишь ток в его обмотке. Но что чтобы вызвать ЭДС индукции в одной катушке за счет изменения тока в другой, совершенно не обязательно вставлять одну из них внутрь другой, а можно расположить их рядом И в этом случае при изменении тока в одной катушке возникающий переменный магнитный поток будет пронизывать (пересекать) витки другой катушки и вызовет в ней ЭДС. Кроме того, величина ЭДС взаимоиндукции зависит от величины индуктивности обеих катушек и от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Следовательно, различные по своей индуктивности и взаимному расположению катушки и в различной среде способны вызывать одна в другой различные по величине ЭДС взаимоиндукции. Чтобы иметь возможность различать между собой различные пары катушек по их способности взаимно индуктировать ЭДС, введено понятие о взаимоиндуктивности или коэффициенте взаимоиндукции. Обозначается ся взаимоиндуктивность буквой М. Единицей ее измерения, так же как и индуктивности, служит генри. Генри — это такая взаимоиндуктивность двух катушек, при которой изменение тока в одной катушке на 1 ампер в 1 секунду вызывает в другой катушке ЭДС взаимоиндукции, равную 1 вольту. На величину ЭДС взаимоиндукции влияет магнитная проницаемость окружающей среды. Чем больше магнитная проницаемость среды, по которой замыкается переменный магнитный поток, связывающий катушки, тем сильнее индуктивная связь катушек и больше величина ЭДС взаимоиндукции. На явлении взаимоиндукции основана работа такого важного электротехнического устройства, как трансформатор. 20. Энергия магнитного поля. ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней. Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. И эту формулу можно вывести. Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить: 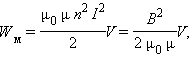 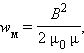 А это объемная плотность энергии магнитного поля, и она справедлива для всех магнитных полей(а не ток для соленоида). А это объемная плотность энергии магнитного поля, и она справедлива для всех магнитных полей(а не ток для соленоида).21. Микро- и макротоки. Магнитные моменты атомов. Элементарная теория диа- и парамагнетизма. Механизмы намагничивания. Интенсивность намагничивания. Магнетиками называются вещества, способные приобретать во внешнем магнитном поле собственное магнитное поле, т. е., намагничиваться. Магнитные свойства вещества определяются магнитными свойствами электронов и атомами (молекулами ) вещества. Магнитные свойства различных веществ весьма разнообразны. Все магнетики принято делить на три класса: 1) парамагнетики – вещества, которые слабо намагничиваются в магнитном поле, причем результирующее поле в парамагнетиках сильнее, чем в вакууме, магнитная проницаемость парамагнетиков m > 1; Такими свойствами обладают алюминий, платина, кислород и др.; 2) диамагнетики – вещества, которые слабо намагничиваются против поля, то есть поле в диамагнетиках слабее, чем в вакууме, магнитная проницаемость m < 1. К диамагнетикам относятся медь, серебро, висмут и др.; 3) ферромагнетики – вещества, способные сильно намагничиваться в магнитном поле, . Это железо, кобальт, никель и некоторые сплавы. При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки: Макротоки– упорядоченное движение заряженных частиц, при котором частицы перемещаются на расстояния, много большие межмолекулярных . Микротоки – движение заряженных частиц внутри атомов и молекул. 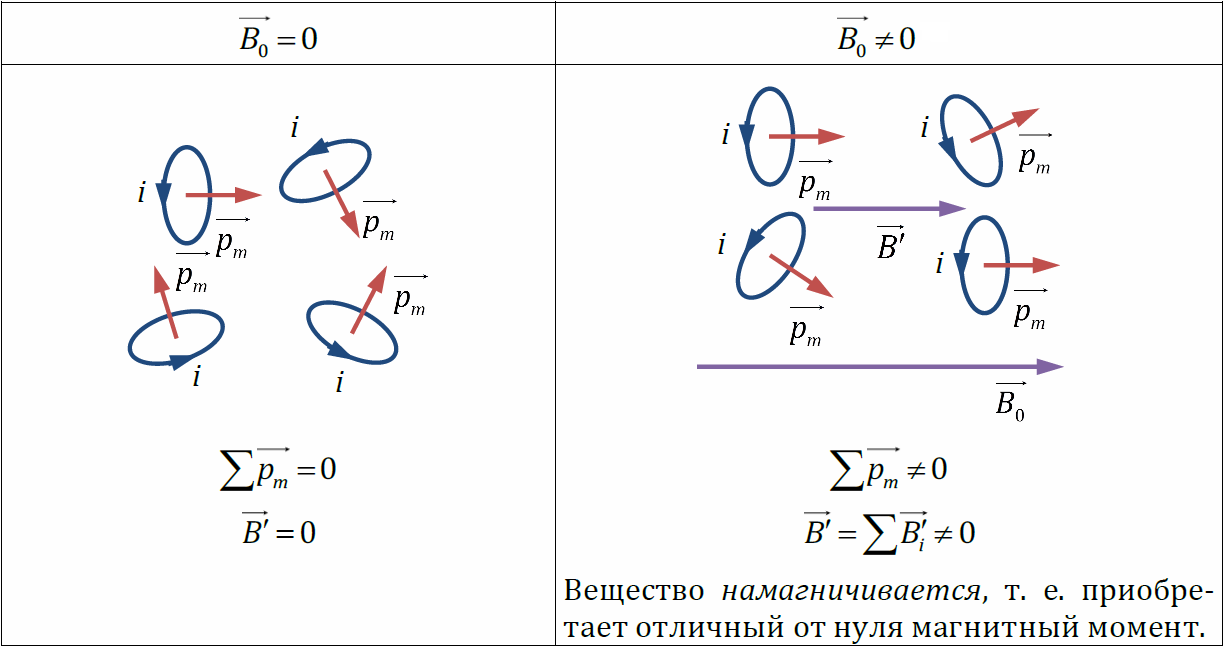 Магнитное поле в веществе определяется полем макротоков и усреднённым полем микротоков: Каждый электрон в атоме (молекуле), двигаясь вокруг ядра, создаёт микроток и собственное магнитное поле; это движение характеризуется микротоком i и магнитным моментом pm . В отсутствие внешнего магнитного поля (макротоков) все магнитные моменты атомов ориентированы разнонаправленно и 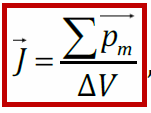 Намагниченность – векторная характеристика магнитного поля в веществе, равная дипольному моменту вещества, занимающего единичный объём. Намагниченность – векторная характеристика магнитного поля в веществе, равная дипольному моменту вещества, занимающего единичный объём.Теорема о циркуляции J Проведём внутри вещества (магнетика) замкнутый контур L (РИС.А) и подсчитаем сумму микротоков, сцепленных с этим контуром. Рассмотрим элемент контура L длиной Δl(РИС. Б). Центры микротоков, сцепленных с участком Δl, находятся внутри цилиндра длины Δlи площади основания, равной площади S микротоков. Основание этого цилиндра параллельно плоскостям микротоков и составляет угол α с участком Δl. Объём этого цилиндра где n – концентрация магнетика – число микротоков (молекул), находящихся в веществе единичного объёма. Сумма микротоков, сцепленных с участком Δl, pm– магнитный момент молекулы. Просуммируем эти выражения при , т. е. проинтегрируем по всему контуру L. – теорема о циркуляции намагниченности: циркуляция вектора намагниченности по произвольному замкнутому контуру равна сумме микротоков, сцепленных с этим контуром. 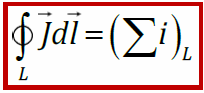 22. Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля. Магнитная проницаемость среды. Вывод закона полного тока для магнитного поля в веществе. Напряженность магнитного поля и ее связь с вектором магнитной индукции. Магнитная восприимчивость и магнитная проницаемость среды. 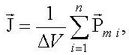 При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоки– упорядоченное движение заряженных частиц, при котором частицы перемещаются на расстояния, много большие межмолекулярных. Микротоки– движение заряженных частиц внутри атомов и молекул. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего или собственного, магнитного поля, создаваемого микротоками.Характеризует магнитное поле в веществе вектор , равный геометрической сумме Ввнеш и Ввнутрмагнитных полей:В = Ввнеш + Ввнутр. При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоки– упорядоченное движение заряженных частиц, при котором частицы перемещаются на расстояния, много большие межмолекулярных. Микротоки– движение заряженных частиц внутри атомов и молекул. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего или собственного, магнитного поля, создаваемого микротоками.Характеризует магнитное поле в веществе вектор , равный геометрической сумме Ввнеш и Ввнутрмагнитных полей:В = Ввнеш + Ввнутр.Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность, равная отношению магнитного момента малого объема вещества к величине этого объема: 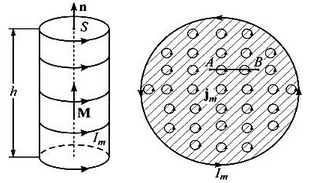 Для того чтобы связать вектор намагниченности среды с током, рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S. Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала повсюду постоянна. Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки. В местах соприкосновения отдельных атомов и молекул молекулярные токи противоположно направлены и компенсируют друг друга. Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток, возбуждающий во внешнем пространстве магнитное поле, равное полю, созданному всеми молекулярными токами. 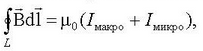 Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе. где Iмакро и Iмикро – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L. Вклад вIмикро дают только те молекулярные токи, которые нанизаны на замкнутый контур L.Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе. где Iмакро и Iмикро – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L. Вклад вIмикро дают только те молекулярные токи, которые нанизаны на замкнутый контур L.Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением  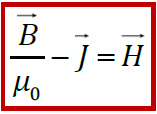 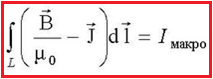 Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность натянутую на этот контур. Вектор Называется напряженностью магнитного поля. 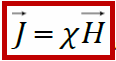 Намагниченность изотропной среды с напряженностью связаны соотношением:где χ – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением Намагниченность изотропной среды с напряженностью связаны соотношением:где χ – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением -относительная магнитная проницаемость вещества. В вакууме μ = 1. -относительная магнитная проницаемость вещества. В вакууме μ = 1.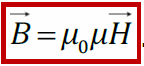 |

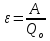
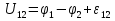
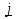
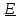
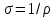
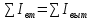
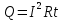
 а
а 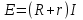 тогда
тогда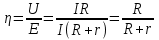 где r - внутр сопротивление источника тока
где r - внутр сопротивление источника тока  , где Т - термодинамическая температура. Согласно опытным данным, R
, где Т - термодинамическая температура. Согласно опытным данным, R