эл ток. шпора эл ток. Р ассмотрим проводящую среду с одним типом свободных носителей заряда, в которой существует ток
 Скачать 105.2 Kb. Скачать 105.2 Kb.
|
|
Характеристики электрического тока. Связь плотности тока с концентрацией и скоростью упорядоченного движения свободных носителей заряда Электрический ток - упорядоченное движение носителей заряда. Для существования электрического тока необходимо наличие в среде свободных носителей заряда и сил, приводящих эти носители в упорядоченное движение. За направление тока принимается направление упорядоченного движения положительно заряженных носителей. При напряженности поля, равной нулю (E ⃗= 0 ), имеет место только хаотичное движение зарядов, связанное с их тепловым движением. При напряженности поля, не равной нулю (E ⃗ ≠ 0) на хаотическое движение зарядов накладывается их упорядоченное движение. Линиями тока называются траектории упорядоченного движения зарядов. Если через некоторую поверхность S за время dt проходит заряд dq, то силой тока через поверхность S называют величину I=dq/( dt). Плотностью тока называют отношение силы тока dl через элементарную площадку dS⊥, перпендикулярную линиям тока, к ее площади: j=dI/(dS )=dq/(dt*dS) Р Пусть q+ – величина заряда одного носителя, n+ – концентрация носителей (число носителей в единице объема), υ+ – средняя скорость упорядоченного движения носителей. Рассмотрим в этой среде элементарную трубку тока в форме прямого цилиндра площадью dS⊥ и длиной υ+ dt, где dt – время, за которое весь заряд, находящийся внутри этой трубки, пересечет площадку dS⊥. Элементарная трубка тока настолько мала по длине и площади поперечного сечения, что в пределах неё плотность тока можно считать одинаковой. Заряд, находящийся внутри этой трубки, равен dq= q+ n+ dV , где dV = υ+ dtdS⊥ – объем элементарной трубки тока. Следовательно, j = q+ n+ υ+ – плотность тока в случае одного типа свободных носителей тока. Для двух типов: j = q+ n+ υ++ |q-| n- υ- – плотность тока для двух типов свободных носителей зарядов Необходимые условия существования постоянного электрического тока в замкнутой цепи. Падение напряжения. ЭДС необходимыми условиями существования тока в замкнутой цепи являются, во-первых, наличие свободных носителей заряда, во-вторых, существование электрического поля, приводящего носители в упорядоченное движение и, в-третьих, наличие источника сторонних сил. Рассмотрим участок проводника, на котором действуют сторонние и кулоновские силы. П  усть усть 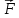 стор– результирующая всех сторонних сил, действующих на свободный заряд q на участке цепи от (⋅)1 до (⋅)2, стор– результирующая всех сторонних сил, действующих на свободный заряд q на участке цепи от (⋅)1 до (⋅)2, 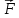 кул – результирующая всех кулоновских сил, действующих на заряд q на этом же участке цепи. Результирующая сила кул – результирующая всех кулоновских сил, действующих на заряд q на этом же участке цепи. Результирующая сила 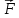 равна равна 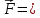 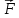 стор стор  . .Величина, равная работе всех сил (кулоновских и сторонних) по перемещению заряда на участке цепи, деленной на величину заряда, называется падением напряжения на этом участке цепи: Закон Джоуля – Ленца Закон Джоуля–Ленца, открытый экспериментальным путем, устанавливает, что количество теплоты, выделение которого сопровождает постоянный ток, пропорционально произведению квадрата силы тока на время его протекания: 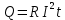 , где где R – коэффициент пропорциональности, который называется сопротивлением проводника и является его характеристикой. В случае, когда сила тока меняется со временем, следует рассмотреть малый промежуток времени dt, в течение которого силу тока можно считать постоянной. При этом выделяется количество теплоты , где где R – коэффициент пропорциональности, который называется сопротивлением проводника и является его характеристикой. В случае, когда сила тока меняется со временем, следует рассмотреть малый промежуток времени dt, в течение которого силу тока можно считать постоянной. При этом выделяется количество теплоты  Отсюда следует, что за промежуток времени Δt = t2 – t1 в проводнике выделяется количество теплоты, равное Отсюда следует, что за промежуток времени Δt = t2 – t1 в проводнике выделяется количество теплоты, равное 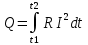 Закон Ома Пусть на рассматриваемом участке цепи не совершается механическая работа и не происходят химические реакции. Тогда работа результирующей сторонних и кулоновских сил по переносу заряда dq из (⋅)1 в (⋅)2 проводящей среды по закону сохранения энергии равна тепловой энергии, величина которой определяется законом Джоуля– Ленца: U12dq=  . Отсюда U12 . Отсюда U12 U12I=RI2. Таким образом I= U12I=RI2. Таким образом I=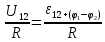 . Это равенство называется законом Ома для неоднородного участка цепи. Для замкнутой цепи, когда ϕ1 = ϕ2, ε12 = ε, приходим к следующему виду закона Ома . Это равенство называется законом Ома для неоднородного участка цепи. Для замкнутой цепи, когда ϕ1 = ϕ2, ε12 = ε, приходим к следующему виду закона Ома  . Для однородного участка цепи ε12 = 0 и закон Ома принимает вид . Для однородного участка цепи ε12 = 0 и закон Ома принимает вид  З  акон Ома в дифференциальной форме. акон Ома в дифференциальной форме.Рассмотрим элементарную трубку тока в однородной проводящей среде и применим к ней закон Ома для однородного участка цепи:  Последнее - представляет собой закон Ома в дифференциальной форме, который позволяет определять распределение плотности тока, если известна напряженность электрического поля. Из этого закона следует, что в проводнике линии тока совпадают с силовыми линиями электрического поля. Закон Джоуля – Ленца в дифференциальной форме Рассмотрим элементарную трубку тока и применим к ней закон Джоуля–Ленца: Величина 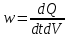 , где dQ – количество теплоты, выделяемое при прохождении тока в объеме проводника dV за время dt, называется удельной мощностью тока. Для удельной мощности тока получим равенство w =σE2 , которое называется законом Джоуля–Ленца в дифференциальной форме. Учитывая закон Ома в дифференциальной форме j= σE= , где dQ – количество теплоты, выделяемое при прохождении тока в объеме проводника dV за время dt, называется удельной мощностью тока. Для удельной мощности тока получим равенство w =σE2 , которое называется законом Джоуля–Ленца в дифференциальной форме. Учитывая закон Ома в дифференциальной форме j= σE=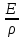 , закон Джоуля–Ленца в дифференциальной форме может быть записан также в виде w = ρj2 . , закон Джоуля–Ленца в дифференциальной форме может быть записан также в виде w = ρj2 . |
