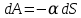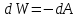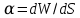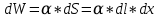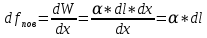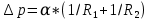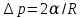Лабораторная работа 16 Определение коэффициента поверхностного натяжения жидкости
 Скачать 1.99 Mb.
|
|
Федеральное государственное учреждение высшего профессионального образования «Ковровская государственная технологическая академия имени В.А. Дегтярёва» Кафедра ПМ и САПР Лабораторная работа № 1.16 «Определение коэффициента поверхностного натяжения жидкости» Цель работы: Измерение коэффициента поверхностного натяжения воды. Задания к работе: n= 8,tºC= 22º К работе допущен: Работу выполнил: Работу защитил: Ковров 2018 Введение Молекулы жидкости взаимодействуют между собой с силами притяжения на расстоянии, равном нескольким эффективным диаметрам молекулы, т.е. величине порядка 10-9 м. Это расстояние является радиусом молекулярного действия r. Сфера радиуса r называется сферой молекулярного действия. Таким образом, каждая молекула испытывает притяжение со стороны всех молекул, находящихся внутри сферы молекулярного взаимодействия, центр которой совпадает с центром рассматриваемой молекулы. Для молекул М1, находящихся от поверхности жидкости на расстоянии  r, результирующая сила притяжения к соседним молекулам в среднем равно нулю (рис.1).Иначе обстоит дело, если молекула находится на расстоянии от поверхности, меньшем r. В этом случае часть сферы молекулярного действия, выступающая над поверхностью жидкости, заполнена молекулами пара и воздуха. Так как плотность газообразной сферы над поверхностью жидкости многократно меньше плотности жидкости, то на молекулы, находящиеся в поверхностном слое, например, молекулы М2 и М3 (рис. 1), действует равнодействующая сила fравн, направленная внутрь жидкости перпендикулярно к поверхности. Модуль этой силы растет при переходе от внутренней к наружной границе слоя.  Рис.1 Схема для объяснения свойств поверхностного слоя жидкости Переход молекулы из глубины жидкости на поверхность приводит к увеличению площади поверхности на величину dS и сопровождается работой против равнодействующей силы:
Коэффициент ɑ - является основной величиной, характеризующей свойства поверхности жидкости, и называется коэффициентом поверхностного натяжения (ɑ>0) . Он численно равен работе, совершаемой молекулами, переходящими из глубины поверхности за единицу. В системе СИ - [ɑ]=Дж/м2. Работа молекулы, переходящей из глубины жидкости в поверхностный слой, совершается за счет ее кинетической энергии и идет на увеличение ее потенциальной энергии. Таким образом, молекулы в поверхностном слое обладает избыточной потенциальной энергией по сравнению с молекулами внутри жидкости:
Эта избыточная потенциальная энергия есть свободная энергия поверхностного слоя. Таким образом, из (1) и (2) следует, что коэффициент поверхностного натяжения можно определить как свободную энергию единицы площади поверхностного слоя жидкости:
где 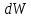 - свободная энергия поверхности жидкости.Если на поверхности жидкости мысленно провести замкнутый контур и удалить поверхностные молекулы за пределами этого контура, то для того, чтобы при этом форма контура не изменилась в соответствии с принципом Лагранжа, к контуру следует приложить эквивалент действия удаленных поверхностных молекул. Таким эквивалентом являются силы притяжения между поверхностными молекулами, направленные по касательной к поверхности жидкости (рис.2). Эти силы называются силами поверхностного натяжения.                            Рис.2. Участок поверхности жидкости на котором показаны силы поверхностного натяжения, действующие на замкнутый контур. Вывод молекул из глубины жидкости на поверхность, ограниченную контуром, приводит к перемещению границы контура на величину dx. Если контур разбить на элементарные участки dl, то перемещение каждого такого участка на dxприведет к увеличению площади поверхности жидкости, ограниченной контуром, на dS. Такое увеличение поверхности приведет к увеличению свободной энергии, потенциальной по своей сути, как следует из (3), на величину:
В этом случае модуль силы поверхностного натяжения с учетом (4) можно определить из связи между консервативной силой и потенциальной энергией:
Из (5) коэффициент поверхностного натяжения можно определить как физическую величину, численно равную силе поверхностного натяжения, действующей на единице длины линии, мысленно проведенной на поверхности жидкости. В этом случае единица измерения коэффициента поверхностного натяжения в системе СИ - [ɑ] = Н/м. Коэффициент поверхностного натяжения вызывают дополнительное избыточное давление в жидкости в случае, если ее поверхность является плоской. Так как в равновесии свободная энергия поверхности стремится к минимуму, то и поверхность жидкости стремится к наименьшей в данных условиях площади, что приводит к появлению положительного избыточного давления (∆p>0) в случае выпуклой поверхности (рис. 3,а) и отрицательного избыточного давления (∆p<0) в случае выгнутой поверхности (рис. 3,б).  Рис.3. Избыточное давление под выпуклой поверхностью (а) и избыточное давление под выгнутой поверхностью (б) Величина избыточного давления ∆p определяется формулой Лапласа:
где R1 и R2 - радиусы кривизны поверхностности в двух взаимно перпендикулярных сечениях. Для сферической поверхности R1=R2. Избыточное давление в соответствии с (6) определяется по формуле:
Существует ряд методов определения коэффициента поверхностного натяжения жидкостей: метод отрыва капель, метод отрыва кольца от поверхности жидкости, капиллярный метод, метод наибольшего давления в пузырьке газа и др. Описание установки В настоящей работе коэффициент поверхностного натяжения определяется методом наибольшего давления в пузырьке газа. Этот метод реализуется в экспериментальной установке, схема которой представлена на рис. 4.  Она состоит из двух сообщающихся сосудов 1 и 2, соединенных между собой внизу трубкой 3, вверху – трубкой 4 с калиброванным капилляром и трубкой 5 и с краном 6, расположенной выше торца калиброванного капилляра 7 и уровня жидкости. Сосуд 1 соединяется трубкой 8 с атмосферой. Заполнение установки исследуемой жидкостью осуществляется через воронку 9 с краном 10. Принцип действия установки заключается в следующем. При перетекании жидкости из сосуда 2 в сосуд 1 жидкость из сосуда 1 вытесняет воздух через калиброванный капилляр трубки 4, на срезе которого формируется и срывается в пузырек воздуха. Давление необходимое для этого процесса, обеспечивается перепадом гидростатических давлений жидкости в первом и втором сосудах. Выходу воздуха из капилляра препятствует гидростатическое давление жидкости на глубине h и лапласово давление на срезе капилляра. Образование и отрыв пузырьков воздуха прекращается при равенстве давления воздуха на выходе капилляра p1 максимальному давлению воздуха в пузырьке p2:  |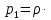
