ЛАБОРАТОРНАЯ РАБОТА № 179 АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЛАБОРАТОРНАЯ РАБОТА.179 (2). Лабораторная работа 179 адиабатический процесс политропический процесс
 Скачать 142 Kb. Скачать 142 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 179 АДИАБАТИЧЕСКИЙ ПРОЦЕССПОЛИТРОПИЧЕСКИЙ ПРОЦЕСС Ознакомьтесь с теорией в конспекте и учебнике (Савельев, т. 1, § 82, 97). Запустите программу. Выберите «Термодинамика и молекулярная физика», «Адиабатический процесс». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна. ЦЕЛЬ РАБОТЫ: Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе. Экспериментальное подтверждение закономерностей адиабатического процесса. Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели. Ознакомление с основами анализа и моделирования термодинамических процессов в идеальных газах. Определение молярной теплоемкости в политропических процессах идеального газа. Определение показателя адиабаты и работы газа в политропическом процессе. КРАТКАЯ ТЕОРИЯ: СОСТОЯНИЕ системы имеет фиксированные значения макроскопических параметров, описывающих систему в целом. Параметры, характеризующие систему в целом, называются ПАРАМЕТРАМИ СОСТОЯНИЯ. Примерами являются температура, давление, объем и т. д. РАВНОВЕСНЫМ называется такое состояние системы, при котором все параметры системы имеют определенные значения, остающееся неизменными сколь угодно долго при неизменных внешних условиях. ОБРАТИМЫМ называется процесс, при реализации которого в обратном направлении система проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Равновесные процессы всегда обратимы. КРУГОВЫМ процессом (ЦИКЛОМ) называется процесс, при котором система после ряда изменений возвращается в исходное состояние. УРАВНЕНИЕ СОСТОЯНИЯ идеального газа (уравнение Менделеева–Клапейрона) 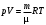 . .ТЕПЛОЕМКОСТЬ тела численно равна отношению количества тепла ∂Q, сообщенного телу, к изменению температуры тела dT, которое при этом произошло: СТЕЛА = 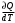 . .УДЕЛЬНОЙ теплоемкостью вещества называется отношение теплоемкости к массе тела. Если тело не меняет свой объем, то оно не совершает работы, поэтому при постоянном объеме тела переданное телу тепло ∂Q идет на изменение его внутренней энергии dU. ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ОБЪЕМЕ: СV = 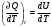 . .ТЕПЛОЕМКОСТЬ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ идеального газа, молекулы которого имеют i степеней свободы CP = 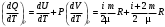 (1). (1).ОТНОШЕНИЕ 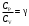 является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты. является константой (в определенном диапазоне температур) для данного газа. Эта константа называется показателем адиабаты.Формула 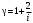 (2) устанавливает связь отношения теплоемкостей с числом степеней свободы молекулы газа i. (2) устанавливает связь отношения теплоемкостей с числом степеней свободы молекулы газа i.ЧИСЛО (количество) СТЕПЕНЕЙ СВОБОДЫ есть минимальное количество независимых координат, необходимых для однозначного описания положения молекулы в пространстве ИЛИ минимальное количество независимых движений, суперпозиция которых дает любое движение молекулы. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ всегда дает 3 степени свободы. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2 степени свободы для линейной молекулы и 3 степени свободы, если атомы в молекуле не расположены на одной линии. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ дает 2nКОЛ степеней свободы, где nКОЛ – количество независимых колебаний атомов в молекуле (у двухатомной молекулы nКОЛ = 1). АДИАБАТИЧЕСКИМ называется процесс, происходящий без теплообмена с внешней средой (∂Q = 0). Уравнение адиабаты: PV = const (3). Принято также выделять ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и ИЗОХОРИЧЕСКИЙ процессы. ПОЛИТРОПНЫМ называется процесс, в котором молярная теплоемкость С остается постоянной. Уравнение политропического процесса имеет вид: рV n = const, (1) где n = 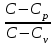 . (2) . (2)МОЛЯРНОЙ ТЕПЛОЕМКОСТЬЮ называется физическая величина С, численно равная теплоте 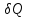 , которую нужно сообщить одному молю вещества для изменения его температуры на 1 К в рассматриваемом термодинамическом процессе: , которую нужно сообщить одному молю вещества для изменения его температуры на 1 К в рассматриваемом термодинамическом процессе:С = 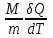 , (3) , (3)где M – молярная масса, m – масса газа. Выражение (3) теперь можно записать в форме 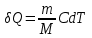 . (4) . (4)или в интегральной форме 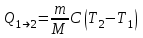 . .Таким образом, если количество тепла, полученное в некотором термодинамическом процессе 12 при m = const, прямо пропорционально разности температур 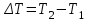 , то теплоемкость газа постоянна и процесс является политропическим. , то теплоемкость газа постоянна и процесс является политропическим. 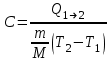 . . ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для любого равновесного процесса изменения состояния идеального газа имеет вид 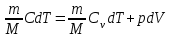 . (5) . (5)Тогда из уравнения (5) имеем: C = Cv + 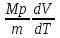 . (6) . (6)Связь между объемом газа и его температурой в политропном процессе можно найти из выражения (1) и уравнения Клапейрона–Менделеева 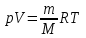 : :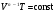 . .Дифференцируя последнее выражение, получим: 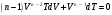 , ,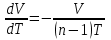 . .Тогда уравнение (6) примет вид: 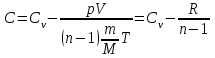 . .Учитывая, что 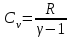 , где , где 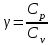 – показатель адиабаты, получим: – показатель адиабаты, получим: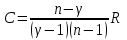 , , или 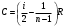 . (7) . (7)Таким образом, если термодинамический процесс идеального газа действительно является политропным, то есть молярная теплоемкость в ходе процесса не изменяется, то ее величина рассчитывается по формуле (7). В настоящей работе используется модель одноатомного газа (i = 3), поэтому в политропных процессах при n = 1 согласно выражению (7) молярная теплоемкость С должна быть равна 16,6 Дж/мольК, а при n = 2 C = 15,2 Дж/мольК. Частными случаями политропного процесса являются: изотермический: n = 1, C = ; изобарический: n = 0, C = Cp; изохорический: n = , С = Сv; адиабатический: n = , где = 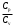 , С = 0. , С = 0.МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ Внимательно рассмотрите картинку на рисунке, найдите рисунок элемента, в котором реализуется адиабатический процесс, обратите внимание на его теплоизоляцию. Найдите математическую формулировку условия теплоизоляции. Ознакомьтесь с графиками в правой части изображения. Зарисуйте необходимое в свой конспект лабораторной работы. Получите у преподавателя допуск для выполнения измерений. 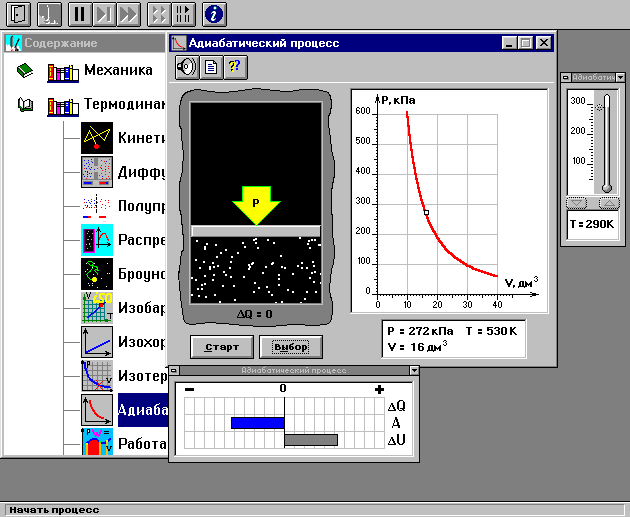 ИЗМЕРЕНИЯ: Установите начальное значение объема Vнач = 40 дм3 и начальную температуру Т1 газа, близкую к числам из табл. 1. Для этого нажмите кнопку «ВЫБОР», переместите маркер мыши так, чтобы его острие находилось в указанной точке вблизи границы столбика на градуснике, и нажмите и удерживая левую кнопку мыши двигайте столбик. Нажмите мышью кнопку «Старт» на экране и наблюдайте перемещение поршня на левой картинке модели и перемещение точки по красной кривой теоретической адиабаты. Попробуйте останавливать процесс нажатием кнопки «СТОП». Последующий запуск процесса осуществляется нажатием кнопки «Старт». После автоматической остановки процесса запустите его снова, нажав кнопку «Старт», и останавливайте, нажимая кнопку «Стоп», когда крестик на теоретической адиабате (красная кривая) будет находиться вблизи следующих значений объема: 15, 20, 25, 30, 35 и 40 дм3 (6 значений), записывая при остановке значения объема, температуры и давления в табл. 2. Установите новое значение температуры Т2, взяв его из табл. 1, задавая Vнач = 40 дм3 и повторите измерения, записывая результаты в табл. 3. ТАБЛИЦА 1. Начальные значения температуры (не перерисовывать)
ТАБЛИЦЫ 2, 3 Результаты измерений
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА: Постройте на одном рисунке графики экспериментальных зависимостей логарифма давления от логарифма объема для обеих адиабат (указав на них начальные температуры). Для каждой адиабаты определите по графику экспериментальное значение показателя, используя формулу 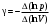 . .Определите число степеней свободы молекулы газа, исследуемого в данной компьютерной модели, используя формулу (2). Подберите распространенный газ, структура молекулы которого близка к наблюдаемой. Запишите ответы и проанализируйте ответы и графики. 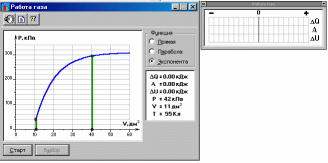 В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Прямая». Подведите маркер мыши к выделенной левой точке графика р = f(V) на экране монитора, нажмите левую кнопку мыши, и, удерживая ее в нажатом состоянии, переместите начало графика в точку с координатами (Р1, V1, Т1), взятыми из табл. 1 для вашей бригады. Аналогичным образом переместите выделенную крайнюю правую точку графика в точку с координатами (Р20, V20). На мониторе щелкните мышью кнопкув верхнем ряду кнопок, а в нижней части экрана кнопку «СТАРТ». Нажмите два раза кнопку в верхнем ряду кнопок и запишите в первый столбец таблицы два значения 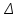 Q и Т. Q и Т.Последовательно повторяя действия п. 5 20 раз, заполните табл. 2. В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Парабола», проделайте измерения п. 2–6 и запишите результаты опытов в табл. 3. В прямоугольном окошке «Функция» нажмите маркером мыши кнопку «Экспонента», проделайте измерения п. 2–6 и запишите результаты опытов в табл. 4. ТАБЛИЦА 1. Начальные и конечные параметры для трех термодинамических процессов
ТАБЛИЦЫ 2, 3, 4. Результаты измерений температуры и количества выделения тепла в ходе термодинамического процесса расширения газа Табл. 2, функция «прямая» Табл. 3, функция «парабола» Табл. 4, функция «экспонента»
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА 1.Вычислите и запишите во вторую строку таблиц 2, 3, 4 разности температур Ti T1. На миллиметровой бумаге или на листе в клетку формата А4 постройте по экспериментальным точкам графики в виде линейной зависимости 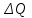 от разности температур Ti T1 для трех исследуемых процессов. (Каждый график на отдельном листе!) от разности температур Ti T1 для трех исследуемых процессов. (Каждый график на отдельном листе!)По тангенсу угла наклона прямой линии графика к оси разности температур, используя формулу 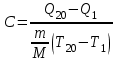 , определите молярную теплоемкость политропического процесса и сравните ее с теоретическим значением, рассчитанным по формуле (7). , определите молярную теплоемкость политропического процесса и сравните ее с теоретическим значением, рассчитанным по формуле (7). Рассчитайте работу газа в этих процессах по формуле 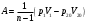 и сравните эти значения со значениями, указанными в нижнем окне монитора при p20 и V20. Проанализируйте полученные результаты , сделайте оценку погрешности измерений. Вопросы и задания для самоконтроля Что такое параметры состояния системы? Дайте определение равновесного состояния системы. Какой процесс называется обратимым? Что такое цикл? Что такое уравнение состояния? Для какого физического газа можно применить модель «идеальный газ»? Какому уравнению подчиняется состояние идеального газа? Напишите его. Дайте определение теплоемкости тела. Дайте определение удельной теплоемкости. Напишите формулу для теплоемкости при постоянном объеме. Напишите формулу для теплоемкости идеального газа при постоянном давлении. Что такое число степеней свободы? Чему оно равно для одноатомной молекулы? Что такое показатель адиабаты? Напишите формулу связи показателя адиабаты с числом степеней свободы молекулы идеального газа. Дайте определение адиабатического процесса. Напишите уравнение адиабатического процесса. Дайте определение изопроцесса. Перечислите известные изопроцессы. Напишите уравнение и нарисуйте PV-диаграмму изотермического процесса. Напишите уравнение и нарисуйте PV-диаграмму изобарического процесса. Напишите уравнение и нарисуйте PV-диаграмму изохорического процесса. Сформулируйте закон Больцмана о равнораспределении энергии по степеням свободы молекул. Почему колебательная степень свободы молекулы обладает вдвое большей энергией, чем поступательная и вращательная? В чем состоит качественная неравноценность между работой и теплообменом как формами передачи энергии? Что такое внутренняя энергия идеального газа? В результате каких процессов может изменяться внутренняя энергия идеального газа? Что называется молярной теплоемкостью газа? Почему Cv больше, чем Cp? Покажите применение первого начала термодинамики к изопроцессам в идеальных газах. Чему равна работа изобарного расширения моля идеального газа при нагревании на 1 К? Чему равна работа изохорного расширения моля газа при нагревании на 1 К? Нагревается или охлаждается идеальный газ, если он расширяется при постоянном давлении? Температура газа в сосуде постоянна. Запишите на основе первого начала термодинамики соотношение между сообщенным количеством теплоты и совершенной работой. Газ переходит из одного и того же состояния 1 в одно и тоже состояние 2 в результате следующих процессов: 1) изотермического; 2) изобарного; 3) изохорного; 4) адиабатного. Рассмотрев эти процессы графически, показать: 1) в каком процессе работа расширения максимальна? 2) в каком случае газу сообщается большее количество тепла? Какой процесс называется политропным? Показатель политропы n 1. Нагревается или охлаждается идеальный газ при сжатии? Определите, больше или меньше нуля молярная теплоемкость газа в термодинамическом процессе 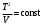 , если а) газ одноатомный; 2) газ двухатомный. , если а) газ одноатомный; 2) газ двухатомный. |
