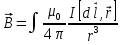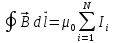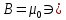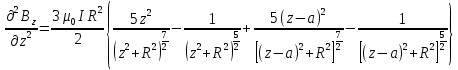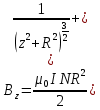№18 Иссл магнитного поля катушек Гельмгольца. Лабораторная работа 18 исследование магнитного поля катушек гельмгольца
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Лабораторный вариант 02.02.2023 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский горный университет» Кафедра общей и технической физики общая физика Лабораторная работа № 18 ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ КАТУШЕК ГЕЛЬМГОЛЬЦА Методические указания к лабораторной работе САНКТ-ПЕТЕРБУРГ 2023 Цель работы – изучение магнитных полей токов различной конфигурации, изучение принципа суперпозиции, изучение системы, позволяющие создавать в пространстве однородные магнитные поля (катушек Гельмгольца). ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Магнитное поле в вакуумеДвижущиеся заряды (проводники с токами) изменяют свойства окружающего их пространства – создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды действуют силы. Силовую характеристику магнитного поля называют магнитной индукцией и обозначают как 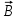 . Единица измерений магнитной индукции в СИ – тесла [Тл]. . Единица измерений магнитной индукции в СИ – тесла [Тл].Опыт показывает, что магнитное поле имеет направленный характер, поэтому индукция магнитного поля – векторная величина. Для магнитного поля справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности, т.е.  (1) (1)Ж. Био и Ф. Савар провели в 1820 г. исследование магнитных полей токов различной формы. Они установили, что магнитная индукция во всех случаях пропорциональна силе тока, создающей магнитное поле, и зависит от расстояния до той точки, в которой определялась величина вектора 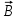 . .П. Лаплас проанализировал экспериментальные данные, полученные Ж. Био и Ф. Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока. Магнитная индукция поля, создаваемого элементом тонкого проводника с током Iи длиной dl(рис. 1), определяется выражением (2):  (2) (2)где μ0 – магнитная постоянная (μ0= 4π.10-7Гн/м),  – вектор, совпадающий с элементарным участком тока и направленный по току, – вектор, совпадающий с элементарным участком тока и направленный по току,  – радиус-вектор, проведенный от токового элемента в точку P, в которой определяется поле – радиус-вектор, проведенный от токового элемента в точку P, в которой определяется поле  Рис. 1. Магнитная индукция от элемента проводника с током Проинтегрировав формулу (2) по всем элементам, П. Лаплас пришел к выражению для результирующего поля всего проводника:
Формула (3) является одним из аналитических выражений закона Био – Савара – Лапласа. Поле вектора 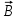 можно представить наглядно с помощью линий магнитной индукции, которые проводятся так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора можно представить наглядно с помощью линий магнитной индукции, которые проводятся так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора 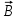 , а густота линий соответствовала модулю этого вектора в данном месте. , а густота линий соответствовала модулю этого вектора в данном месте.Исходя из закона Био – Савара – Лапласа можно доказать, что циркуляция вектора 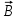 по произвольному замкнутому контуру Г равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром, т.е. по произвольному замкнутому контуру Г равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром, т.е.
Г Выражение (4) справедливо только для поля в вакууме. Вычисляя сумму токов в правой части уравнения (4), положительным нужно считать ток, направление которого связано с направлением обхода по контуру правилом правого винта. Выражение (4) называют теоремой о циркуляции вектора 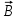 . Тот факт, что циркуляция вектора . Тот факт, что циркуляция вектора 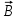 не равна нулю, означает, что магнитное поле не потенциально. Такое поле называют вихревым. не равна нулю, означает, что магнитное поле не потенциально. Такое поле называют вихревым.Соленоидом называется цилиндрическая катушка с обмоткой (провод, навитый на цилиндрический каркас). Внутри длинного соленоида, с отношением длины соленоида к его диаметру не меньше 10, магнитное поле однородно и его индукция равна
где n– число витков соленоида, приходящееся на единицу его длины, I– сила тока в соленоиде. Близкое к однородному магнитное поле может быть создано также с помощью катушек Гельмгольца. Катушками Гельмгольца называется система, состоящая из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу. В пространстве между катушками создается почти однородное магнитное поле, и его индукцию можно рассчитать по формуле:
где N– число витков в каждой катушке, I– сила тока, проходящего через последовательно соединенные катушки, R– средний радиус катушки. В лабораторной установке исследуется магнитное поле катушек Гельмгольца. Для измерения магнитной индукции используется датчик на основе эффекта Холла. Магнитное поле катушек Гельмгольца Получим приведенную выше формулу (6) магнитной индукции в центре катушек Гельмгольца. Рассмотрим сначала магнитное поле, создаваемое током, протекающим по тонкому проводу, имеющем форму окружности радиуса R(круговой ток). Найдем магнитную индукцию 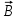 на оси кругового тока на расстоянии zот центра контура (рис. 2). Элемент тока на оси кругового тока на расстоянии zот центра контура (рис. 2). Элемент тока  создает в точке А согласно закону Био – Савара – Лапласа индукцию, модуль которой равен создает в точке А согласно закону Био – Савара – Лапласа индукцию, модуль которой равен
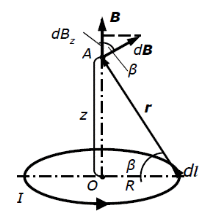 Рис. 2. Поле кругового тока От всех элементов тока будет образовываться конус векторов d 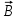 . Из соображений осевой симметрии можно заключить, что результирующий вектор . Из соображений осевой симметрии можно заключить, что результирующий вектор 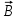 в точке А будет направлен по оси zвверх. Это значит, что для нахождения модуля этого вектора необходимо сложить проекции векторов d в точке А будет направлен по оси zвверх. Это значит, что для нахождения модуля этого вектора необходимо сложить проекции векторов d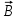 на ось z: на ось z:
Интегрируя выражение (7) по всему токовому контуру и учитывая, что  , получим , получим
Формула (8) определяет величину магнитной индукции на оси кругового тока. Рассмотрим далее систему из двух кольцевых проводников одинакового радиуса R, соосно расположенных на оси zна расстоянии а друг от друга. Поместим начало координат в центре одного из колец (рис. 3). Если токи в каждом кольце одинаково направлены и равны по величине, то индукция магнитного поля в точке А на расстоянии zот первого кольца равна сумме магнитных индукций полей, создаваемых токами первого 1 и второго 2 колец. Согласно формуле (8) имеем:
Тогда индукция магнитного поля на оси колец в точке с координатой zравна
г  де I– сила тока в каждом кольце, R – радиус кольца. де I– сила тока в каждом кольце, R – радиус кольца.Рис. 3. Поля кольцевых проводников Неоднородность Bzв первом приближении характеризуется первой производной
При  получаем получаем 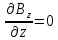 . Найдем вторую производную: . Найдем вторую производную:
В точке c  вторая производная вторая производная  обращается в нуль при условии, что a = R. обращается в нуль при условии, что a = R.Условия обращения в нуль выражений (10) и (11) позволяют утверждать, что для получения наилучшей однородности поля расстояние между кольцами должно равняться их радиусу. Два коаксиальных кольцевых проводника одинакового радиуса, расположенные в параллельных плоскостях, расстояние между которыми равно радиусу колец, называют кольцами Гельмгольца. Магнитное поле на оси колец Гельмгольца вблизи точки 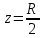 обладает высокой степенью продольной однородности. Можно также показать, что высокая однородность поля будет и в поперечном направлении. Таким образом, поле однородно в значительной части объема пространства между кольцами Гельмгольца. обладает высокой степенью продольной однородности. Можно также показать, что высокая однородность поля будет и в поперечном направлении. Таким образом, поле однородно в значительной части объема пространства между кольцами Гельмгольца.Графически результат сложения магнитных полей на оси колец Гельмгольца показан на рис. 4.  Рис. 4. Распределение магнитных полей между кольцами Гельмгольца На рисунке представлены графики изменения B1zи B2z(в условных единицах) магнитных полей на оси каждого из колец Гельмгольца, а также суммарное поле Bzна оси системы колец.  На рис.5 изображены силовые линии магнитного поля колец Гельмгольца. Показаны лишь линии, лежащие в одной из плоскостей, проходящей через ось системы колец. Подобная картина имеет место в любой из этих плоскостей. Рис. 5. Силовые линии от колец Гельмгольца Данный результат получен для двух тонких колец с током. На практике такую систему колец использовать нельзя, так как величина тока, необходимая для получения даже небольших полей будет слишком велика. Поэтому для получения однородных полей используют катушки с большим числом витков, которые называют катушками Гельмгольца. Катушки должны выполняться так, чтобы размеры сечения катушек были малы по сравнению с их средним радиусом. Расстояние между катушками, отсчитываемое от их центров, равно среднему радиусу катушек. Несмотря на конечный размер сечения катушек, высокая степень однородности магнитного поля сохраняется в большом объеме пространства между катушками Гельмгольца. Если катушка имеет Nвитков и по ней течет ток I, то формула (8) может быть записана в виде
а формула (9) может быть записана для двух катушек с током, соединенных последовательно, усиливающих поля друг друга и находящихся на расстоянии а друг от друга в виде
При встречном включении катушек их магнитные поля противоположно направлены и поэтому в формуле (13) вместо знака плюс должен быть - минус:
Из формулы (13) следует, что если a<R, то индукция магнитного поля на оси катушек имеет максимальное значение. Если a>R, то индукция магнитного поля имеет минимальное значение. В этом можно убедиться, выполнив эксперимент. Для катушек Гельмгольца (а = R) в средней точке ( 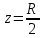 ) по формуле (13) получим ) по формуле (13) получим
Неточность калибровки датчика Холла и невозможность правильной установки геометрических параметров при выполнении эксперимента приводит к отклонению реальных результатов от расчетных примерно на 0,15 мТл. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ Описание экспериментальной установкиРабота выполняется на установке, разработанной и созданной фирмой PHYWE (Германия). В состав установки входит следующее оборудование (рис. 6): пара одинаковых катушек Гельмгольца (Dср = 400 мм, N=154); универсальный регулируемый источник питания постоянного тока; датчик Холла; линейка для измерения расстояний.  Рис. 6. Экспериментальная установка Короткие соосные катушки расположены на расстоянии а =R(радиус катушек R= 200 мм) друг от друга и включены последовательно, образуя магнитную систему, известную как катушки Гельмгольца. Катушки (1к и 2к) питаются от регулируемого источника (0 - ± 8 В, 0 - 2 А), работающего в режиме стабилизации по току (рис. 7).   Рис. 7. Схема подключения катушек Гельмгольца  Порядок выполнения работы1. Исследование магнитного поля короткой катушки на ее оси при постоянной силе тока 1.1. Включить приборы. 1.2. В качестве исследуемого объекта вначале использовать одну из катушек, подключив ее к источнику тока. 1.3. Установить силу тока, равную нулю, путем регулировки выхода силы тока на источнике. 1.4. Регуляторами грубой 1 и тонкой настройки 2 (рис. 8) добиться нулевых показаний тесламетра. 1.5. Установить держатель с измерительным щупом и линейку в удобном для считывания положении. Следить при установке и в процессе измерений за параллельностью между щупом и линейкой. 1.6. Расположить катушку таким образом, чтобы датчик Холла находился в центре витков катушки. Для этого использовать зажимно–регулировочный винт по высоте на держателе измерительного щупа. Плоскость катушки должна быть перпендикулярна щупу. 1.7. Убедиться, что за время прогрева тесламетра, его показания остались нулевыми. Если это не выполнено – установить нулевые показания тесламетра при нулевом токе в катушке. 1.8. Установить силу тока в короткой катушке 2А (путем регулировки выхода на источнике питания). 1.9. Измерить магнитную индукцию Bэксп на оси катушки z в зависимости от расстояния до центра катушки. Для этого смещать держатель измерительного щупа по направлению линейки, сохраняя параллельность своему первоначальному положению. Принять z=0 в центре плоскости катушки. Данные занести в таблицу 1. Таблица1. Зависимость магнитной индукции на оси короткой катушки от расстояния до центра катушки
2. Исследование магнитного поля короткой катушки в ее центре в зависимости от силы тока 2.10. Повторить пункты 1.2 – 1.7. 2.11. Измерить зависимость индукции в центре катушки от силы тока, проходящей через нее. Данные занести в таблицу 2. Таблица2. Зависимость магнитной индукции в центре короткой катушки от силы тока в ней.
3. Изучение принципа суперпозиции и исследование магнитного поля катушек Гельмгольца 3.1. Повторить пункты 1.2 – 1.7. 3.2. Соединить катушки последовательно (см. рис. 7) так, чтобы при прочих равных условиях магнитное поле двух катушек стало больше, чем от одной катушки, исследованной выше. Последовательное соединение катушек обеспечивается соединением клемм №1 катушек №1 и №2 между собой в конфигурации, указанной на рисунке. Клеммы №2 катушек соединены с блоком питания. 3.3. Установить силу тока 2 А. 3.4. Измерить магнитную индукцию в пространстве между катушками как функцию координаты z, приняв за начало отсчета центр одной из катушек. 3.5. Данные занести в табл. 3. Таблица 3. Значения индукции магнитного поля в мТл в пространстве между катушками Гельмгольца по оси z.
4. Исследование магнитного поля катушек Гельмгольца в зависимости от силы тока 4.1. Повторить пункт 3.2. 4.2. Измерить зависимость индукции в центре между катушками (z=a/2) от силы тока, проходящей через них. Данные занести в таблицу 4. Таблица4. Зависимость магнитной индукции в центре между катушками Гельмгольца от силы тока в них.
Обработка результатов экспериментаДля одной катушки (табл. 1) построить в одних координатных осях график измеренной экспериментальной зависимости Bэксп(z)и теоретическую зависимость Bтеор(z), рассчитанную по формуле (12). Проанализировать полученные зависимости. По данным таблицы 2 построить теоретическую и экспериментальную зависимости магнитной индукции в центре короткой катушки от силы тока в ней. Теоретическую и экспериментальную зависимости построить в одних координатных осях. Проанализировать полученные зависимости. Для системы катушек Гельмгольца построить экспериментальную зависимость Bэксп(z) и теоретическую зависимость Bтеор(z), рассчитанную по формуле (13). Проанализировать полученные зависимости. По данным таблицы 4 построить теоретическую и экспериментальную зависимости магнитной индукции в центре между катушками Гельмгольца от силы тока в них. Теоретическую и экспериментальную зависимости построить в одних координатных осях. Проанализировать полученные зависимости. Контрольные вопросыЧто называется индукцией магнитного поля и в каких единицах она измеряется? Как создать однородное магнитноеполе? Чему равна индукция магнитного поля внутри длинногосоленоида? Пользуясь законом Био – Савара – Лапласа получите формулу для индукции магнитного поля на оси кругового витка стоком. Что называется кольцами Гельмгольца? Чему равна индукция магнитного поля на оси колец Гельмгольца? Как устроена система катушек Гельмгольца? Чему равна индукция магнитного поля в центре катушек Гельмгольца? Почему индукция магнитного поля на оси двух одинаковых соосных катушек с током имеет минимум, если расстояние между катушками больше их радиуса? 10. Какая сила действует на движущийся заряд в однородном магнитном поле? 11. В чем заключается эффект Холла? 12. Как эффект Холла используется для измерения индукции магнитного поля? ТРЕБОВАНИЯ К СОДЕРЖАНИЮ ОТЧЁТА ПО ЛАБОРАТОРНОЙ РАБОТЕОтчёт оформляется в печатном виде на листах формата А4 в соответствии с указанными ниже требованиями. Помимо стандартного титульного листа в содержании отчёта должны быть раскрыты пункты, перечисленные ниже. 1. Цель работы. 2. Краткое теоретическое содержание. 1) Явление, изучаемое в работе. 2) Определения основных физических понятий, объектов, процессов и величин. 3) Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы. 4) Пояснения к физическим величинам и их единицы измерений. 3. Схема установки. 4. Расчётные формулы. 5. Формулы для расчёта погрешностей косвенных измерений. 6. Таблицы с результатами измерений и вычислений. (Таблицы должны иметь номер и название. Единицы измерения физических величин должны быть указаны в отдельной строке таблицы под строкой с обозначениями физических величин.) 7. Пример вычисления (для одного опыта). 1) Исходные данные. 2) Вычисления. 3) Окончательный результат. 8. Графический материал. 1) Записать аналитическое выражение функциональной зависимости, которая представлена на графике. 2) На осях координат указать масштаб, физические величины и единицы измерения. 3) На координатной плоскости должны быть нанесены экспериментальные точки. 4) По результатам эксперимента, представленным на координатной плоскости, провести плавную линию, аппроксимирующую функциональную теоретическую зависимость в соответствии с методом наименьших квадратов. 9. Анализ полученного результата. Выводы. ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ 1. Графики строятся с использованием компьютера. 2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х), значения функции - на оси ординат (ось у). 3. Из экспериментальных данных определить пределы изменения аргумента и функции. 4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин. 5. На осях координат указать масштаб (при очень больших или очень малых величинах, показательную часть в записи величины указать рядом с единицами измерений на оси). 6. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой). 7. Провести через экспериментальные точки плавную линию, в соответствии с выбранной аппроксимирующей (приближающей) функцией, описывающей зависимость между величинами, полученными в результате экспериментальных измерений. (Определение параметров приближающей функции выполняется одним из наиболее распространённых математических методов - методом наименьших квадратов. В компьютерной программе Еxcel реализация метода осуществляется при использовании режима линии тренда и выбранного вид аппроксимирующей функции.) РЕКОМЕНДАЦИИ ПО ЗАЩИТЕ ОТЧЕТАК защите допускаются студенты, подготовившие отчет в соответствии с требованиями к его содержанию в установленные сроки. После проверки преподавателем содержания отчёта, при наличии ошибок и недочетов, работа возвращается студенту на доработку. При правильном выполнении лабораторной работы, соблюдении всех требований к содержанию и оформлению отчёта, студент допускается к защите. Для успешной защиты отчета необходимо изучить теоретический материал по теме работы, а так же освоить математический аппарат, необходимый для вывода расчётных формул работы. При подготовке к защите, помимо данного методического пособия, необходимо использовать учебники и другие учебные пособия, рекомендованные к учебному процессу кафедрой ОТФ. Во время защиты студент должен уметь ответить на вопросы преподавателя в полном объёме теоретического и методического содержания данной лабораторной работы, уметь самостоятельно вывести необходимые расчётные формулы, выполнить анализ полученных зависимостей и прокомментировать полученные результаты библиографический список учебной литературы Мартинсон Л.К., Морозов А.Н., Смирнов Е.В. Электромагнитное поле: Учеб. пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана,2013.Савельев И.В. Курс общей физики: Учебное пособие для втузов. В 5 кн. Кн. 2: Электричество и магнетизм. – М.: Изд-во Астрель – АСТ, 2001. Матвеев А.Н. Электричество и магнетизм. – М.: Оникс 21 век,2005. |