ТЭЦ - Лабораторная. 17 ТЭЦ лабораторная 19 (1). Лабораторная работа 19 Исследование на эвм распределения напряжения в длинных линиях
 Скачать 409.4 Kb. Скачать 409.4 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ) Кафедра теории электрических цепей Лабораторная работа №19 «Исследование на ЭВМ распределения напряжения в длинных линиях» Выполнил студент группы ******* _______________ *************** Проверил _________________ ********** Москва 2008 Цель работыС помощью машинного эксперимента исследовать распределение напряжений вдоль однородной длинной линии передачи при различных значениях сопротивлений нагрузки. Предварительные расчеты Длина линии без потерь равна l = 160 м, погонная емкость C0 = 100 пФ/м, погонная индуктивность L0 = 0,25 мкГн. Рассчитать: волновое сопротивление ZВ; фазовую скорость VФ; время запаздывания t3; частоту генератора f, при которой на линии укладывается одна длина волны; период колебаний генератора T.  Рисунок 1 Полученные данные записать в таблицу 1. Увеличить длину линии до l = 400 м. Произвести аналогичный расчет, и полученные данные занести в таблицу 1. // Расчеты выполнены в программе Scilab 6.1.0 // Лабораторная работы № 19 // Выполнил студент группы ******************* // Длина линии без потерь l, м l = 160; // Погонная емкость C0, Ф/м C0 = 100*10^-12; // Погонная индуктивность L0, Гн/м L0 = 0.25*10^-6; // Фазовая скорость Vf, м/c Vf = 1/sqrt(L0*C0) Vf = 2.000D+08 // Волновое сопротивление Zv, Ом Zv = sqrt(L0/C0) Zv = 50. // Время запаздывания сигнала t3, c t3 = l/Vf t3 = 0.0000008 // Частота, при которой на линии укладывается одна длина волны f = Vf/l f = 1250000. // Период колебаний T и частота f связаны соотношением, с T = 1/f T = 0.0000008 // Расчеты при l = 400 м l = 400; // Фазовая скорость Vf, м/c Vf = 1/sqrt(L0*C0) Vf = 2.000D+08 // Волновое сопротивление Zv, Ом Zv = sqrt(L0/C0) Zv = 50. // Время запаздывания сигнала t3, c t3 = l/Vf t3 = 0.000002 // Частота, при которой на линии укладывается одна длина волны f = Vf/l f = 500000. // Период колебаний T и частота f связаны соотношением, с T = 1/f T =
0.000002 Результаты вычислений представлены в таблице 1. Таблица 1 Рассчитать и построить кривые распределения действующих значений напряжения вдоль линии для режима холостого хода (ХХ) RH = ꝏ. При расчетах принять U2 = 1 B, l = 160 м, y ϵ [0; l]. На полученном графике обозначьте характерные точки (0, λ/4, λ/2, 3λ/4 и λ). Рассчитать коэффициент бегущей волны (КБВ) и коэффициент отражения ρ. Полученные данные записать в таблицы 2 и 3. Для режима холостого хода (ХХ) 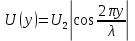 ; λ = l ; λ = l// Напряжение U, B U2 = 1; // Длина линии l, м l = 160; // Расчет кривых распределения действующих значений напряжения for yi = 0:10:l Uxx(i) = U2*abs(cos(2*%pi*yi/l)); i = i + 1; end Uxx' ans = column 1 to 9 1. 0.9238795 0.7071068 0.3826834 6.123D-17 0.3826834 0.7071068 0.9238795 1. column 10 to 17 0.9238795 0.7071068 0.3826834 1.837D-16 0.3826834 0.7071068 0.9238795 1. plot(y,Uxx) xgrid() xtitle('Кривая распределения действующих значений напряжения','y,м','|U(y)|,B (XX)') Рассчитаем КБВ и коэффициент отражения ρ. 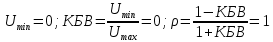 ; ;Кривая распределения действующих значений напряжения вдоль линии для режима холостого хода (ХХ) изображена на рисунке 2.       0 λ Рисунок 2 3λ/4 λ/4 λ/2  Рассчитать и построить кривые распределения действующих значений напряжения вдоль линии для режима короткого замыкания (КЗ) RH = 0. При расчетах принять I2 = 1 A, l = 160 м, y ϵ [0; l]. На полученном графике обозначьте характерные точки (0, λ/4, λ/2, 3λ/4 и λ). Рассчитать коэффициент бегущей волны (КБВ) и коэффициент отражения ρ. Полученные данные записать в таблицы 2 и 3. Для режима короткого замыкания (КЗ) 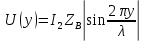 ; λ = l ; λ = l// Сила тока I, A I2 = 1; // Волновое сопротивление Zv, Ом Zv = 50; // Длина линии l, м l = 160; // Расчет кривых распределения действующих значений напряжения y = 0:10:l; i = 1; for yi = 0:10:l Ukz(i) = I2*Zv*abs(sin(2*%pi*yi/l)); i = i + 1; end Ukz' ans = column 1 to 9 0. 19.134172 35.355339 46.193977 50. 46.193977 35.355339 19.134172 6.123D-15 column 10 to 17 19.134172 35.355339 46.193977 50. 46.193977 35.355339 19.134172 1.225D-14 plot(y,Ukz) xgrid() xtitle('Кривая распределения действующих значений напряжения','y,м','|U(y)|,B (КЗ)') Рассчитаем КБВ и коэффициент отражения ρ. 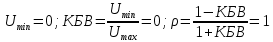 ; ;      Рисунок 3 3λ/4 λ/2 λ/4 λ 0 К  ривая распределения действующих значений напряжения вдоль линии для режима короткого замыкания (КЗ) изображена на рисунке 3. Рассчитать и построить кривые распределения действующих значений напряжения вдоль линии для режима согласованной нагрузки (СН) RH = ZB. При расчетах принять U2 = 1 A, l = 160 м, y ϵ [0; l]. На полученном графике обозначьте характерные точки (0, λ/4, λ/2, 3λ/4 и λ). Рассчитать коэффициент бегущей волны (КБВ) и коэффициент отражения ρ. Полученные данные записать в таблицы 2 и 3. Для режима согласованной нагрузки (СН) 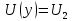 ; λ = l ; λ = lU(y) = U2, Ɐ y ϵ [0; l]. Рассчитаем КБВ и коэффициент отражения ρ.  ; ;Кривая распределения действующих значений напряжения вдоль линии для режима короткого замыкания (КЗ) изображена на рисунке 4. plot(y,[1]) xgrid()       3λ/4 λ/2 λ/4 Рисунок 4 λ 0 x 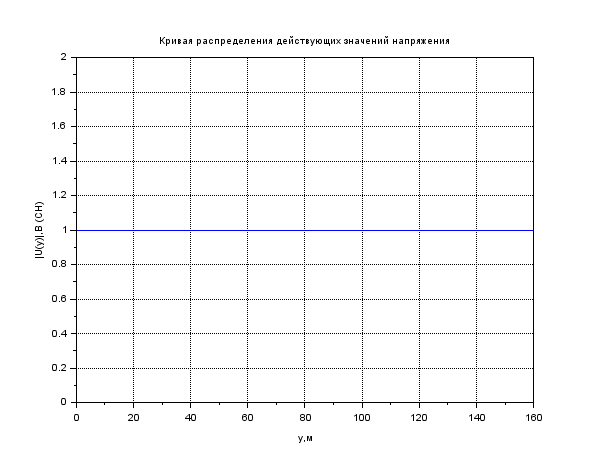 title('Кривая распределения действующих значений напряжения','y,м','|U(y)|,B Рассчитать и построить кривые распределения действующих значений напряжения вдоль линии для режима несогласованной нагрузки (НН) RH = 2ZB. При расчетах принять U2 = 1 A, l = 160 м, y ϵ [0; l]. На полученном графике обозначьте характерные точки (0, λ/4, λ/2, 3λ/4 и λ). Рассчитать коэффициент бегущей волны (КБВ) и коэффициент отражения ρ. Полученные данные записать в таблицы 2 и 3. Для режима согласованной нагрузки (НН): 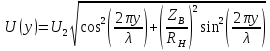 ; λ = l ; λ = l// Волновое сопротивление Zv, B Zv = 50; // Сопротивление нагрузки Rn, Ом Rn = Zv*2 Rn = 100. // Напряжение U, B U2 = 1; // Длина линии l, м l = 160; y = 0:10:l; // Расчет кривых распределения действующих значений напряжения i=1; for yi = 0:10:l > Unn(i) = U2*sqrt((cos(2*%pi*yi/l)^2) + ((Zv/Rn)^2)*(sin(2*%pi*yi/l)^2)); > i = i + 1; > end Unn' ans = column 1 to 9 1. 0.9434856 0.7905694 0.5998624 0.5 0.5998624 0.7905694 0.9434856 1. column 10 to 17 0.9434856 0.7905694 0.5998624 0.5 0.5998624 0.7905694 0.9434856 1. xgrid() xtitle('Кривая распределения действующих значений напряжения','y,м','|U(y)|,B (НН)') Рассчитаем КБВ и коэффициент отражения ρ. 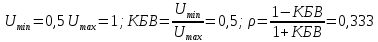 ; ;Кривая распределения действующих значений напряжения вдоль линии для режима короткого замыкания (КЗ) изображена на рисунке 5. plot(y,Unn) xgrid() xtitle('Кривая распределения действующих значений напряжения','y,м','|U(y)|,B (НН)') 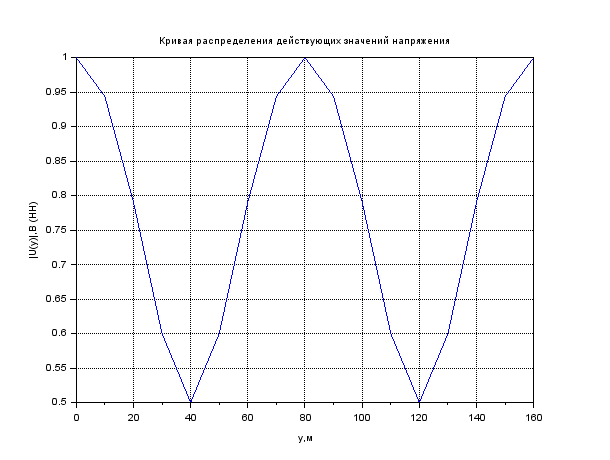       3λ/4 λ/2 λ/4 Рисунок 4 λ 0 Результаты вычислений представлены в таблицах 2 и 3. Таблица 2
Таблица 3
Машинный эксперимент И 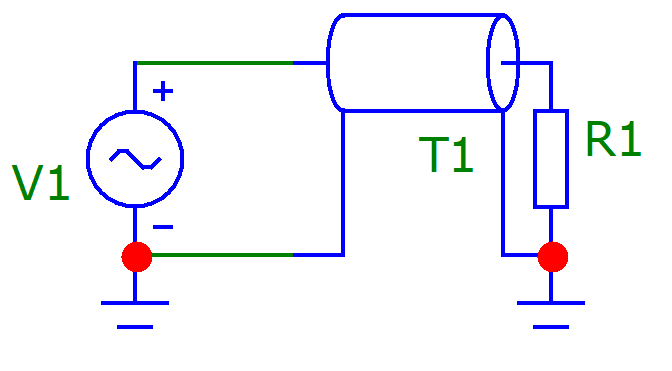 сследуемая схема изображена на рисунке 7. Рисунок 7 Исследование однородной длинной линии передачи U, B  t, c  Рисунок 6 — при l = 160 м t3 = 0,8 мкс U, B  t, c  Рисунок 7 — при l = 400 м t3 = 2 мкс. Увеличение длины линии приводит к увеличению времени задержки. Исследование распределения наложений вдоль линии Для режима холостого хода (ХХ) И 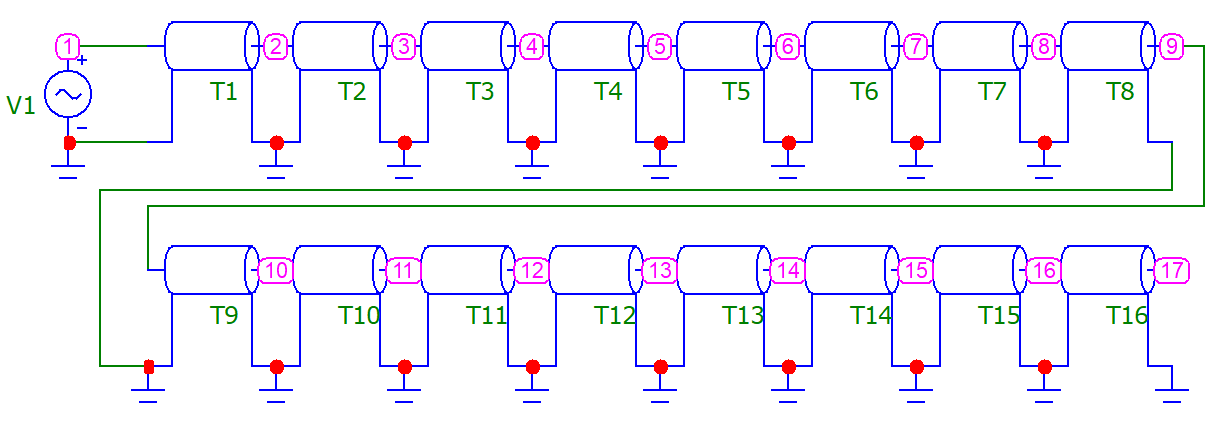 сследуемая схема изображена на рисунке 8. Рисунок 8 Кривая распределения напряжения изображена на рисунке 9. 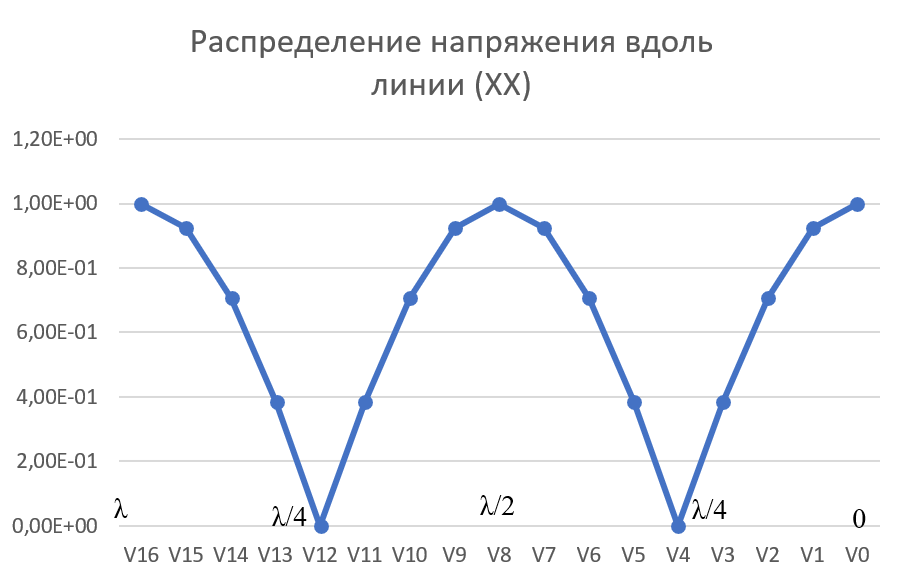 Рисунок 9 Рассчитаем КБВ и коэффициент отражения ρ. 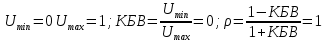 ; ;3.2.2 Для режима короткого замыкания (КЗ) И 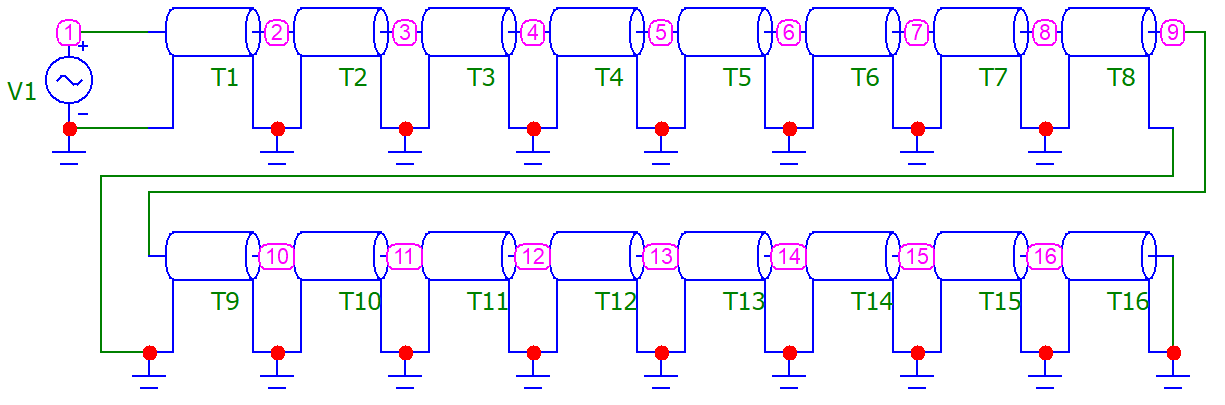 сследуемая схема изображена на рисунке 10. Рисунок 10 К  ривая распределения напряжения изображена на рисунке 11. Рисунок 11 Рассчитаем КБВ и коэффициент отражения ρ. 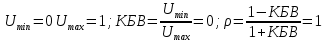 ; ;3.2.3 Для режима согласованной нагрузки (СН) И 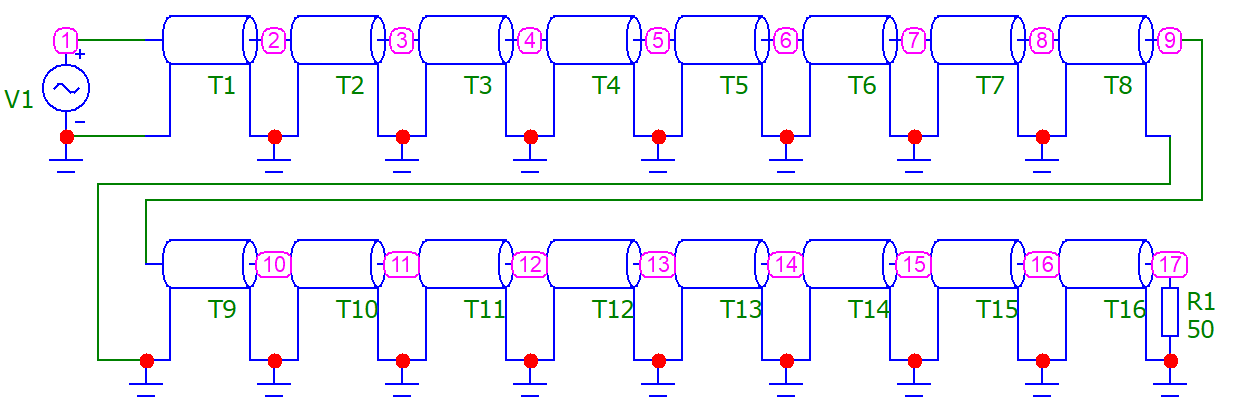 сследуемая схема изображена на рисунке 12. Рисунок 12 Кривая распределения напряжения изображена на рисунке 13. 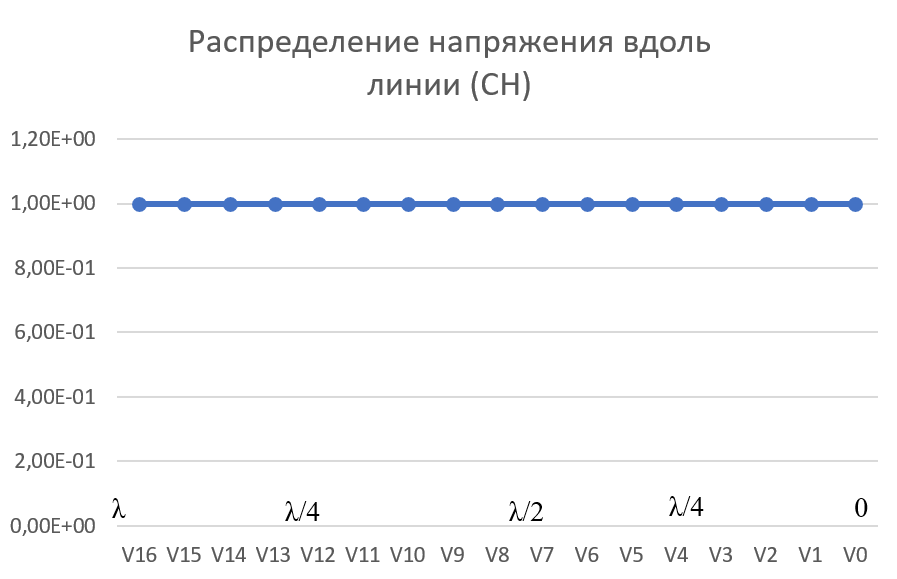 Рисунок 13 Рассчитаем КБВ и коэффициент отражения ρ. 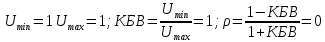 ; ;3.2.4 Для режима несогласованной нагрузки (НН) И  сследуемая схема изображена на рисунке 14. Рисунок 14 К 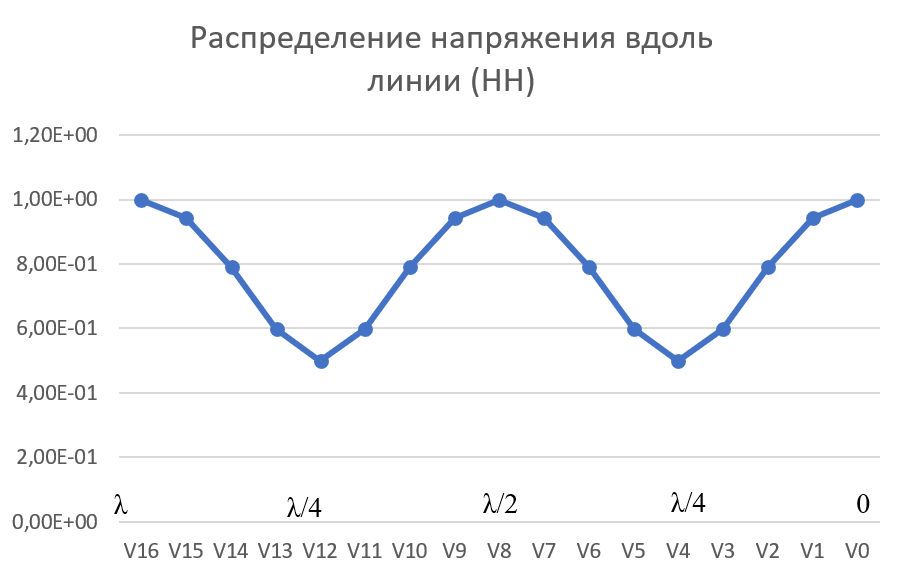 ривая распределения напряжения изображена на рисунке 15. Рисунок 15 Рассчитаем КБВ и коэффициент отражения ρ. 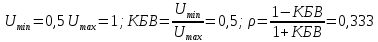 ; ;Вывод: Графики и значения, полученные во время машинного эксперимента, совпадают с графиками и значениями, полученными в предварительных расчетах, значит, предварительные расчеты проведены верно. Контрольные вопросы В каких случаях электрические цепи рассматривают как цепи с распределенными параметрами? Ответ: Когда необходимо учитывать их геометрические параметры. В таких цепях приходится сталкиваться с распределёнными по длине индуктивностями, ёмкостями, резистивными сопротивлениями. Запишите уравнение передачи длинной линии с потерями и без потерь. Ответ: 1) Уравнение передачи длинной линии с потерями: 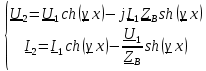 , , 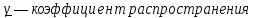 2) Уравнение передачи длинной линии без потерь: 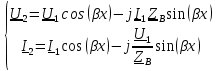 , ,  Что такое волновое сопротивление линии? Ответ: Отношение комплексных напряжения и тока бегущей волны: 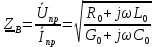 Что называют коэффициентом отражения от нагрузки? Ответ: Отношение комплексной амплитуды отражённой волны к комплексной амплитуде падающей волны.  Какие режимы работы в линии вы знаете? Приведите примеры. Ответ: 1) Режим холостого хода — линия разомкнута на конце, ZH = ꝏ 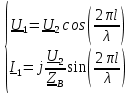 2) Режим короткого замыкания — линия замкнута на конце, ZH = 0 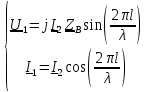 3) Режим работы на согласованную нагрузку, ZH = ZВ 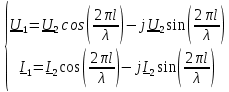 4) Режим работы на несогласованную нагрузку, ZH 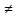 ZВ ZВ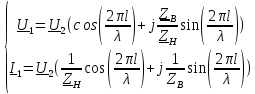 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
