Лабораторная работа 1по Теории Автоматического Управления Примечание
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Лабораторная работа № 1по Теории Автоматического Управления Примечание:Результаты, полученные по каждому пункту задания нужно сразу заносить в отчёт в формате DOC(X) в виде скрин-шотов схем и графиков, при этом схемы (Simulink-модели), соответствующие разным пунктам задания, лучше сохранять в отдельных файлах (с соответствующими именами, например, Model_1_1, Model_1_2, …). Дата рождения: 11.09.2001 Задание: 1. Исследовать в среде MatlabSimulinkзамкнутую систему автоматического регулирования температуры с объектом управления, заданного передаточной функцией что соответствует последовательному соединению апериодического звена 1-го порядка с коэффициентом усиления K = 1,96 и постоянной времени T = 24,451c, и звена чистого запаздывания с временем запаздывания τ = 24c: 1) построить показанную на рисунке схему, настроить все параметры блоков на необходимые значения: 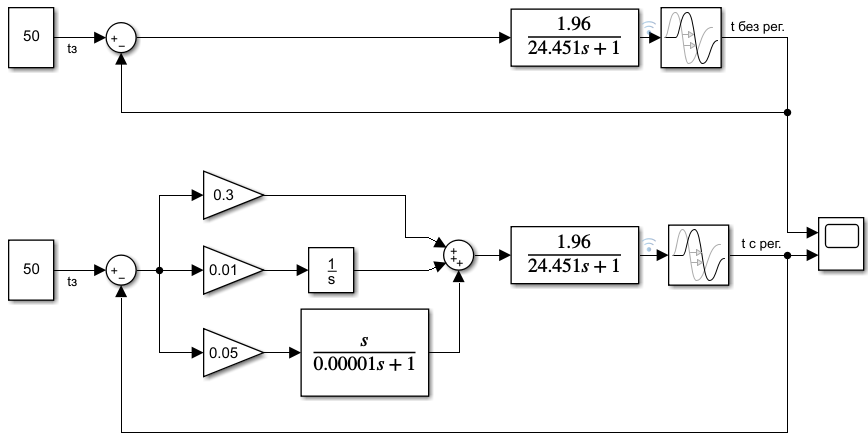 Здесь tз = 50 °С – заданное значение температуры, которое нужно в идеале поддерживать на выходе структурной схемы; Kп = 0,3, Kи = 0,01 и Kд = 0,05 – подобранные вручную коэффициенты соответственно пропорциональной, интегральной и дифференциальной составляющей ПИД-регулятора, при использовании которого получается хороший переходный процесс установления температуры на выходе (нет колебательного процесса и перерегулирования, процесс устанавливается быстро). 2) Получить такие же переходные процессы, как показано на рисунке: 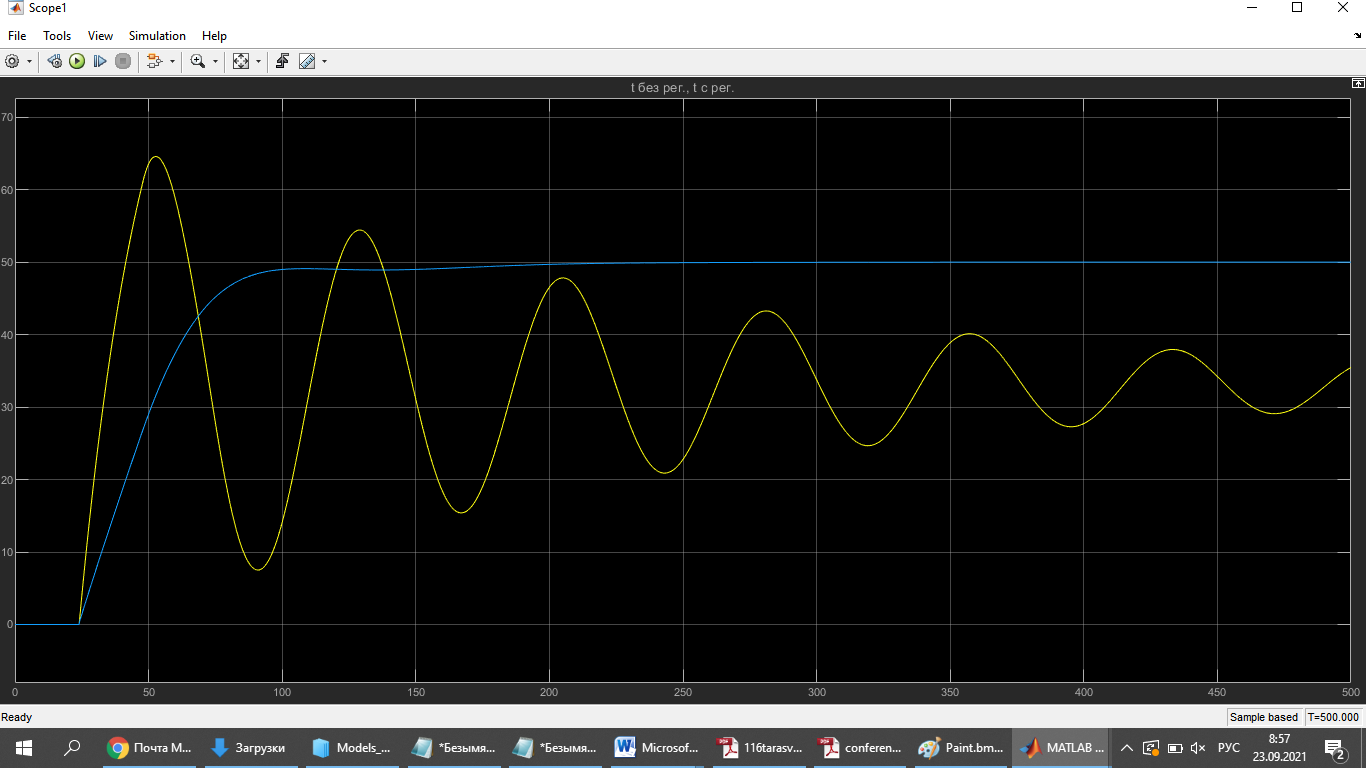 Видно, что процесс без регулятора (жёлтая кривая) очень не хороший: наблюдается сильный колебательный процесс и перерегулирование (температура переваливает выше заданного значения на 15 °С, что соответствует перерегулированию 15/50·100% = 30 %), процесс устанавливается очень долго, и установившееся значение будет равно примерно 35 °С, поэтому имеет место большая ошибка регулирования ε = 50 – 35 = 15 °С. Все указанные недостатки отсутствуют для процесса с использованием правильно настроенного ПИД-регулятора (синяя кривая). Примечание:Если Simulink-модель рассчитывается очень медленно (не за пару секунд) – попробуйте поменять метод расчёта в настройках модели. Выбранный на рисунке метод рассчитывает процессы достаточно быстро. 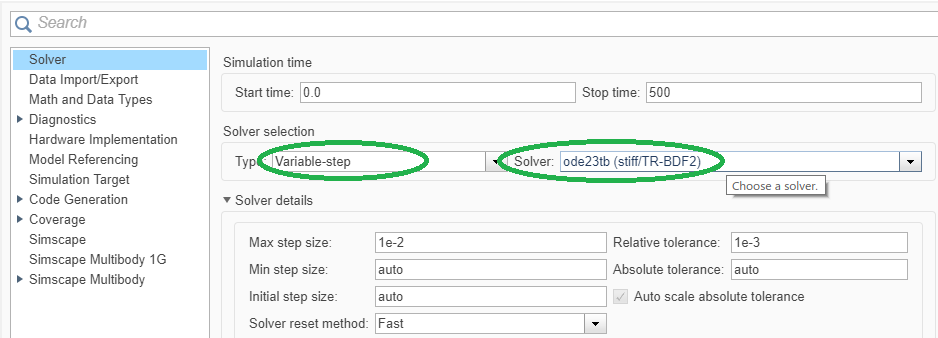 2. Исследовать подобным образом (как в п. 1) объект управления, заданный колебательным звеном 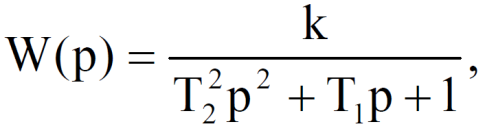 где заданное значение температуры tз(в пределах от 0 до 1000), коэффициент усиления k(в пределах от 1 до 10) и постоянные времени T1 и T2 (в пределах от 1 до 100) нужно задать самим, используя день своего рождения ДД.ММ.(ГГ)ГГ, где ДД – дата, ММ – месяц и ГГ (или ГГГГ) – год рождения студента соответственно(посмотрите, какие числа из даты рождения для каких параметров больше подходят). 1) Отдельно исследовать систему без регулятора: - посмотреть процессы, которые будут при заданном значении температуры tз(скорее всего установившееся значение температуры на выходе будет ниже требуемого значения); - изменить значениеtз до такого значения, чтобы на выходе установившаяся температура была равна заданному в самом начале значению tз (до изменения); если не сможете получить нужного значения температуры – добейтесь хотя бы максимально близкого к нему значения. 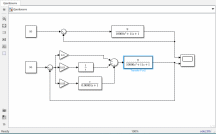 Схема для исследования объекта управления, заданного колебательным звеном (без изменений) 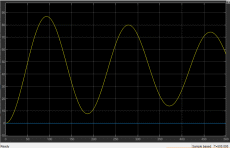 График для исследования объекта управления, заданного колебательным звеном (без изменений) 2) Вернуть исходное значение tз и начать по очереди вводить в систему отдельные части ПИД-регулятора: - при Kи = 0 и Kд = 0 подобрать такое значение Kп , при котором на выходе установившая температура будет равна заданному значениюtз; - (нужно понимать, что если параметры объекта управления немного изменяться, что довольно часто бывает на практике, то настроенный на старый объект управления П-регулятор в новой обстановке будет давать ошибку регулирования)поменять в настроенной системе с П-регулятором какой-нибудь параметр объекта управления (уменьшить или увеличить его в 10 раз) и убедиться, что будет появляться ошибка регулирования; 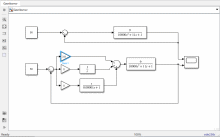 Схема с использованием П–регулятора 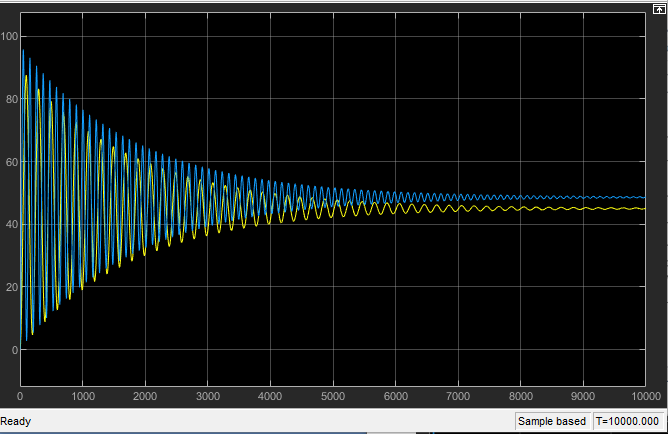 График для случая П –регулятора - вернуть обратно значение изменённого параметра и коэффициента П-регулятора и добавить в регулятор интегральную составляющую (получится ПИ-регулятор) и подобрать такое значение коэффициента Kи, при котором процесс будет стремиться к заданному значению без перерегулирования (возможно, для этого придётся немного изменить значение коэффициентаKп); 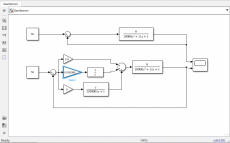 Схема с использованием ПИ–регулятора 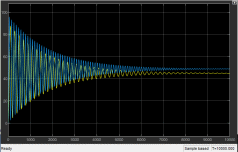 График для случая ПИ–регулятора - добавить к исходному П-регулятору дифференциальную составляющую (получится ПД-регулятор) и подобрать такое значение коэффициента Kд, при котором процессы будут быстро устанавливающимися, желательно без перерегулирования (возможно, для этого придётся немного изменить значение коэффициента Kп); !!! нулевой ошибки регулирования, возможно, не получится добиться; 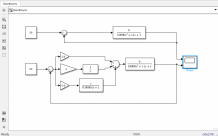 Схема с использованием ПД–регулятора 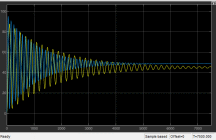 График для случая ПД–регулятора - настроить ПИД-регулятор, подобрав оптимальные значения коэффициентов Kп, Kи и Kд, чтобы получить хорошие процессы (быстрое установление к заданному значению без перерегулирования). 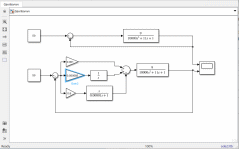 Схема с использованием ПИД–регулятора 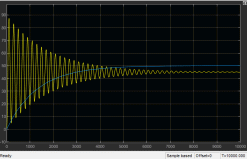 График для случая ПИД–регулятора 3. Настроить сразу ПИД-регулятор, подобрав оптимальные значения коэффициентов Kп, Kи и Kд, чтобы получить хорошие процессы (быстрое установление к заданному значению без перерегулирования), для объекта управления, заданногопередаточной функцией 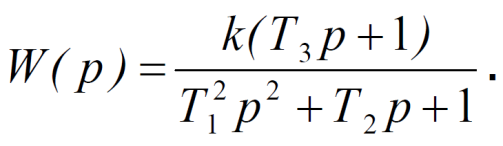 представляющей последовательное соединение колебательного звена (см. п. 2) и форсирующего звена с постоянной времени T3 , значение которой также нужно задать, используя числа из даты рождения студента. Отдельно форсирующее звено с передаточной функцией (T3p+1) будет сложно реализовать, так же, как приходится выкручиваться, чтобы сделать идеальное дифференцирующее звеноpдля добавления дифференцирующей части ПИД-регулятора:p≈p/(0,0001p+1), т.к. в Simulinkневозможно задать передаточную функцию, у которой степень числителя больше степени знаменателя. Поэтому для получения нужной для п. 3 передаточной функцией нужно изменить нужным образом коэффициенты числителя в настройках передаточной функции ранее настроенного колебательного звена. 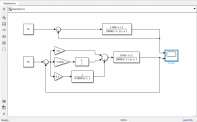 Схема ПИД–регулятора (быстрое установление к заданному значению без перерегулирования) 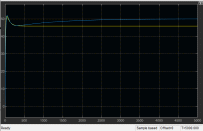 График для случая ПИД-регулятора быстрое установление к заданному значению без перерегулирования) График ПИД–регулятора быстрое установление к заданному значению без перерегулирования) Все рассматриваемые передаточные функции реально соответствуют различным объектам управления, представляющим различные виды нагревателей: п. 1 (апериодическое звено с запаздыванием) – экструдер (например, для нагревания пластика и вытягивания его в виде нити); п. 2 (колебательное звено) – электродный водонагреватель; п. 3 (колебательное + форсирующее звено) –более сложный электродный водонагреватель. |
